2045-到达目的地的第二短时间(Second Minimum Time to Reach Destination)

原文链接: https://leetcode-cn.com/problems/second-minimum-time-to-reach-destination

英文原文

A city is represented as a bi-directional connected graph with n vertices where each vertex is labeled from 1 to n (inclusive). The edges in the graph are represented as a 2D integer array edges, where each edges[i] = [u_i, v_i] denotes a bi-directional edge between vertex u_i and vertex v_i. Every vertex pair is connected by at most one edge, and no vertex has an edge to itself. The time taken to traverse any edge is time minutes.

Each vertex has a traffic signal which changes its color from green to red and vice versa every change minutes. All signals change at the same time. You can enter a vertex at any time, but can leave a vertex only when the signal is green. You cannot wait at a vertex if the signal is green.

The second minimum value is defined as the smallest value strictly larger than the minimum value.

For example the second minimum value of [2, 3, 4] is 3, and the second minimum value of [2, 2, 4] is 4.

Given n, edges, time, and change, return the second minimum time it will take to go from vertex 1 to vertex n.

Notes:

You can go through any vertex any number of times, including 1 and n.
You can assume that when the journey starts, all signals have just turned green.

Example 1:

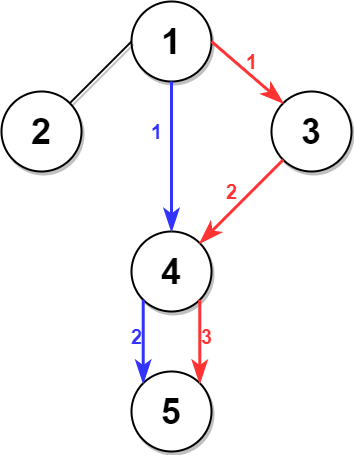
Input: n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
Output: 13
Explanation:
The figure on the left shows the given graph.
The blue path in the figure on the right is the minimum time path.
The time taken is:
- Start at 1, time elapsed=0
- 1 -> 4: 3 minutes, time elapsed=3
- 4 -> 5: 3 minutes, time elapsed=6
Hence the minimum time needed is 6 minutes.

The red path shows the path to get the second minimum time.

Start at 1, time elapsed=0
1 -> 3: 3 minutes, time elapsed=3
3 -> 4: 3 minutes, time elapsed=6
Wait at 4 for 4 minutes, time elapsed=10
4 -> 5: 3 minutes, time elapsed=13
Hence the second minimum time is 13 minutes.

Example 2:

Input: n = 2, edges = [[1,2]], time = 3, change = 2
Output: 11
Explanation:
The minimum time path is 1 -> 2 with time = 3 minutes.
The second minimum time path is 1 -> 2 -> 1 -> 2 with time = 11 minutes.

Constraints:

2 <= n <= 10⁴
n - 1 <= edges.length <= min(2 * 10⁴, n * (n - 1) / 2)
edges[i].length == 2
1 <= u_i, v_i <= n
u_i != v_i
There are no duplicate edges.
Each vertex can be reached directly or indirectly from every other vertex.
1 <= time, change <= 10³

中文题目

城市用一个 双向连通 图表示，图中有 n 个节点，从 1 到 n 编号（包含 1 和 n）。图中的边用一个二维整数数组 edges 表示，其中每个 edges[i] = [u_i, v_i] 表示一条节点 u_i 和节点 v_i 之间的双向连通边。每组节点对由 最多一条 边连通，顶点不存在连接到自身的边。穿过任意一条边的时间是 time 分钟。

每个节点都有一个交通信号灯，每 change 分钟改变一次，从绿色变成红色，再由红色变成绿色，循环往复。所有信号灯都同时改变。你可以在 任何时候 进入某个节点，但是只能在节点 信号灯是绿色时 才能离开。如果信号灯是绿色，你不能在节点等待，必须离开。

第二小的值 是 严格大于 最小值的所有值中最小的值。

例如，[2, 3, 4] 中第二小的值是 3 ，而 [2, 2, 4] 中第二小的值是 4 。

给你 n、edges、time 和 change ，返回从节点 1 到节点 n 需要的 第二短时间 。

注意：

你可以 任意次 穿过任意顶点，包括 1 和 n 。
你可以假设在 启程时 ，所有信号灯刚刚变成绿色。

示例 1：

输入：n = 5, edges = [[1,2],[1,3],[1,4],[3,4],[4,5]], time = 3, change = 5
输出：13
解释：
上面的左图展现了给出的城市交通图。
右图中的蓝色路径是最短时间路径。
花费的时间是：
- 从节点 1 开始，总花费时间=0
- 1 -> 4：3 分钟，总花费时间=3
- 4 -> 5：3 分钟，总花费时间=6
因此需要的最小时间是 6 分钟。

右图中的红色路径是第二短时间路径。
- 从节点 1 开始，总花费时间=0
- 1 -> 3：3 分钟，总花费时间=3
- 3 -> 4：3 分钟，总花费时间=6
- 在节点 4 等待 4 分钟，总花费时间=10
- 4 -> 5：3 分钟，总花费时间=13
因此第二短时间是 13 分钟。

示例 2：

输入：n = 2, edges = [[1,2]], time = 3, change = 2
输出：11
解释：
最短时间路径是 1 -> 2 ，总花费时间 = 3 分钟
最短时间路径是 1 -> 2 -> 1 -> 2 ，总花费时间 = 11 分钟

提示：

2 <= n <= 10⁴
n - 1 <= edges.length <= min(2 * 10⁴, n * (n - 1) / 2)
edges[i].length == 2
1 <= u_i, v_i <= n
u_i != v_i
不含重复边
每个节点都可以从其他节点直接或者间接到达
1 <= time, change <= 10³

通过代码

高赞题解

解题思路

因为是竞赛时候写的，代码比较粗糙。

力扣上的最短路径问题基本上都可以用BFS解决。BFS的队列中我们存两个信息：1. 节点id 2. 到当前节点的时间
这里有两个问题需要处理：

红绿灯等待问题
找的不是最短路；而是第二短的路

第一个问题很好解决：我们知道所有节点都是从绿灯开始，以同样的周期进行红绿灯的交替变换。如果当前时间为 t，一共经历了 t / change 次变化；则 t / change % 2 == 1 则为红灯，否则为绿灯。
如果当前为红灯，我们需要将时间向上取整到当前红灯结束再入队即可。

第二个问题就更简单了，记录多条路径即可。一般的权一样的最短路问题，BFS第一次搜索到终点，即找到了答案。这次我们求第二短的路，记录第二次搜索到的路径即可。可以用两个变量标记一下最短的两条路。因为严格最短，我们需要记录一下具体的值而不是出现次数。同样，一个路径如果经过了两次，我们也不用再把后面的路径加到队列中了。

这里还有一个问题：是否会出现两条不同的路径，长的比短的快呢？答案是不会的，因为红绿灯周期都是一样的，跨越路径的时间也是一样的。

代码如下：

代码

class Solution {
public:
    unordered_map<int, int> fast;
    unordered_map<int, int> second;
    int secondMinimum(int n, vector<vector<int>>& edges, int time, int change) {
        queue<pair<int, int>> Q; // (node, time)
        Q.push(make_pair(1, 0));
        unordered_map<int, vector<int>> G;
        int first = -1;
        
        for (auto edge: edges) {
            if (G.find(edge[0]) == G.end()) G[edge[0]] = vector<int>(0);
            if (G.find(edge[1]) == G.end()) G[edge[1]] = vector<int>(0);
            G[edge[0]].push_back(edge[1]);
            G[edge[1]].push_back(edge[0]);
        }
        
        while(!Q.empty()) {
            pair<int, int> p = Q.front();
            Q.pop();
            int node = p.first;
            int curTime = p.second;
            for (auto next: G[node]) {
                if (next == n) {
                    if (first == -1) {
                        first = curTime + time;
                    } else {
                        if (curTime + time > first) return curTime + time;
                    }
                }
                int targetTime = curTime + time;
                if ((targetTime / change) % 2 == 1) {
                    targetTime = (targetTime / change + 1) * change;
                }
                if (fast.find(next) == fast.end()) {
                    fast[next] = targetTime;
                    Q.push(make_pair(next, targetTime));                
                    continue;
                }
                if (second.find(next) == second.end() && fast[next] < targetTime) {
                    second[next] = targetTime;
                    Q.push(make_pair(next, targetTime));                
                    continue;
                }
            }
        }
        
        return -1;
    }
};

关于我

大家好，我是微扰酱。现在是五道口【悖论13】剧本杀的股东之一，点评搜索即可，欢迎大家来探店。
微扰酱18年毕业于上海交通大学，是一个在阿里、字节、腾讯都工作过的工程师，有丰富的面试经验。从 2021.4 开始在emqx从事存储研发，希望在今年多多输出。

最后，如果对你有帮助，可以点个赞支持一下我哦 也欢迎在leetcode上关注我。

统计信息

通过次数	提交次数	AC比率
2243	6818	32.9%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途