原文链接: https://leetcode-cn.com/problems/parallel-courses-iii

英文原文

You are given an integer n, which indicates that there are n courses labeled from 1 to n. You are also given a 2D integer array relations where relations[j] = [prevCoursej, nextCoursej] denotes that course prevCoursej has to be completed before course nextCoursej (prerequisite relationship). Furthermore, you are given a 0-indexed integer array time where time[i] denotes how many months it takes to complete the (i+1)th course.

You must find the minimum number of months needed to complete all the courses following these rules:

• You may start taking a course at any time if the prerequisites are met.
• Any number of courses can be taken at the same time.

Return the minimum number of months needed to complete all the courses.

Note: The test cases are generated such that it is possible to complete every course (i.e., the graph is a directed acyclic graph).

 

Example 1:

Input: n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
Output: 8
Explanation: The figure above represents the given graph and the time required to complete each course. 
We start course 1 and course 2 simultaneously at month 0.
Course 1 takes 3 months and course 2 takes 2 months to complete respectively.
Thus, the earliest time we can start course 3 is at month 3, and the total time required is 3 + 5 = 8 months.

Example 2:

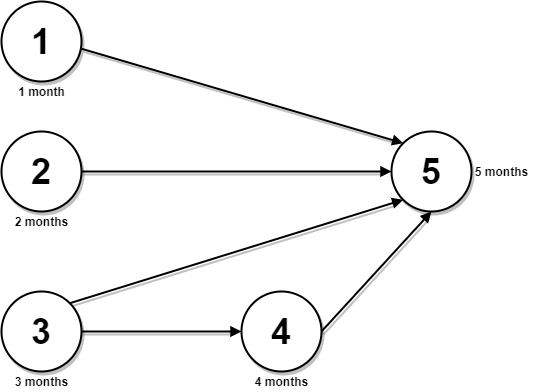
Input: n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
Output: 12
Explanation: The figure above represents the given graph and the time required to complete each course.
You can start courses 1, 2, and 3 at month 0.
You can complete them after 1, 2, and 3 months respectively.
Course 4 can be taken only after course 3 is completed, i.e., after 3 months. It is completed after 3 + 4 = 7 months.
Course 5 can be taken only after courses 1, 2, 3, and 4 have been completed, i.e., after max(1,2,3,7) = 7 months.
Thus, the minimum time needed to complete all the courses is 7 + 5 = 12 months.

 

Constraints:

• 1 <= n <= 5 * 104
• 0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)
• relations[j].length == 2
• 1 <= prevCoursej, nextCoursej <= n
• prevCoursej != nextCoursej
• All the pairs [prevCoursej, nextCoursej] are unique.
• time.length == n
• 1 <= time[i] <= 104
• The given graph is a directed acyclic graph.

中文题目

给你一个整数 n ，表示有 n 节课，课程编号从 1 到 n 。同时给你一个二维整数数组 relations ，其中 relations[j] = [prevCoursej, nextCoursej] ，表示课程 prevCoursej 必须在课程 nextCoursej 之前 完成（先修课的关系）。同时给你一个下标从 0 开始的整数数组 time ，其中 time[i] 表示完成第 (i+1) 门课程需要花费的 月份 数。

请你根据以下规则算出完成所有课程所需要的 最少 月份数：

• 如果一门课的所有先修课都已经完成，你可以在 任意 时间开始这门课程。
• 你可以 同时 上 任意门课程 。

请你返回完成所有课程所需要的 最少 月份数。

注意：测试数据保证一定可以完成所有课程（也就是先修课的关系构成一个有向无环图）。

 

示例 1:

输入：n = 3, relations = [[1,3],[2,3]], time = [3,2,5]
输出：8
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 和 2 。
课程 1 花费 3 个月，课程 2 花费 2 个月。
所以，最早开始课程 3 的时间是月份 3 ，完成所有课程所需时间为 3 + 5 = 8 个月。

示例 2：

输入：n = 5, relations = [[1,5],[2,5],[3,5],[3,4],[4,5]], time = [1,2,3,4,5]
输出：12
解释：上图展示了输入数据所表示的先修关系图，以及完成每门课程需要花费的时间。
你可以在月份 0 同时开始课程 1 ，2 和 3 。
在月份 1，2 和 3 分别完成这三门课程。
课程 4 需在课程 3 之后开始，也就是 3 个月后。课程 4 在 3 + 4 = 7 月完成。
课程 5 需在课程 1，2，3 和 4 之后开始，也就是在 max(1,2,3,7) = 7 月开始。
所以完成所有课程所需的最少时间为 7 + 5 = 12 个月。

 

提示：

• 1 <= n <= 5 * 104
• 0 <= relations.length <= min(n * (n - 1) / 2, 5 * 104)
• relations[j].length == 2
• 1 <= prevCoursej, nextCoursej <= n
• prevCoursej != nextCoursej
• 所有的先修课程对 [prevCoursej, nextCoursej] 都是 互不相同 的。
• time.length == n
• 1 <= time[i] <= 104
• 先修课程图是一个有向无环图。

通过代码

高赞题解

定义 $f[i]$ 表示完成第 $i$ 门课程需要花费的最少月份数。根据题意，只有当 $i$ 的所有先修课程都完成时，才可以开始 $i$，并且我们可以立即开始 $i$。

因此 $f[i]=\textit{time}[i] + \max f[j]$，这里 $j$ 是 $i$ 的所有先修课程。

由于题目保证图是一个有向无环图，所以一定存在拓扑排序。我们可以在求拓扑排序的同时，计算状态转移。

代码实现时，设当前节点为 $v$，我们可以在计算出 $f[v]$ 后，更新 $f[w]$ 的所有先修课程耗时的最大值，这里 $v$ 是 $w$ 的先修课程。

答案就是 $\max f[i]$。

相似题目：

• 1857. 有向图中最大颜色值

func minimumTime(n int, relations [][]int, time []int) (ans int) {
	g := make([][]int, n)
	deg := make([]int, n)
	for _, e := range relations {
		v, w := e[0]-1, e[1]-1
		g[v] = append(g[v], w)
		deg[w]++
	}

	q := make([]int, 0, n)
	for i, d := range deg {
		if d == 0 {
			q = append(q, i)
		}
	}
	f := make([]int, n)
	for len(q) > 0 {
		v := q[0]
		q = q[1:]
		f[v] += time[v] // 补上当前课程的时间
		ans = max(ans, f[v])
		for _, w := range g[v] {
			f[w] = max(f[w], f[v]) // 更新 f[w] 的所有先修课程耗时的最大值
			if deg[w]--; deg[w] == 0 {
				q = append(q, w)
			}
		}
	}
	return
}

func max(a, b int) int {
	if b > a {
		return b
	}
	return a
}

统计信息

通过次数	提交次数	AC比率
1955	3522	55.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言