原文链接: https://leetcode-cn.com/problems/number-of-valid-move-combinations-on-chessboard

英文原文

There is an 8 x 8 chessboard containing n pieces (rooks, queens, or bishops). You are given a string array pieces of length n, where pieces[i] describes the type (rook, queen, or bishop) of the ith piece. In addition, you are given a 2D integer array positions also of length n, where positions[i] = [ri, ci] indicates that the ith piece is currently at the 1-based coordinate (ri, ci) on the chessboard.

When making a move for a piece, you choose a destination square that the piece will travel toward and stop on.

• A rook can only travel horizontally or vertically from (r, c) to the direction of (r+1, c), (r-1, c), (r, c+1), or (r, c-1).
• A queen can only travel horizontally, vertically, or diagonally from (r, c) to the direction of (r+1, c), (r-1, c), (r, c+1), (r, c-1), (r+1, c+1), (r+1, c-1), (r-1, c+1), (r-1, c-1).
• A bishop can only travel diagonally from (r, c) to the direction of (r+1, c+1), (r+1, c-1), (r-1, c+1), (r-1, c-1).

You must make a move for every piece on the board simultaneously. A move combination consists of all the moves performed on all the given pieces. Every second, each piece will instantaneously travel one square towards their destination if they are not already at it. All pieces start traveling at the 0th second. A move combination is invalid if, at a given time, two or more pieces occupy the same square.

Return the number of valid move combinations​​​​​.

Notes:

• No two pieces will start in the same square.
• You may choose the square a piece is already on as its destination.
• If two pieces are directly adjacent to each other, it is valid for them to move past each other and swap positions in one second.

 

Example 1:

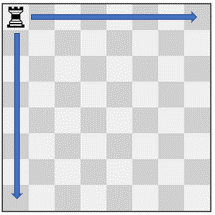
Input: pieces = ["rook"], positions = [[1,1]]
Output: 15
Explanation: The image above shows the possible squares the piece can move to.

Example 2:

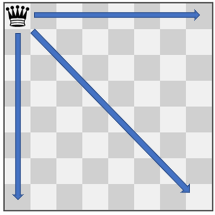
Input: pieces = ["queen"], positions = [[1,1]]
Output: 22
Explanation: The image above shows the possible squares the piece can move to.

Example 3:

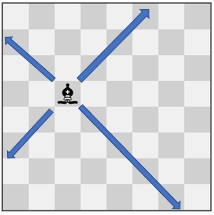
Input: pieces = ["bishop"], positions = [[4,3]]
Output: 12
Explanation: The image above shows the possible squares the piece can move to.

Example 4:

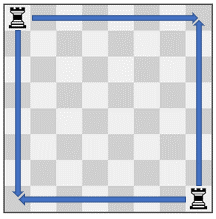
Input: pieces = ["rook","rook"], positions = [[1,1],[8,8]]
Output: 223
Explanation: There are 15 moves for each rook which results in 15 * 15 = 225 move combinations.
However, there are two invalid move combinations:
- Move both rooks to (8, 1), where they collide.
- Move both rooks to (1, 8), where they collide.
Thus there are 225 - 2 = 223 valid move combinations.
Note that there are two valid move combinations that would result in one rook at (1, 8) and the other at (8, 1).
Even though the board state is the same, these two move combinations are considered different since the moves themselves are different.

Example 5:

Input: pieces = ["queen","bishop"], positions = [[5,7],[3,4]]
Output: 281
Explanation: There are 12 * 24 = 288 move combinations.
However, there are several invalid move combinations:
- If the queen stops at (6, 7), it blocks the bishop from moving to (6, 7) or (7, 8).
- If the queen stops at (5, 6), it blocks the bishop from moving to (5, 6), (6, 7), or (7, 8).
- If the bishop stops at (5, 2), it blocks the queen from moving to (5, 2) or (5, 1).
Of the 288 move combinations, 281 are valid.

 

Constraints:

• n == pieces.length
• n == positions.length
• 1 <= n <= 4
• pieces only contains the strings "rook", "queen", and "bishop".
• There will be at most one queen on the chessboard.
• 1 <= xi, yi <= 8
• Each positions[i] is distinct.

中文题目

有一个 8 x 8 的棋盘，它包含 n 个棋子（棋子包括车，后和象三种）。给你一个长度为 n 的字符串数组 pieces ，其中 pieces[i] 表示第 i 个棋子的类型（车，后或象）。除此以外，还给你一个长度为 n 的二维整数数组 positions ，其中 positions[i] = [ri, ci] 表示第 i 个棋子现在在棋盘上的位置为 (ri, ci) ，棋盘下标从 1 开始。

棋盘上每个棋子都可以移动 至多一次 。每个棋子的移动中，首先选择移动的 方向 ，然后选择 移动的步数 ，同时你要确保移动过程中棋子不能移到棋盘以外的地方。棋子需按照以下规则移动：

• 车可以 水平或者竖直 从 (r, c) 沿着方向 (r+1, c)，(r-1, c)，(r, c+1) 或者 (r, c-1) 移动。
• 后可以 水平竖直或者斜对角 从 (r, c) 沿着方向 (r+1, c)，(r-1, c)，(r, c+1)，(r, c-1)，(r+1, c+1)，(r+1, c-1)，(r-1, c+1)，(r-1, c-1) 移动。
• 象可以 斜对角 从 (r, c) 沿着方向 (r+1, c+1)，(r+1, c-1)，(r-1, c+1)，(r-1, c-1) 移动。

移动组合 包含所有棋子的 移动 。每一秒，每个棋子都沿着它们选择的方向往前移动 一步 ，直到它们到达目标位置。所有棋子从时刻 0 开始移动。如果在某个时刻，两个或者更多棋子占据了同一个格子，那么这个移动组合 不有效 。

请你返回 有效 移动组合的数目。

注意：

• 初始时，不会有两个棋子 在 同一个位置 。
• 有可能在一个移动组合中，有棋子不移动。
• 如果两个棋子 直接相邻 且两个棋子下一秒要互相占据对方的位置，可以将它们在同一秒内 交换位置 。

 

示例 1:

输入：pieces = ["rook"], positions = [[1,1]]
输出：15
解释：上图展示了棋子所有可能的移动。

示例 2：

输入：pieces = ["queen"], positions = [[1,1]]
输出：22
解释：上图展示了棋子所有可能的移动。

示例 3:

输入：pieces = ["bishop"], positions = [[4,3]]
输出：12
解释：上图展示了棋子所有可能的移动。

示例 4:

输入：pieces = ["rook","rook"], positions = [[1,1],[8,8]]
输出：223
解释：每个车有 15 种移动，所以总共有 15 * 15 = 225 种移动组合。
但是，有两个是不有效的移动组合：
- 将两个车都移动到 (8, 1) ，会导致它们在同一个格子相遇。
- 将两个车都移动到 (1, 8) ，会导致它们在同一个格子相遇。
所以，总共有 225 - 2 = 223 种有效移动组合。
注意，有两种有效的移动组合，分别是一个车在 (1, 8) ，另一个车在 (8, 1) 。
即使棋盘状态是相同的，这两个移动组合被视为不同的，因为每个棋子移动操作是不相同的。

示例 5：

输入：pieces = ["queen","bishop"], positions = [[5,7],[3,4]]
输出：281
解释：总共有 12 * 24 = 288 种移动组合。
但是，有一些不有效的移动组合：
- 如果后停在 (6, 7) ，它会阻挡象到达 (6, 7) 或者 (7, 8) 。
- 如果后停在 (5, 6) ，它会阻挡象到达 (5, 6) ，(6, 7) 或者 (7, 8) 。
- 如果象停在 (5, 2) ，它会阻挡后到达 (5, 2) 或者 (5, 1) 。
在 288 个移动组合当中，281 个是有效的。

 

提示：

• n == pieces.length
• n == positions.length
• 1 <= n <= 4
• pieces 只包含字符串 "rook" ，"queen" 和 "bishop" 。
• 棋盘上总共最多只有一个后。
• 1 <= xi, yi <= 8
• 每一个 positions[i] 互不相同。

通过代码

高赞题解

预处理每个棋子的所有合法移动，然后递归判断，对当前递归的棋子的合法移动，判断是否与前面的棋子的合法移动相冲突，若无冲突则往下递归。

type move struct{ dx, dy, t int } // (dx,dy) 表示移动方向，t 表示移动的步数（时间）

func validMovesRook(x, y int) (m []move) {
	m = append(m, move{}) // 为了方便无重复地计算皇后
	for i := 1; i <= 8; i++ {
		if i != x {
			m = append(m, move{(i - x) / abs(i-x), 0, abs(i - x)})
		}
	}
	for j := 1; j <= 8; j++ {
		if j != y {
			m = append(m, move{0, (j - y) / abs(j-y), abs(j - y)})
		}
	}
	return
}

func validMovesBishop(x, y int) (m []move) {
	m = append(m, move{}) // 为了方便无重复地计算皇后
	for i := 1; i <= 8; i++ {
		for j := 1; j <= 8; j++ {
			if (i != x || j != y) && abs(i-x) == abs(j-y) {
				m = append(m, move{(i - x) / abs(i-x), (j - y) / abs(j-y), abs(i - x)})
			}
		}
	}
	return
}

func validMovesQueen(x, y int) []move { // 皇后可以有上面两种移动方式
	return append(append([]move{{}}, validMovesRook(x, y)[1:]...), validMovesBishop(x, y)[1:]...)
}

// 判断是否合法，即不存在两个棋子占据同一个格子的情况
func isValid(x1, y1, x2, y2 int, m1, m2 move) bool {
	for i := 1; i <= m1.t || i <= m2.t; i++ {
		if i <= m1.t {
			x1 += m1.dx // 每一秒走一步
			y1 += m1.dy
		}
		if i <= m2.t {
			x2 += m2.dx
			y2 += m2.dy
		}
		if x1 == x2 && y1 == y2 { // 两个棋子占据了同一个格子
			return false
		}
	}
	return true
}

func countCombinations(pieces []string, positions [][]int) (ans int) {
	n := len(pieces)
	validMoves := make([][]move, n)
	for i, p := range positions {
		x, y := p[0], p[1]
		if pieces[i] == "rook" {
			validMoves[i] = validMovesRook(x, y) // 预处理所有合法移动
		} else if pieces[i] == "bishop" {
			validMoves[i] = validMovesBishop(x, y)
		} else {
			validMoves[i] = validMovesQueen(x, y)
		}
	}

	moves := make([]move, n)
	var f func(int)
	f = func(i int) {
		if i == n {
			ans++
			return
		}
		x1, y1 := positions[i][0], positions[i][1]
	outer:
		for _, m := range validMoves[i] { // 枚举当前棋子的所有合法移动
			for j, pos := range positions[:i] { // 枚举前面的棋子的移动
				if !isValid(x1, y1, pos[0], pos[1], m, moves[j]) { // 判断该移动是否与前面的棋子的移动相冲突
					continue outer
				}
			}
			moves[i] = m // 无冲突
			f(i + 1) // 递归进入下一个棋子
		}
	}
	f(0)
	return
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

统计信息

通过次数	提交次数	AC比率
603	992	60.8%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言