2065-最大化一张图中的路径价值(Maximum Path Quality of a Graph)

原文链接: https://leetcode-cn.com/problems/maximum-path-quality-of-a-graph

英文原文

There is an undirected graph with n nodes numbered from 0 to n - 1 (inclusive). You are given a 0-indexed integer array values where values[i] is the value of the i^th node. You are also given a 0-indexed 2D integer array edges, where each edges[j] = [u_j, v_j, time_j] indicates that there is an undirected edge between the nodes u_j and v_j,and it takes time_j seconds to travel between the two nodes. Finally, you are given an integer maxTime.

A valid path in the graph is any path that starts at node 0, ends at node 0, and takes at most maxTime seconds to complete. You may visit the same node multiple times. The quality of a valid path is the sum of the values of the unique nodes visited in the path (each node's value is added at most once to the sum).

Return the maximum quality of a valid path.

Note: There are at most four edges connected to each node.

Example 1:

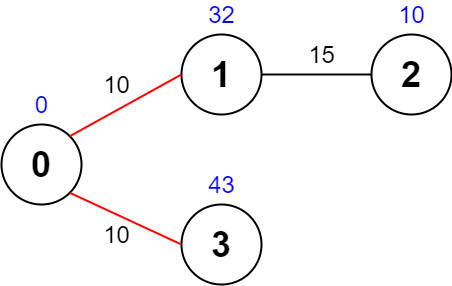
Input: values = [0,32,10,43], edges = [[0,1,10],[1,2,15],[0,3,10]], maxTime = 49
Output: 75
Explanation:
One possible path is 0 -> 1 -> 0 -> 3 -> 0. The total time taken is 10 + 10 + 10 + 10 = 40 <= 49.
The nodes visited are 0, 1, and 3, giving a maximal path quality of 0 + 32 + 43 = 75.

Example 2:

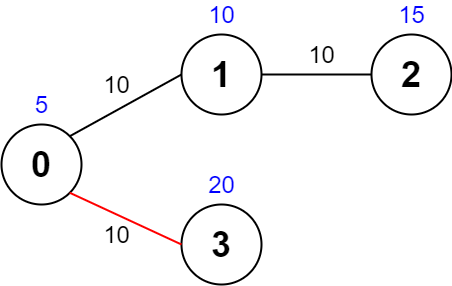
Input: values = [5,10,15,20], edges = [[0,1,10],[1,2,10],[0,3,10]], maxTime = 30
Output: 25
Explanation:
One possible path is 0 -> 3 -> 0. The total time taken is 10 + 10 = 20 <= 30.
The nodes visited are 0 and 3, giving a maximal path quality of 5 + 20 = 25.

Example 3:

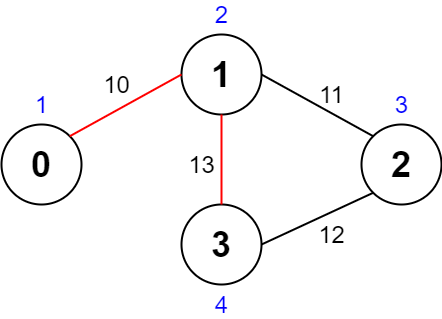
Input: values = [1,2,3,4], edges = [[0,1,10],[1,2,11],[2,3,12],[1,3,13]], maxTime = 50
Output: 7
Explanation:
One possible path is 0 -> 1 -> 3 -> 1 -> 0. The total time taken is 10 + 13 + 13 + 10 = 46 <= 50.
The nodes visited are 0, 1, and 3, giving a maximal path quality of 1 + 2 + 4 = 7.

Example 4:

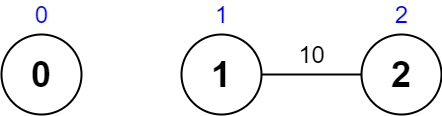
Input: values = [0,1,2], edges = [[1,2,10]], maxTime = 10
Output: 0
Explanation: 
The only path is 0. The total time taken is 0.
The only node visited is 0, giving a maximal path quality of 0.

Constraints:

n == values.length
1 <= n <= 1000
0 <= values[i] <= 10⁸
0 <= edges.length <= 2000
edges[j].length == 3
0 <= u_j< v_j <= n - 1
10 <= time_j, maxTime <= 100
All the pairs [u_j, v_j] are unique.
There are at most four edges connected to each node.
The graph may not be connected.

中文题目

给你一张无向图，图中有 n 个节点，节点编号从 0 到 n - 1 （都包括）。同时给你一个下标从 0 开始的整数数组 values ，其中 values[i] 是第 i 个节点的价值。同时给你一个下标从 0 开始的二维整数数组 edges ，其中 edges[j] = [u_j, v_j, time_j] 表示节点 u_j 和 v_j 之间有一条需要 time_j 秒才能通过的无向边。最后，给你一个整数 maxTime 。

合法路径 指的是图中任意一条从节点 0 开始，最终回到节点 0 ，且花费的总时间 不超过 maxTime 秒的一条路径。你可以访问一个节点任意次。一条合法路径的价值定义为路径中 不同节点 的价值之和（每个节点的价值至多算入价值总和中一次）。

请你返回一条合法路径的最大价值。

注意：每个节点至多有四条边与之相连。

示例 1：

输入：values = [0,32,10,43], edges = [[0,1,10],[1,2,15],[0,3,10]], maxTime = 49
输出：75
解释：
一条可能的路径为：0 -> 1 -> 0 -> 3 -> 0 。总花费时间为 10 + 10 + 10 + 10 = 40 <= 49 。
访问过的节点为 0 ，1 和 3 ，最大路径价值为 0 + 32 + 43 = 75 。

示例 2：

输入：values = [5,10,15,20], edges = [[0,1,10],[1,2,10],[0,3,10]], maxTime = 30
输出：25
解释：
一条可能的路径为：0 -> 3 -> 0 。总花费时间为 10 + 10 = 20 <= 30 。
访问过的节点为 0 和 3 ，最大路径价值为 5 + 20 = 25 。

示例 3：

输入：values = [1,2,3,4], edges = [[0,1,10],[1,2,11],[2,3,12],[1,3,13]], maxTime = 50
输出：7
解释：
一条可能的路径为：0 -> 1 -> 3 -> 1 -> 0 。总花费时间为 10 + 13 + 13 + 10 = 46 <= 50 。
访问过的节点为 0 ，1 和 3 ，最大路径价值为 1 + 2 + 4 = 7 。

示例 4：

输入：values = [0,1,2], edges = [[1,2,10]], maxTime = 10
输出：0
解释：
唯一一条路径为 0 。总花费时间为 0 。
唯一访问过的节点为 0 ，最大路径价值为 0 。

提示：

n == values.length
1 <= n <= 1000
0 <= values[i] <= 10⁸
0 <= edges.length <= 2000
edges[j].length == 3
0 <= u_j< v_j <= n - 1
10 <= time_j, maxTime <= 100
[u_j, v_j] 所有节点对 互不相同 。
每个节点 至多有四条 边。
图可能不连通。

通过代码

高赞题解

根据题目的数据范围，至多能走 $10$ 条边，这意味着搜索的层数至多为 $10$；同时，题目保证每个节点至多有四条边与之相连，因此每次搜索时至多会递归 $4$ 次。因此计算量至多为 $4^{10}$，可以在时限内跑完。

本题的一个剪枝技巧是，先预处理起点 $0$ 到其余节点的最短路，在搜索时提前判断下一个节点在走最短路的前提下能否在 $\textit{maxTime}$ 时间内回到起点 $0$，若不能则不进行递归。

func maximalPathQuality(values []int, edges [][]int, maxTime int) (ans int) {
	n := len(values)
	g := make([][]edge, n)
	for _, e := range edges {
		v, w, t := e[0], e[1], e[2]
		g[v] = append(g[v], edge{w, t}) // 建图
		g[w] = append(g[w], edge{v, t})
	}

	dis := dijkstra(g, 0) // 预处理从起点 0 到每个点的最短路

	vis := make([]bool, n)
	sum := 0
	var dfs func(int, int)
	dfs = func(v, time int) {
		if !vis[v] { // 没有访问时，更新价值之和
			vis[v] = true
			sum += values[v]
			if sum > ans {
				ans = sum // 更新答案
			}
			defer func() {
				sum -= values[v] // 恢复现场
				vis[v] = false
			}()
		}
		for _, e := range g[v] {
			if time+e.t+dis[e.to] <= maxTime { // 剪枝：下个节点在走最短路的情况下可以在 maxTime 时间内返回起点 0
				dfs(e.to, time+e.t)
			}
		}
	}
	dfs(0, 0)
	return
}

// 下面是求最短路的模板
type edge struct{ to, t int }
type pair struct{ v, dis int }
type hp []pair

func (h hp) Len() int              { return len(h) }
func (h hp) Less(i, j int) bool    { return h[i].dis < h[j].dis }
func (h hp) Swap(i, j int)         { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v interface{})   { *h = append(*h, v.(pair)) }
func (h *hp) Pop() (v interface{}) { a := *h; *h, v = a[:len(a)-1], a[len(a)-1]; return }
func (h *hp) push(v pair)          { heap.Push(h, v) }
func (h *hp) pop() pair            { return heap.Pop(h).(pair) }

func dijkstra(g [][]edge, start int) []int {
	dis := make([]int, len(g))
	for i := range dis {
		dis[i] = 1e9
	}
	dis[start] = 0
	h := hp{{start, 0}}
	for len(h) > 0 {
		vd := h.pop()
		v := vd.v
		if dis[v] < vd.dis {
			continue
		}
		for _, e := range g[v] {
			w, wt := e.to, e.t
			if newD := dis[v] + wt; newD < dis[w] {
				dis[w] = newD
				h.push(pair{w, dis[w]})
			}
		}
	}
	return dis
}

统计信息

通过次数	提交次数	AC比率
1895	3536	53.6%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途