原文链接: https://leetcode-cn.com/problems/count-fertile-pyramids-in-a-land

英文原文

A farmer has a rectangular grid of land with m rows and n columns that can be divided into unit cells. Each cell is either fertile (represented by a 1) or barren (represented by a 0). All cells outside the grid are considered barren.

A pyramidal plot of land can be defined as a set of cells with the following criteria:

1. The number of cells in the set has to be greater than 1 and all cells must be fertile.
2. The apex of a pyramid is the topmost cell of the pyramid. The height of a pyramid is the number of rows it covers. Let (r, c) be the apex of the pyramid, and its height be h. Then, the plot comprises of cells (i, j) where r <= i <= r + h - 1 and c - (i - r) <= j <= c + (i - r).

An inverse pyramidal plot of land can be defined as a set of cells with similar criteria:

1. The number of cells in the set has to be greater than 1 and all cells must be fertile.
2. The apex of an inverse pyramid is the bottommost cell of the inverse pyramid. The height of an inverse pyramid is the number of rows it covers. Let (r, c) be the apex of the pyramid, and its height be h. Then, the plot comprises of cells (i, j) where r - h + 1 <= i <= r and c - (r - i) <= j <= c + (r - i).

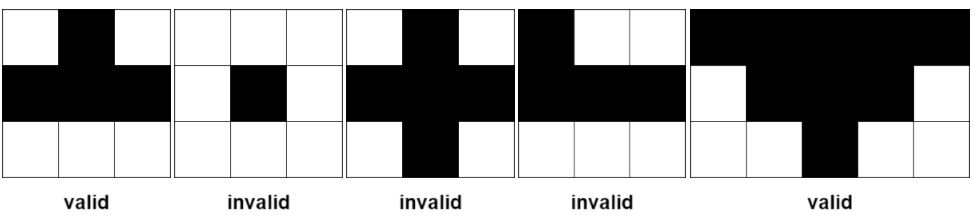
Some examples of valid and invalid pyramidal (and inverse pyramidal) plots are shown below. Black cells indicate fertile cells.

Given a 0-indexed m x n binary matrix grid representing the farmland, return the total number of pyramidal and inverse pyramidal plots that can be found in grid.

 

Example 1:

  

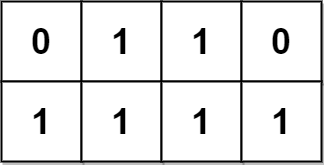
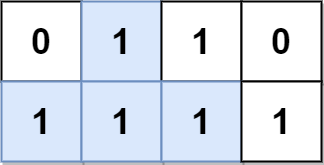
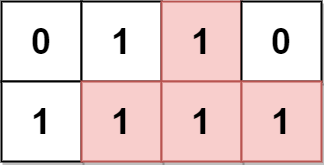
Input: grid = [[0,1,1,0],[1,1,1,1]]
Output: 2
Explanation:
The 2 possible pyramidal plots are shown in blue and red respectively.
There are no inverse pyramidal plots in this grid. 
Hence total number of pyramidal and inverse pyramidal plots is 2 + 0 = 2.

Example 2:

  

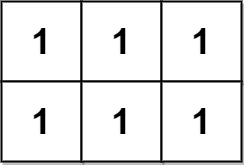
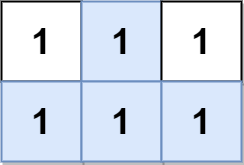
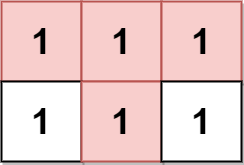
Input: grid = [[1,1,1],[1,1,1]]
Output: 2
Explanation:
The pyramidal plot is shown in blue, and the inverse pyramidal plot is shown in red. 
Hence the total number of plots is 1 + 1 = 2.

Example 3:

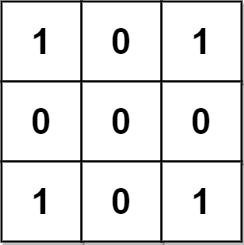
Input: grid = [[1,0,1],[0,0,0],[1,0,1]]
Output: 0
Explanation:
There are no pyramidal or inverse pyramidal plots in the grid.

Example 4:

   

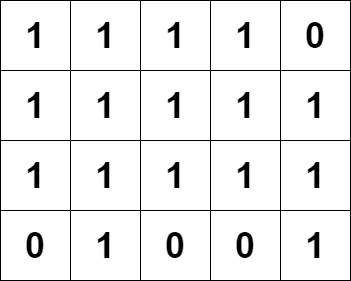
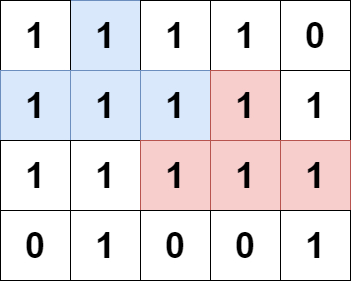
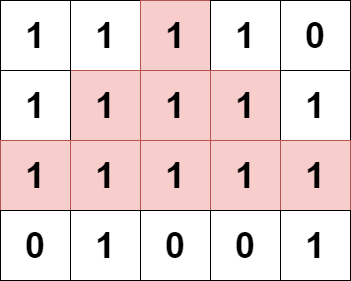
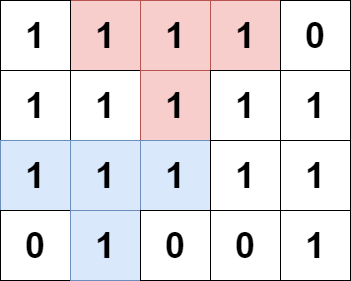
Input: grid = [[1,1,1,1,0],[1,1,1,1,1],[1,1,1,1,1],[0,1,0,0,1]]
Output: 13
Explanation:
There are 7 pyramidal plots, 3 of which are shown in the 2nd and 3rd figures.
There are 6 inverse pyramidal plots, 2 of which are shown in the last figure.
The total number of plots is 7 + 6 = 13.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 1000
• 1 <= m * n <= 105
• grid[i][j] is either 0 or 1.

中文题目

有一个 矩形网格 状的农场，划分为 m 行 n 列的单元格。每个格子要么是 肥沃的 （用 1 表示），要么是 贫瘠 的（用 0 表示）。网格图以外的所有与格子都视为贫瘠的。

农场中的 金字塔 区域定义如下：

1. 区域内格子数目 大于 1 且所有格子都是 肥沃的 。
2. 金字塔 顶端 是这个金字塔 最上方 的格子。金字塔的高度是它所覆盖的行数。令 (r, c) 为金字塔的顶端且高度为 h ，那么金字塔区域内包含的任一格子 (i, j) 需满足 r <= i <= r + h - 1 且 c - (i - r) <= j <= c + (i - r) 。

一个 倒金字塔 类似定义如下：

1. 区域内格子数目 大于 1 且所有格子都是 肥沃的 。
2. 倒金字塔的 顶端 是这个倒金字塔 最下方 的格子。倒金字塔的高度是它所覆盖的行数。令 (r, c) 为金字塔的顶端且高度为 h ，那么金字塔区域内包含的任一格子 (i, j) 需满足 r - h + 1 <= i <= r 且 c - (r - i) <= j <= c + (r - i) 。

下图展示了部分符合定义和不符合定义的金字塔区域。黑色区域表示肥沃的格子。

给你一个下标从 0 开始且大小为 m x n 的二进制矩阵 grid ，它表示农场，请你返回 grid 中金字塔和倒金字塔的 总数目 。

 

示例 1：

  

输入：grid = [[0,1,1,0],[1,1,1,1]]
输出：2
解释：
2 个可能的金字塔区域分别如上图蓝色和红色区域所示。
这个网格图中没有倒金字塔区域。
所以金字塔区域总数为 2 + 0 = 2 。

示例 2：

  

输入：grid = [[1,1,1],[1,1,1]]
输出：2
解释：
金字塔区域如上图蓝色区域所示，倒金字塔如上图红色区域所示。
所以金字塔区域总数目为 1 + 1 = 2 。

示例 3：

输入：grid = [[1,0,1],[0,0,0],[1,0,1]]
输出：0
解释：
网格图中没有任何金字塔或倒金字塔区域。

示例 4：

   

输入：grid = [[1,1,1,1,0],[1,1,1,1,1],[1,1,1,1,1],[0,1,0,0,1]]
输出：13
解释：
有 7 个金字塔区域。上图第二和第三张图中展示了它们中的 3 个。
有 6 个倒金字塔区域。上图中最后一张图展示了它们中的 2 个。
所以金字塔区域总数目为 7 + 6 = 13.

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 1000
• 1 <= m * n <= 105
• grid[i][j] 要么是 0 ，要么是 1 。

通过代码

高赞题解

先求正金字塔。

定义 $\textit{dp}[i][j]$ 表示金字塔顶端位于 $(i,j)$ 时的最大层数（$1$ 层也算）。如果顶端在 $(i,j)$ 的金字塔最大能有 $x$ 层，那么顶端在 $(i,j)$ 的金字塔也可以有 $x-1,x-2,\cdots,1$ 层。由于要求区域内格子数目大于 $1$，统计答案的时候把 $1$ 层去掉，因此有 $x-1$ 个以 $(i,j)$ 为顶端的金字塔。

我们从 $\textit{grid}$ 的最后一行开始往上递推。转移的策略是在 $(i+1,j)$ 处的最大金字塔上套一层倒 V 型的「外壳」。具体来说，从 $(i,j)$ 出发向左下方向前进，求出能达到的最长连续 $1$ 的个数，根据 $\textit{dp}$ 的定义，这就是 $\textit{dp}[i+1][j-1]+1$；同理，向右下方向前进，能达到的最长连续 $1$ 的个数为 $\textit{dp}[i+1][j+1]+1$。取左右最长连续 $1$ 的个数的最小值即为「外壳」的高度。那么 $(i,j)$ 处的最大金字塔的高度为「外壳」的高度与 $(i+1,j)$ 处最大金字塔高度 $+1$ 的最小值。

即

$$
\textit{dp}[i][j] = \min(\min(\textit{dp}[i+1][j-1]+1, \textit{dp}[i+1][j+1]+1), \textit{dp}[i+1][j]+1)
$$

倒金字塔可以将 $\textit{grid}$ 上下颠倒后再求一遍正金字塔即可。

相似题目：

• CF1393D - Rarity and New Dress

func countPyramids(grid [][]int) (ans int) {
	m, n := len(grid), len(grid[0])
	dp := make([][]int, m)
	for i := range dp {
		dp[i] = make([]int, n)
	}

	f := func() {
		dp[m-1] = grid[m-1]
		for i := m - 2; i >= 0; i-- {
			dp[i][0] = grid[i][0]
			dp[i][n-1] = grid[i][n-1]
			for j := 1; j < n-1; j++ {
				if grid[i][j] == 0 {
					dp[i][j] = 0
				} else {
					dp[i][j] = min(min(dp[i+1][j-1], dp[i+1][j+1]), dp[i+1][j]) + 1
					ans += dp[i][j] - 1
				}
			}
		}
	}
	f() // 求正金字塔个数
	for i := 0; i < m/2; i++ { // 上下颠倒
		grid[i], grid[m-1-i] = grid[m-1-i], grid[i]
	}
	f() // 再求一遍正金字塔个数
	return
}

func min(a, b int) int { if a > b {return b}; return a }

统计信息

通过次数	提交次数	AC比率
1310	2176	60.2%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言