212-单词搜索 II(Word Search II)

原文链接: https://leetcode-cn.com/problems/word-search-ii

英文原文

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:

Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Example 2:

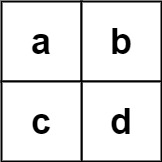
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []

Constraints:

m == board.length
n == board[i].length
1 <= m, n <= 12
board[i][j] is a lowercase English letter.
1 <= words.length <= 3 * 10⁴
1 <= words[i].length <= 10
words[i] consists of lowercase English letters.
All the strings of words are unique.

中文题目

给定一个 m x n 二维字符网格 board 和一个单词（字符串）列表 words，找出所有同时在二维网格和字典中出现的单词。

单词必须按照字母顺序，通过 相邻的单元格 内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母在一个单词中不允许被重复使用。

示例 1：

输入：board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
输出：["eat","oath"]

示例 2：

输入：board = [["a","b"],["c","d"]], words = ["abcb"]
输出：[]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 12
board[i][j] 是一个小写英文字母
1 <= words.length <= 3 * 10⁴
1 <= words[i].length <= 10
words[i] 由小写英文字母组成
words 中的所有字符串互不相同

通过代码

高赞题解

回溯算法

数据范围只有 $12$，且 words 中出现的单词长度不会超过 $10$，可以考虑使用「回溯算法」。

起始先将所有 words 出现的单词放到 Set 结构中，然后以 board 中的每个点作为起点进行爆搜（由于题目规定在一个单词中每个格子只能被使用一次，因此还需要一个 vis 数组来记录访问过的位置）：

如果当前爆搜到的字符串长度超过 $10$，直接剪枝；
如果当前搜索到的字符串在 Set 中，则添加到答案（同时了防止下一次再搜索到该字符串，需要将该字符串从 Set 中移除）。

代码：

[]
class Solution {
    Set<String> set = new HashSet<>();
    List<String> ans = new ArrayList<>();
    char[][] board;
    int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
    int n, m;
    boolean[][] vis = new boolean[15][15];
    public List<String> findWords(char[][] _board, String[] words) {
        board = _board;
        m = board.length; n = board[0].length;
        for (String w : words) set.add(w);
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                vis[i][j] = true;
                sb.append(board[i][j]);
                dfs(i, j, sb);
                vis[i][j] = false;
                sb.deleteCharAt(sb.length() - 1);
            }
        }
        return ans;
    }
    void dfs(int i, int j, StringBuilder sb) {
        if (sb.length() > 10) return ;
        if (set.contains(sb.toString())) {
            ans.add(sb.toString());
            set.remove(sb.toString());
        }
        for (int[] d : dirs) {
            int dx = i + d[0], dy = j + d[1];
            if (dx < 0 || dx >= m || dy < 0 || dy >= n) continue;
            if (vis[dx][dy]) continue;
            vis[dx][dy] = true;
            sb.append(board[dx][dy]);
            dfs(dx, dy, sb);
            vis[dx][dy] = false;
            sb.deleteCharAt(sb.length() - 1);
        }
    }
}

时间复杂度：共有 $m * n$ 个起点，每次能往 $4$ 个方向搜索（不考虑重复搜索问题），且搜索的长度不会超过 $10$。整体复杂度为 $O(m * n * 4^{10})$
空间复杂度：$O(\sum_{i=0}^{words.length - 1} words[i].length)$

Trie

在「解法一」中，对于任意一个当前位置 $(i, j)$，我们都不可避免的搜索了四联通的全部方向，这导致了那些无效搜索路径最终只有长度达到 $10$ 才会被剪枝。

要进一步优化我们的搜索过程，需要考虑如何在每一步的搜索中进行剪枝。

我们可以使用 $Trie$ 结构进行建树，对于任意一个当前位置 $(i, j)$ 而言，只有在 $Trie$ 中存在往从字符 $a$ 到 $b$ 的边时，我们才在棋盘上搜索从 $a$ 到 $b$ 的相邻路径。

不了解 $Trie$ 的同学，可以看看这里，里面写了两种实现 $Trie$ 的方式。

对于本题，我们可以使用「TrieNode」的方式进行建 $Trie$。

因为 words 里最多有 $10^4$ 个单词，每个单词长度最多为 $10$，如果开成静态数组的话，不考虑共用行的问题，我们需要开一个大小为 $10^5 * 26$ 的大数组，可能会有 TLE 或 MLE 的风险。

与此同时，我们需要将平时建 $TrieNode$ 中的 isEnd 标记属性直接换成记录当前字符 s，这样我们在 DFS 的过程中则无须额外记录当前搜索字符串。

代码：

[]
class Solution {
    class TrieNode {
        String s;
        TrieNode[] tns = new TrieNode[26];
    }
    void insert(String s) {
        TrieNode p = root;
        for (int i = 0; i < s.length(); i++) {
            int u = s.charAt(i) - 'a';
            if (p.tns[u] == null) p.tns[u] = new TrieNode();
            p = p.tns[u];
        }
        p.s = s;
    }
    Set<String> set = new HashSet<>();
    char[][] board;
    int n, m;
    TrieNode root = new TrieNode();
    int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
    boolean[][] vis = new boolean[15][15];
    public List<String> findWords(char[][] _board, String[] words) {
        board = _board;
        m = board.length; n = board[0].length;
        for (String w : words) insert(w);
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                int u = board[i][j] - 'a';
                if (root.tns[u] != null) {
                    vis[i][j] = true;
                    dfs(i, j, root.tns[u]);
                    vis[i][j] = false;
                }
            }
        }
        List<String> ans = new ArrayList<>();
        for (String s : set) ans.add(s);
        return ans;
    }
    void dfs(int i, int j, TrieNode node) {
        if (node.s != null) set.add(node.s);
        for (int[] d : dirs) {
            int dx = i + d[0], dy = j + d[1];
            if (dx < 0 || dx >= m || dy < 0 || dy >= n) continue;
            if (vis[dx][dy]) continue;
            int u = board[dx][dy] - 'a';
            if (node.tns[u] != null) {
                vis[dx][dy] = true;
                dfs(dx, dy, node.tns[u]);
                vis[dx][dy] = false;
            }
        }
    }
}

时间复杂度：共有 $m * n$ 个起点，每次能往 $4$ 个方向搜索（不考虑重复搜索问题），且搜索的长度不会超过 $10$。整体复杂度为 $O(m * n * 4^{10})$
空间复杂度：$O(\sum_{i=0}^{words.length - 1} words[i].length * C)$，$C$ 为字符集大小，固定为 $26$

最后

如果有帮助到你，请给题解点个赞和收藏，让更多的人看到 ~ (“▔□▔)/

也欢迎你关注我（公主号后台回复「送书」即可参与长期看题解学算法送实体书活动）或加入「组队打卡」小群，提供写「证明」&「思路」的高质量题解。

所有题解已经加入刷题指南，欢迎 star 哦 ~

统计信息

通过次数	提交次数	AC比率
65521	140860	46.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
单词搜索	中等
不同路径 III	困难

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途