363-矩形区域不超过 K 的最大数值和(Max Sum of Rectangle No Larger Than K)

原文链接: https://leetcode-cn.com/problems/max-sum-of-rectangle-no-larger-than-k

英文原文

Given an m x n matrix matrix and an integer k, return the max sum of a rectangle in the matrix such that its sum is no larger than k.

It is guaranteed that there will be a rectangle with a sum no larger than k.

Example 1:

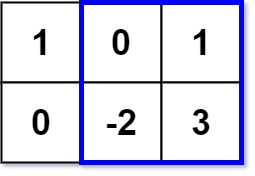
Input: matrix = [[1,0,1],[0,-2,3]], k = 2
Output: 2
Explanation: Because the sum of the blue rectangle [[0, 1], [-2, 3]] is 2, and 2 is the max number no larger than k (k = 2).

Example 2:

Input: matrix = [[2,2,-1]], k = 3
Output: 3

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-100 <= matrix[i][j] <= 100
-10⁵ <= k <= 10⁵

Follow up: What if the number of rows is much larger than the number of columns?

中文题目

给你一个 m x n 的矩阵 matrix 和一个整数 k ，找出并返回矩阵内部矩形区域的不超过 k 的最大数值和。

题目数据保证总会存在一个数值和不超过 k 的矩形区域。

示例 1：

输入：matrix = [[1,0,1],[0,-2,3]], k = 2
输出：2
解释：蓝色边框圈出来的矩形区域 [[0, 1], [-2, 3]] 的数值和是 2，且 2 是不超过 k 的最大数字（k = 2）。

示例 2：

输入：matrix = [[2,2,-1]], k = 3
输出：3

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-100 <= matrix[i][j] <= 100
-10⁵ <= k <= 10⁵

进阶：如果行数远大于列数，该如何设计解决方案？

通过代码

高赞题解

一、暴力 + 动态规划

枚举矩形的左上角、右下角，从 (i1, j1) 到 (i2, j2)
从左上角、到右下角的矩形区域数值和：黄色 = 绿色 + 橙色 - 蓝色 + (i2, j2)

<, , , >

状态转移方程为 dp(i1,j1,i2,j2) = dp(i1,j1,i2 - 1,j2) + dp(i1,j1,i2,j2 - 1) - dp(i1,j1,i2 - 1,j2 - 1) + matrix[i2 - 1][j2 - 1];
四层遍历，时间复杂度 $O(m^2n^2)$，空间复杂度 $O(m^2n^2)$
超出内存限制
- 思路有戏，进一步压缩状态试试

public int maxSumSubmatrix(int[][] matrix, int k) {
    int rows = matrix.length, cols = matrix[0].length, max = Integer.MIN_VALUE;
    int[][][][] dp = new int[rows + 1][cols + 1][rows + 1][cols + 1]; // from (i1,j1) to (i2,j2)
    for (int i1 = 1; i1 <= rows; i1++) {
        for (int j1 = 1; j1 <= cols; j1++) {
            dp[i1][j1][i1][j1] = matrix[i1 - 1][j1 - 1];
            for (int i2 = i1; i2 <= rows; i2++) {
                for (int j2 = j1; j2 <= cols; j2++) {
                    dp[i1][j1][i2][j2] = dp[i1][j1][i2 - 1][j2] + dp[i1][j1][i2][j2 - 1] - dp[i1][j1][i2 - 1][j2 - 1] + matrix[i2 - 1][j2 - 1];
                    if (dp[i1][j1][i2][j2] <= k && dp[i1][j1][i2][j2] > max) max = dp[i1][j1][i2][j2];
                }
            }
        }
    }
    return max;
}

二、暴力 + 动态规划 + 状态压缩

从上述代码发现，每次更换左上角 (i, j) 之后，之前记录的值都没用过了
尝试每次更换左上角时就重复利用 dp，故只需记录右下角即可
依然四层遍历，时间复杂度 $O(m^2n^2)$，空间复杂度 $O(mn)$

public int maxSumSubmatrix(int[][] matrix, int k) {
    int rows = matrix.length, cols = matrix[0].length, max = Integer.MIN_VALUE;
    for (int i1 = 1; i1 <= rows; i1++) {
        for (int j1 = 1; j1 <= cols; j1++) {
            int[][] dp = new int[rows + 1][cols + 1]; // renew  // from (i1,j1) to (i2,j2)
            dp[i1][j1] = matrix[i1 - 1][j1 - 1];
            for (int i2 = i1; i2 <= rows; i2++) {
                for (int j2 = j1; j2 <= cols; j2++) {
                    dp[i2][j2] = dp[i2 - 1][j2] + dp[i2][j2 - 1] - dp[i2 - 1][j2 - 1] + matrix[i2 - 1][j2 - 1];
                    if (dp[i2][j2] <= k && dp[i2][j2] > max) max = dp[i2][j2];
                }
            }
        }
    }
    return max;
}

三、数组滚动

看过大神的思路 @powcai 固定左右边界，前缀和+二分
- 固定左右边界 ……这句一下就把思路打开了
- 虽然看不懂 python..但还是不能放弃呀

先固定左右边界，不断压入行累计数组

public int maxSumSubmatrix(int[][] matrix, int k) {
    int rows = matrix.length, cols = matrix[0].length, max = Integer.MIN_VALUE;
    // O(cols ^ 2 * rows)
    for (int l = 0; l < cols; l++) { // 枚举左边界
        int[] rowSum = new int[rows]; // 左边界改变才算区域的重新开始
        for (int r = l; r < cols; r++) { // 枚举右边界
            for (int i = 0; i < rows; i++) { // 按每一行累计到 dp
                rowSum[i] += matrix[i][r];
            }

            // ？？？
        }
    }
    return max;
}

画图感受一下

左边界从 0 开始
右边界从左边界开始（即同一列）
rowSum 数组，记录两个边界中间的 每一行 的和

表演开始了
右边界 r 向右移动
rowSum 数组，记录两个边界中间的 每一行 的和
- 累加新来的

这张过后你也豁然开朗了吗
右边界 r 继续向右移动
rowSum 数组，仍然记录两个边界中间的 每一行 的和
- 继续累加新来的即可

rowSum 有何用

以 l、r 为左右界的，任意矩形的面积，即 rowSum 连续子数组的和

再让我们回到代码

public int maxSumSubmatrix(int[][] matrix, int k) {
    int rows = matrix.length, cols = matrix[0].length, max = Integer.MIN_VALUE;
    // O(cols ^ 2 * rows)
    for (int l = 0; l < cols; l++) { // 枚举左边界
        int[] rowSum = new int[rows]; // 左边界改变才算区域的重新开始
        for (int r = l; r < cols; r++) { // 枚举右边界
            for (int i = 0; i < rows; i++) { // 按每一行累计到 dp
                rowSum[i] += matrix[i][r];
            }

            // 求 rowSum 连续子数组 的 和
            // 和 尽量大，但不大于 k
            max = Math.max(max, dpmax(rowSum, k));
        }
    }
    return max;
}

// 在数组 arr 中，求不超过 k 的最大值
private int dpmax(int[] arr, int k) {
    // TODO
}

问题进入到最后一个环节，完善 dpmax()

暴力求最大值

枚举子数组起点、终点，累计中间元素
此时的运行时间已经起飞很多了

// 在数组 arr 中，求不超过 k 的最大值
private int dpmax(int[] arr, int k) {
    // O(rows ^ 2)
    int max = Integer.MIN_VALUE;
    for (int l = 0; l < arr.length; l++) {
        int sum = 0;
        for (int r = l; r < arr.length; r++) {
            sum += arr[r];
            if (sum > max && sum <= k) max = sum;
        }
    }
    return max;
}

可是我们就是要完美一下呢

并不是所有时候都值得遍历找 k

先来这题：53. 最大子序和，有一种解法是

public int maxSubArray(int[] nums) {
    int len = nums.length, max, dp;
    if (len == 0) return 0;
    // 要尽量大，就尽量不要负数
    dp = max = nums[0];
    for (int i = 1; i < len; i++) {
        if (dp > 0) dp += nums[i]; // 之前的和 > 0，那就累计进来
        else dp = nums[i]; // 之前的和 <= 0，那就重新开始
        if (dp > max) max = dp; // max = Math.max(max, dp);
    }
    return max;
}

先画图感受一下

开始遍历数组 [4, 3, -1, -7, -9, 6, 2, -7]

此时出现了 之前的和小于0 的情况
那下一个数开始，咱就不要之前的了，另起炉灶（还是连续两次另立炉灶）

最终得到 [6, 2] 这个区间的子数组和最大，最大值 8
这里复杂的是还要 不大于 k 怎么办？

继续深入细究 k

假设 k = Integer.MAX_VALUE ，那么上述数组不小于 k 的最大子数组和为 8
假设 k = 100 ，那么上述数组不小于 k 的最大子数组和仍然为 8
你也许注意到了，要是 k 很大，大过上述滚动玩法的最大值，那结果就是上述的 8
那如果 k == 8 呢？太棒了，就是 8 咯，最好的最大值
那如果 k < 8 呢，假设 k = 5
回顾我们 dp 一路滚过来的值 [4, 7, 6, -1, -9, 6, 8, 1]
- 难道不大于 k = 5 的子数组的最大值就是 4 吗？是的，这里看起来是
- 注意这是 dp 一路滚来的值，不是数组原值
  - 原数组是 [4, 3, -1, -7, -9, 6, 2, -7]
如果我们再在原数组后增加 14 形成 [4, 3, -1, -7, -9, 6, 2, -7, 14]
则结果应该是 整个数组 的和 5，而不是 因为前面的 -9 而断开累计
怎么办？——暴力就好了（在下只能暴力了…还有别的法子吗…）

[]
// 隔壁有完整代码
// 在数组 arr 中，求不超过 k 的最大值
private int dpmax(int[] arr, int k) {
    int rollSum = arr[0], rollMax = rollSum;
    // O(rows)
    for (int i = 1; i < arr.length; i++) {
        if (rollSum > 0) rollSum += arr[i];
        else rollSum = arr[i];
        if (rollSum > rollMax) rollMax = rollSum;
    }
    if (rollMax <= k) return rollMax;
    // O(rows ^ 2)
    int max = Integer.MIN_VALUE;
    for (int l = 0; l < arr.length; l++) {
        int sum = 0;
        for (int r = l; r < arr.length; r++) {
            sum += arr[r];
            if (sum > max && sum <= k) max = sum;
            if (max == k) return k; // 尽量提前
        }
    }
    return max;
}

[]
// 附上完整代码
public int maxSumSubmatrix(int[][] matrix, int k) {
    int rows = matrix.length, cols = matrix[0].length, max = Integer.MIN_VALUE;
    // O(cols ^ 2 * rows)
    for (int l = 0; l < cols; l++) { // 枚举左边界
        int[] rowSum = new int[rows]; // 左边界改变才算区域的重新开始
        for (int r = l; r < cols; r++) { // 枚举右边界
            for (int i = 0; i < rows; i++) { // 按每一行累计到 dp
                rowSum[i] += matrix[i][r];
            }
            max = Math.max(max, dpmax(rowSum, k));
            if (max == k) return k; // 尽量提前
        }
    }
    return max;
}
// 在数组 arr 中，求不超过 k 的最大值
private int dpmax(int[] arr, int k) {
    int rollSum = arr[0], rollMax = rollSum;
    // O(rows)
    for (int i = 1; i < arr.length; i++) {
        if (rollSum > 0) rollSum += arr[i];
        else rollSum = arr[i];
        if (rollSum > rollMax) rollMax = rollSum;
    }
    if (rollMax <= k) return rollMax;
    // O(rows ^ 2)
    int max = Integer.MIN_VALUE;
    for (int l = 0; l < arr.length; l++) {
        int sum = 0;
        for (int r = l; r < arr.length; r++) {
            sum += arr[r];
            if (sum > max && sum <= k) max = sum;
            if (max == k) return k; // 尽量提前
        }
    }
    return max;
}

得，愉快的大半天又没了，可是你能看到这儿，笔者还是很开心，值了：）

统计信息

通过次数	提交次数	AC比率
33688	68968	48.8%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途

英文原文

中文题目

通过代码

高赞题解

一、暴力 + 动态规划

二、暴力 + 动态规划 + 状态压缩

三、数组滚动

先固定左右边界，不断压入行累计数组

画图感受一下

rowSum 有何用

暴力求最大值

并不是所有时候都值得遍历找 k

先画图感受一下

继续深入细究 k

统计信息

提交历史

你的赏识是我前进的动力

英文原文

中文题目

通过代码

高赞题解

一、暴力 + 动态规划

二、暴力 + 动态规划 + 状态压缩

三、数组滚动

先固定左右边界，不断压入 行累计数组

画图感受一下

rowSum 有何用

暴力求最大值

并不是所有时候都值得遍历找 k

先画图感受一下

继续深入细究 k

统计信息

提交历史

你的赏识是我前进的动力

先固定左右边界，不断压入行累计数组