391-完美矩形(Perfect Rectangle)

原文链接: https://leetcode-cn.com/problems/perfect-rectangle

英文原文

Given an array rectangles where rectangles[i] = [x_i, y_i, a_i, b_i] represents an axis-aligned rectangle. The bottom-left point of the rectangle is (x_i, y_i) and the top-right point of it is (a_i, b_i).

Return true if all the rectangles together form an exact cover of a rectangular region.

Example 1:

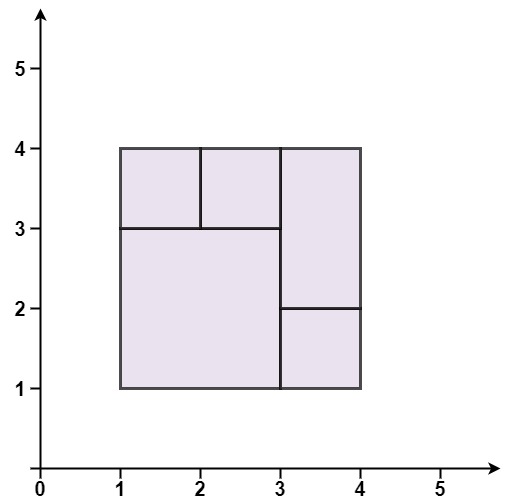
Input: rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
Output: true
Explanation: All 5 rectangles together form an exact cover of a rectangular region.

Example 2:

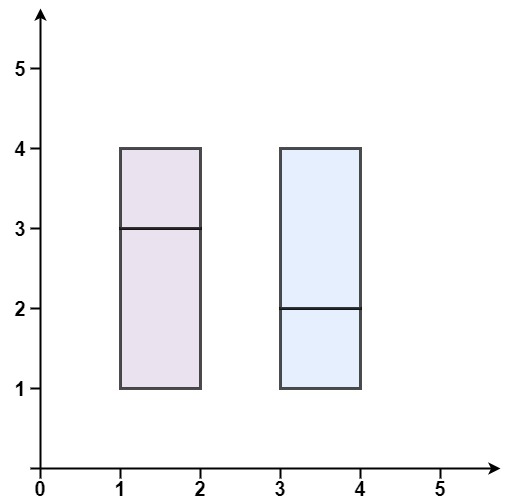
Input: rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
Output: false
Explanation: Because there is a gap between the two rectangular regions.

Example 3:

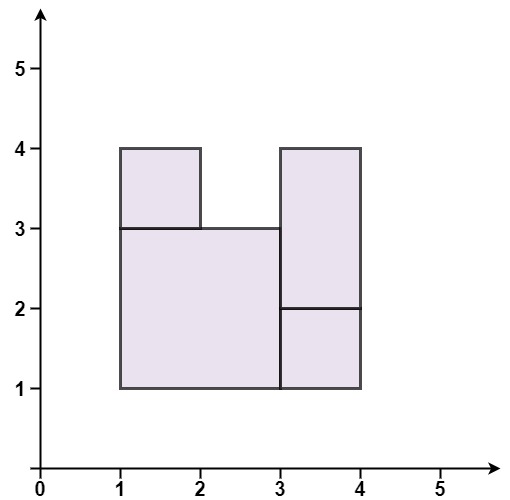
Input: rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[3,2,4,4]]
Output: false
Explanation: Because there is a gap in the top center.

Example 4:

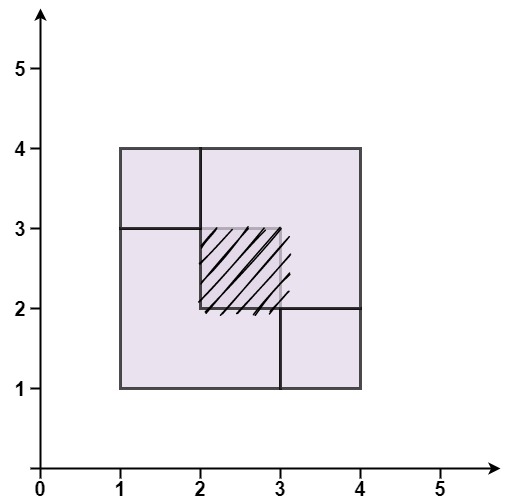
Input: rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
Output: false
Explanation: Because two of the rectangles overlap with each other.

Constraints:

1 <= rectangles.length <= 2 * 10⁴
rectangles[i].length == 4
-10⁵ <= x_i, y_i, a_i, b_i <= 10⁵

中文题目

给你一个数组 rectangles ，其中 rectangles[i] = [x_i, y_i, a_i, b_i] 表示一个坐标轴平行的矩形。这个矩形的左下顶点是 (x_i, y_i) ，右上顶点是 (a_i, b_i) 。

如果所有矩形一起精确覆盖了某个矩形区域，则返回 true ；否则，返回 false 。

示例 1：

输入：rectangles = [[1,1,3,3],[3,1,4,2],[3,2,4,4],[1,3,2,4],[2,3,3,4]]
输出：true
解释：5 个矩形一起可以精确地覆盖一个矩形区域。

示例 2：

输入：rectangles = [[1,1,2,3],[1,3,2,4],[3,1,4,2],[3,2,4,4]]
输出：false
解释：两个矩形之间有间隔，无法覆盖成一个矩形。

示例 3：

输入：rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[3,2,4,4]]
输出：false
解释：图形顶端留有空缺，无法覆盖成一个矩形。

示例 4：

输入：rectangles = [[1,1,3,3],[3,1,4,2],[1,3,2,4],[2,2,4,4]]
输出：false
解释：因为中间有相交区域，虽然形成了矩形，但不是精确覆盖。

提示：

1 <= rectangles.length <= 2 * 10⁴
rectangles[i].length == 4
-10⁵ <= x_i, y_i, a_i, b_i <= 10⁵

通过代码

高赞题解

扫描线

将每个矩形 $rectangles[i]$ 看做两条竖直方向的边，使用 $(x, y1, y2)$ 的形式进行存储（其中 $y1$ 代表该竖边的下端点，$y2$ 代表竖边的上端点），同时为了区分是矩形的左边还是右边，再引入一个标识位，即以四元组 $(x, y1, y2, flag)$ 的形式进行存储。

一个完美矩形的充要条件为：对于完美矩形的每一条非边缘的竖边，都「成对」出现（存在两条完全相同的左边和右边重叠在一起）；对于完美矩形的两条边缘竖边，均独立为一条连续的（不重叠）的竖边。

如图（红色框的为「完美矩形的边缘竖边」，绿框的为「完美矩形的非边缘竖边」）：

绿色：非边缘竖边必然有成对的左右两条完全相同的竖边重叠在一起；
红色：边缘竖边由于只有单边，必然不重叠，且连接成一条完成的竖边。

代码（感谢 @ricecake 同学提供的 Python3 代码）：

[]
class Solution {
    public boolean isRectangleCover(int[][] rectangles) {
        int n = rectangles.length;
        int[][] rs = new int[n * 2][4];
        for (int i = 0, idx = 0; i < n; i++) {
            int[] re = rectangles[i];
            rs[idx++] = new int[]{re[0], re[1], re[3], 1};
            rs[idx++] = new int[]{re[2], re[1], re[3], -1};
        }
        Arrays.sort(rs, (a,b)->{
            if (a[0] != b[0]) return a[0] - b[0];
            return a[1] - b[1];
        });
        n *= 2;
        // 分别存储相同的横坐标下「左边的线段」和「右边的线段」 (y1, y2)
        List<int[]> l1 = new ArrayList<>(), l2 = new ArrayList<>(); 
        for (int l = 0; l < n; ) {
            int r = l;
            l1.clear(); l2.clear();
            // 找到横坐标相同部分
            while (r < n && rs[r][0] == rs[l][0]) r++;
            for (int i = l; i < r; i++) {
                int[] cur = new int[]{rs[i][1], rs[i][2]};
                List<int[]> list = rs[i][3] == 1 ? l1 : l2;
                if (list.isEmpty()) {
                    list.add(cur);
                } else {
                    int[] prev = list.get(list.size() - 1);
                    if (cur[0] < prev[1]) return false; // 存在重叠
                    else if (cur[0] == prev[1]) prev[1] = cur[1]; // 首尾相连
                    else list.add(cur); 
                }
            }
            if (l > 0 && r < n) {
                // 若不是完美矩形的边缘竖边，检查是否成对出现
                if (l1.size() != l2.size()) return false;
                for (int i = 0; i < l1.size(); i++) {
                    if (l1.get(i)[0] == l2.get(i)[0] && l1.get(i)[1] == l2.get(i)[1]) continue;
                    return false;
                }
            } else {
                // 若是完美矩形的边缘竖边，检查是否形成完整一段
                if (l1.size() + l2.size() != 1) return false;
            }
            l = r;
        }
        return true;
    }
}

[]
class Solution:
    def isRectangleCover(self, rectangles: List[List[int]]) -> bool:
        if not rectangles:
            return False
        n = len(rectangles)
        # 解析数据，(x, y, a, b) -> (x, y, b, 1) ，(a, y, b, -1)
        # 最后一位表示是矩形的左边缘还是右边缘（即扫描线的“上升”和“下降”）
        rs = []
        for rec in rectangles:
            x, y, a, b = rec
            rs.append([x, y, b, 1])
            rs.append([a, y, b, -1])
        rs.sort()
        
        l = r = 0
        while r < len(rs):
            l1 = [] # 记录“上升”的线段
            l2 = [] # 记录“下降”的线段
            while r < len(rs) and rs[r][0] == rs[l][0]:
                r += 1
            for i in range(l, r): # 遍历横坐标相同的线段
                x, y1, y2, isUp = rs[i]
                curl = l1 if isUp == 1 else l2 
                if not curl:
                    curl.append([y1, y2])
                else:
                    if curl[-1][1] > y1: # 有重叠
                        return False 
                    elif curl[-1][1] == y1: # 能连接上，进行连接
                        curl[-1][1] = y2 
                    else: # 不能连接上，记录新的一段
                        curl.append([y1, y2])
            # 若处理的是最左边的边或最右边的边，此时应连成一个线段
            if l == 0 or r == len(rs): 
                if len(l1) + len(l2) != 1:
                    return False 
            else:
                # 若处理的是中间的扫描线，此时上升的线段和下降的线段应完全相同才能正好重叠
                if len(l1) != len(l2):
                    return False 
                for i in range(len(l1)):
                    if l1[i] != l2[i]:
                        return False 
            l = r # 进入下一个横坐标的扫描
        return True

时间复杂度：将 rectangles 划分成边集的复杂度为 $O(n)$；对边集进行排序的复杂度为 $O(n\log{n})$，对排序好的边集进行遍历检查，每条边会被扫描线性次，复杂度为 $O(n)$。整体复杂度为 $O(n\log{n})$
空间复杂度：$O(n)$

其他「扫描线」问题

考虑加练如下「扫描线」问题 🍭🍭🍭

题目	题解	难度	推荐指数
218. 天际线问题	LeetCode 题解链接	困难	🤩🤩🤩
391. 完美矩形	LeetCode 题解链接	困难	🤩🤩🤩🤩

注：以上目录整理来自 wiki，任何形式的转载引用请保留出处。

最后

如果有帮助到你，请给题解点个赞和收藏，让更多的人看到 ~ (“▔□▔)/

也欢迎你关注我（公主号后台回复「送书」即可参与长期看题解学算法送实体书活动）或加入「组队打卡」小群，提供写「证明」&「思路」的高质量题解。

所有题解已经加入刷题指南，欢迎 star 哦 ~

统计信息

通过次数	提交次数	AC比率
21395	45626	46.9%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途