原文链接: https://leetcode-cn.com/problems/trapping-rain-water-ii

英文原文

Given an m x n integer matrix heightMap representing the height of each unit cell in a 2D elevation map, return the volume of water it can trap after raining.

 

Example 1:

Input: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
Output: 4
Explanation: After the rain, water is trapped between the blocks.
We have two small ponds 1 and 3 units trapped.
The total volume of water trapped is 4.

Example 2:

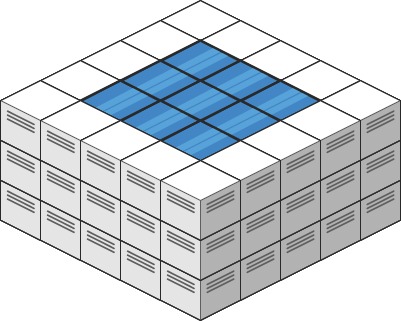
Input: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
Output: 10

 

Constraints:

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 <= heightMap[i][j] <= 2 * 104

中文题目

给你一个 m x n 的矩阵，其中的值均为非负整数，代表二维高度图每个单元的高度，请计算图中形状最多能接多少体积的雨水。

 

示例 1:

输入: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
输出: 4
解释: 下雨后，雨水将会被上图蓝色的方块中。总的接雨水量为1+2+1=4。

示例 2:

输入: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
输出: 10

 

提示:

• m == heightMap.length
• n == heightMap[i].length
• 1 <= m, n <= 200
• 0 <= heightMap[i][j] <= 2 * 104

 

通过代码

高赞题解

解题思路

前言：可能不是最好的思路，如果有好的思路麻烦大佬们艾特我学习下！谢谢了！

接雨水I中，我们维护了左右两个最高的墙，那么在这里，就是维护周围一个圈，用堆来维护周围这一圈中的最小元素。为什么是维护最小的元素不是最大的元素呢，因为木桶原理呀。这个最小的元素从堆里弹出来，和它四个方向的元素去比较大小，看能不能往里灌水，怎么灌水呢，如果用方向就比较复杂了，我们可以用visited数组来表示哪些遍历过，哪些没遍历过。如果当前弹出来的高度比它周围的大，他就能往矮的里面灌水了，灌水后要把下一个柱子放进去的时候，放的高度要取两者较大的，也就是灌水后的高度，不是它原来矮的时候的高度了，如果不能灌水，继续走。

Given the following 3x6 height map:
[
  [1,4,3,1,3,2],
  [3,2,1,3,2,4],
  [2,3,3,2,3,1]
]

就拿这个例子来说，我们先把第一圈都放进去，然后开始从堆中弹出，第一圈，最小值是1（遍历时候标记为访问过），1从堆里弹出来，比如弹出来1(坐标[0,3])，它下方的3没有被访问过，尝试灌水，发现不能灌水，3入堆，然后继续弹。比如说，我此时弹出来一个3（坐标[1,0]），它能向右边2(坐标[1,1])灌水，那这边就可以统计了，然后我们要插入2(坐标[1,1])这个位置，但是插入的时候，要记得你得是插入的高度得是灌水后的高度，而不是原来的高度了

当然我这边只是举个例子哈

代码

class Solution {
    public int trapRainWater(int[][] heights) {
        if (heights == null || heights.length == 0) return 0;
        int n = heights.length;
        int m = heights[0].length;
        // 用一个vis数组来标记这个位置有没有被访问过
        boolean[][] vis = new boolean[n][m];
        // 优先队列中存放三元组 [x,y,h] 坐标和高度
        PriorityQueue<int[]> pq = new PriorityQueue<>((o1, o2) -> o1[2] - o2[2]);

        // 先把最外一圈放进去
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (i == 0 || i == n - 1 || j == 0 || j == m - 1) {
                    pq.offer(new int[]{i, j, heights[i][j]});
                    vis[i][j] = true;
                }
            }
        }
        int res = 0;
        // 方向数组，把dx和dy压缩成一维来做
        int[] dirs = {-1, 0, 1, 0, -1};
        while (!pq.isEmpty()) {
            int[] poll = pq.poll();
            // 看一下周围四个方向，没访问过的话能不能往里灌水
            for (int k = 0; k < 4; k++) {
                int nx = poll[0] + dirs[k];
                int ny = poll[1] + dirs[k + 1];
                // 如果位置合法且没访问过
                if (nx >= 0 && nx < n && ny >= 0 && ny < m && !vis[nx][ny]) {
                    // 如果外围这一圈中最小的比当前这个还高，那就说明能往里面灌水啊
                    if (poll[2] > heights[nx][ny]) {
                        res += poll[2] - heights[nx][ny];
                    }
                    // 如果灌水高度得是你灌水后的高度了，如果没灌水也要取高的
                    pq.offer(new int[]{nx, ny, Math.max(heights[nx][ny], poll[2])});
                    vis[nx][ny] = true;
                }
            }
        }
        return res;
    }
}

统计信息

通过次数	提交次数	AC比率
25014	43169	57.9%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
接雨水	困难