原文链接: https://leetcode-cn.com/problems/freedom-trail

英文原文

In the video game Fallout 4, the quest "Road to Freedom" requires players to reach a metal dial called the "Freedom Trail Ring" and use the dial to spell a specific keyword to open the door.

Given a string ring that represents the code engraved on the outer ring and another string key that represents the keyword that needs to be spelled, return the minimum number of steps to spell all the characters in the keyword.

Initially, the first character of the ring is aligned at the "12:00" direction. You should spell all the characters in key one by one by rotating ring clockwise or anticlockwise to make each character of the string key aligned at the "12:00" direction and then by pressing the center button.

At the stage of rotating the ring to spell the key character key[i]:

1. You can rotate the ring clockwise or anticlockwise by one place, which counts as one step. The final purpose of the rotation is to align one of ring's characters at the "12:00" direction, where this character must equal key[i].
2. If the character key[i] has been aligned at the "12:00" direction, press the center button to spell, which also counts as one step. After the pressing, you could begin to spell the next character in the key (next stage). Otherwise, you have finished all the spelling.

 

Example 1:

Input: ring = "godding", key = "gd"
Output: 4
Explanation:
For the first key character 'g', since it is already in place, we just need 1 step to spell this character. 
For the second key character 'd', we need to rotate the ring "godding" anticlockwise by two steps to make it become "ddinggo".
Also, we need 1 more step for spelling.
So the final output is 4.

Example 2:

Input: ring = "godding", key = "godding"
Output: 13

 

Constraints:

• 1 <= ring.length, key.length <= 100
• ring and key consist of only lower case English letters.
• It is guaranteed that key could always be spelled by rotating ring.

中文题目

电子游戏“辐射4”中，任务“通向自由”要求玩家到达名为“Freedom Trail Ring”的金属表盘，并使用表盘拼写特定关键词才能开门。

给定一个字符串 ring，表示刻在外环上的编码；给定另一个字符串 key，表示需要拼写的关键词。您需要算出能够拼写关键词中所有字符的最少步数。

最初，ring 的第一个字符与12:00方向对齐。您需要顺时针或逆时针旋转 ring 以使 key 的一个字符在 12:00 方向对齐，然后按下中心按钮，以此逐个拼写完 key 中的所有字符。

旋转 ring 拼出 key 字符 key[i] 的阶段中：

1. 您可以将 ring 顺时针或逆时针旋转一个位置，计为1步。旋转的最终目的是将字符串 ring 的一个字符与 12:00 方向对齐，并且这个字符必须等于字符 key[i] 。
2. 如果字符 key[i] 已经对齐到12:00方向，您需要按下中心按钮进行拼写，这也将算作 1 步。按完之后，您可以开始拼写 key 的下一个字符（下一阶段）, 直至完成所有拼写。

示例：

 

 

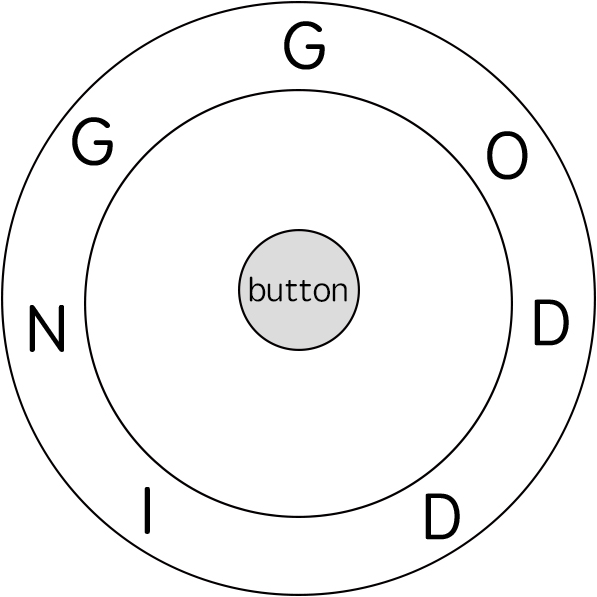
输入: ring = "godding", key = "gd"
输出: 4
解释:
 对于 key 的第一个字符 'g'，已经在正确的位置, 我们只需要1步来拼写这个字符。 
 对于 key 的第二个字符 'd'，我们需要逆时针旋转 ring "godding" 2步使它变成 "ddinggo"。
 当然, 我们还需要1步进行拼写。
 因此最终的输出是 4。

提示：

1. ring 和 key 的字符串长度取值范围均为 1 至 100；
2. 两个字符串中都只有小写字符，并且均可能存在重复字符；
3. 字符串 key 一定可以由字符串 ring 旋转拼出。

通过代码

高赞题解

解题思路

按惯例，先赞后看，日薪百万！

这题刚一拿到，哼，这么简单。然后我就陷入了死循环。

while 1:
    print(解答错误)
    print(超时)

这个题太复杂了，而且在我写这篇题解的时候，没有看到一个非常浅显易懂的面向我们这种菜鸡的由浅入深的题解。
于是，把我失败的过程和思路改良的变化都写出来，供大家参考。
顺带说一句，我的所有题解大部分都是 Python 写的，因为 Python 写的比较清晰简单，更类似伪代码。
写的时候我尽量都不使用一些 Python 特殊的自带库或者方法(如果用到的话我会尽量将清楚原理和其他语言的实现方法)，所以基本上这些方法都可以稍微调整一下，适用于其他的语言。

每个人的喜好不同关注点也不一样啦，大佬们闲太啰嗦的话可以直接跳到最后面看代码哈。

---

第一节 循环

先看题目，这个题首先我们要解决的是一个转盘电话拨号的问题。
看着是左转右转，题目描述里也是左转右转的。
其实并不用转。我们可以保持 ring 字符串不动，找到一个箭头 start 指向初始的字母，然后再拿一个箭头 target 指向目标的字母。

把这个转动改成双指针的问题：找到在字符串 ring 上，从 start 到 target 的最短移动距离。

这里，如果移动到了字符串的头，再往前一个，就等于指向了字符串的尾巴，同理，字符串的尾巴再往后一个就等于指向字符串的头。
这样就相当于字符转围成了一个环。我们要找到这个最短移动距离。
大家看这段代码。

Test 是字符串， target 就是我们要找的字母。
我们首先设计一个起始点 i ，比如说设为 0。
然后两个指针，一个 left 不断往左移动，一个 right 不断往右移动。
两个计数器，一个 lc ，一个 rc 都是用来计数的，表示指针移动了几次。
剩下的就很简答了，当左指针没有指到目标字母的时候就一直往左移动，移动到头了就把它瞬移到字符串末尾，继续往左移动。
右指针也是同理。
最后我们就可以找到左指针的移动次数和右指针的移动次数，来判断哪个方向的移动距离更短。

[]
Test = "godding"
target = "d"

i = 0

left = i
lc = 0
right = i
rc = 0

while Test[left] != target:
    left -= 1
    lc += 1
    if left == -1:
        left = len(Test) - 1

while Test[right] != target:
    right += 1
    rc += 1
    if right == len(Test):
        right = 0


print(left, lc)
print(right, rc)

当然，这个方法效率并不高，不过原理明白了对于我们下面一步一步讲解有好处的。请各位大佬不要喷我，我们一点一点往后讲。

---

第二节 小试身手（为什么贪心不行）

好了，既然搞明白了循环是怎么玩的，那下一步我们就可以直接上手做题了。
我们把上面的代码稍作改动，封装为一个函数，很容易写出下面的代码。

[]
class Solution:
    def findRotateSteps(self, ring: str, key: str) -> int:

        def FindX(target, current):
            i = current

            left = i
            lc = 0
            right = i
            rc = 0

            while ring[left] != target:
                left -= 1
                lc += 1
                if left == -1:
                    left = len(ring) - 1

            while ring[right] != target:
                right += 1
                rc += 1
                if right == len(ring):
                    right = 0
            
            if lc <= rc:
                return lc, left
            else:
                return rc, right

        start = 0
        counter = 0
        for target in key:
            move, new = FindX(target, start)
            counter = counter + move + 1
            start = new

        return counter

很激动很开心！测试！
然后就仿佛 当头一棒晴天霹雳泪水流下下载缓慢
解答错误！

我们来看一下是什么例子错误了。
ring："iotfo"
key： "fioot"

其实我们这段代码，就是类似于贪心算法。
贪心算法是什么，一句话简单概括下来就是：解决问题的每一步，都要取这一步的最优解。
换句话说，每一步它都不能吃亏，必须当下立马拿到最优解。

比如我们这个题，上面的代码每一步都是比较从左去找和从右去找的较短值。然后选择它，再往下一步。
但是这么做有一个问题，如果 从左去找 和 从右去找 是一样的，怎么办。
比如刚才这个例子，当我们找到 i 下一步要找 o 的时候，我们发现有两个 o ，到左边的 o 和到右边的 o 是一样的。

我这段代码是默认相等时取了左边，但是这个题里明显取 i = 1 的 o 是对于后面找 t 来说更佳。
所以我们就遇到了问题。同时也证明了贪心算法是不合理的。

有读者可能会说，那你改成右边不就行了，但是可能会遇到左边最佳的情况。并且，这个题里还有可能这一步牺牲一下，换取后面一步的胜利这种情况。所以贪心是不可行的。

---

第三节 分情况考虑

第一节和第二节我们搞明白了怎么找最短移动距离，以及贪心算法不行。
我们可以发现一个规律，其实对于每次找字母，都有两种情况。

1. 去左边找
2. 去右边找

那么其实，如果我们把所有情况都分析到了，其实不就能找到最佳选择了么。
没错，那我们就把这个方法写出来看一下。

下面的代码也比较容易看懂，相当于每一步，我们都同时考虑了向左走和向右走两种情况。
并且我们把所有情况最后的距离都记录下来，然后取一个最小值就是最后答案。

[]
class Solution:
    def findRotateSteps(self, ring: str, key: str) -> int:

        def FindX(target, current):
            i = current

            left = i
            lc = 0
            right = i
            rc = 0

            while ring[left] != target:
                left -= 1
                lc += 1
                if left == -1:
                    left = len(ring) - 1

            while ring[right] != target:
                right += 1
                rc += 1
                if right == len(ring):
                    right = 0
            
            # print("Left", lc, left)
            # print("Right", rc, right)

            return lc, left, rc, right

        counter = []
        Path = d()

        def BestSearch(start, target, c):

            if target == len(key):
                counter.append(c)
                return

            lc, left, rc, right = FindX(key[target], start)
            BestSearch(left, target + 1, c + lc + 1)  # 走左边
            BestSearch(right, target + 1, c + rc + 1) # 走右边


        BestSearch(0, 0, 0)

        return min(counter)

这么做固然没错，但是就像二叉树一样。虽然只有 100 个字符长度，但是情况分支最下端就相当于有 2的100次方 那么多个情况。
这对于电脑的计算能力和内存来说，就像核弹一样。
所以这段代码提交以后结果固然是超时。

---

第四节 改进求距离方法

为了提升时间效率，我们需要大幅改进代码。

首先，我们要改进一下找最短距离的方法。大家看下面这段代码。

d1 = abs(target - start)
d2 = abs(len(ring) - d1)
newc = min(d1, d2)

这段代码其实就能算出来从左或者从右的最短距离，比我们刚才的两轮 while 循环要快得多。
它的原理是什么呢，就是先做一个减法取绝对值， d1 其实就是 start 和 target 在字符串上的 **正向的差** 。比如 b = 1 f = 5 string = [abcdefg] 他们的差就是 b -> cdef d1 = 4。
但是因为字符串可以循环，d2 就是求如果不是正向的，那就相当于求反向的距离，其实就是字符串剩下的长度了。比如 b = 1 f = 5 string = [abcdefg] b -> agf d2 = 3。
我们只需要取较小的一个值，就是最短移动距离了。

---

第五节 改进二叉树结构

其实我们这么去考虑，在第二节里，我们的代码之所以会出错，其实就是因为有 **重复的** 字母。

我们这么想，对于 key 里的任何一个字母比如 x ，我们可以使用 ring 里的任何一个位置的 x 去匹配。

这句话非常重要。

所以我们并不需要每一步都考虑 去左边 和 去右边，这两种情况。
而是：遇到了 key 里的一个字母比如 x，当 ring 里有好几个 x 的时候，我们要分情况，考虑到底要用哪个 x 。

这样一来，我们的思维整体结构就变了。

我们要去把每一个 key 里字母可以用哪些位置的 ring 里字母先找到出来。
如下代码。
这里使用了一个 defaultdict，对于喜欢深究的朋友补充说一下，不喜欢的朋友直接无视即可不影响做题。其实它就是一个默认的空字典，所有值默认位0，并且可以自己扩张容量。直接调用不会出现 keyError，更好用一点。对于 C 的用户来说避免 keyError 可能更容易，直接建立一个空数组，然后memset全部初始化即可。Java 用户可以选用 Arrays.fill。

这样，我们就建立了一个 Choices 字典，
字典里的键，代表了一个目标 key 里的字母。
字典里键的值，是一个列表，代表了一个目标 key 里的字母，可以选择哪些位置的 ring 里字母去用。

from collections import defaultdict as d

Choices = d()  # 把每个key对应的可选的ring的字母的index做成字典。
for k in key:
    if k in Choices:
        continue
    else:
        Choices[k] = []
        for ri, r in enumerate(ring):
            if r == k:
                Choices[k].append(ri)

至此，我们的所有准备工作都已经完成了。
准备决战。

---

第六节 最终战役

根据我们第五节讨论的内容。其实这个题目变成了，

对于 key 里的任何一个字母比如 x ，我们去查找 ring 里的所有可能的 x 去匹配。并计算距离，找到最小的距离，进行距离累计。就是到达这个 x 的最小花费。
我们需要查看 key 里的最后一个字母，所对应的几种情况的花费并且找出来最小的那个数就可以了。

什么意思呢，再看一下这个图就好理解了。

我们已经查到了每个位置的 key 的字母的可以选择的 ring 上的位置。我们做一个稍微复杂的结构把他们列出来，如图。
首先每一个大括号，都代表一个 key 的字母的几种情况。比如对于

ring = “abcabcb” key = “ab”

a 的选择有两个，位置分别位 0 和 3
b 的选择有三个，位置分别位 1, 4 和 6

然后每个数字后面的值，就是目前的累计距离。

总结一下就是，每一个 key 的字母对应一个字典元素。
每一个字典元素里的每一个键，代表使用了 ring 上的这个位置的字母，然后后面的值，表示当前的距离累计。

所以最开始，我们可以写出来整个结构，但是距离累计都是 0，我们下面要开始算这些值。

初始我们放一个 {0:0} 的值。代表起点从 0 号位置开始的距离是 0。

首先，因为起点只有一个，所以对于 key 的第一个字母 a，它可以使用 ring 上的第 0 号位置的字母 或者 使用 ring 上的第 3 号位置的字母。
我们需要使用刚才优化后的循环方法去计算，从 起点 0 到 0 号位置 和 从 起点 0 到 3 号位置的距离。并且赋值给两个元素。

（图里的距离都是最后加了1的距离）

注意，这种方法不需要跳过 key 的首字母。也不需要对 key 的首字母和 ring 的首字母相同时做什么特殊处理。

在这个过程中，我们再建立一个 Path 字典，用来保存所有的相关情况，避免重复查找。

Path = d()

previous_distance = counter[keyi][start] # 先不用深究这个，就知道它是代表上一个元素的距离的就行。

s = str(start) + "-" + str(choice)  # 避免出现 start=1 choice = 10 和 start=11 choice = 0变成同样的键的情况。
if s not in Path:  # 不在Path里的话就加进去。
    d1 = abs(choice - start)
    d2 = abs(len(ring) - d1)
    newc = min(d1, d2)
    Path[s] = newc

temp.append(previous_distance + Path[s])  # 这里还没有加1，可以先不要管。

好了，目前我们知道了，找到 key 的第一个字母 a，有两种方法，分别是用 ring 上的第 0 号位置的字母 或者 使用 ring 上的第 3 号位置的字母。
他们的花费距离也都列在表里了。
下面我们再去看 key 的第二个字母 b。

我们刚才已经找到了 a ，所以新的起点，就是刚才的终点，也就是分别为 0 和 3。
所以问题变成 6 个分支，
对于使用 1 号位置的b来说，有两种方法可以到达它，一种是上一步用了 0 号位置的 a ，另一种是上一步用了 3 号位置的 a 。
我们分别计算两条路线的距离，
上一步用了 0 号位置的 a -> 这一步使用1号位置的b： 总花费是 1 + 2 = 3
上一步用了 3 号位置的 a -> 这一步使用1号位置的b： 总花费是 4 + 3 = 7
那么明显如果第二次要用 1 号位置的b的话，刚才那一步用了 0 号位置的 a 比较划算，所以我们就保留 3 。

同理。
对于使用 4 号位置的b来说，有两种方法可以到达它，一种是上一步用了 0 号位置的 a ，另一种是上一步用了 3 号位置的 a
对于使用 6 号位置的 b 来说，有两种方法可以到达它，一种是上一步用了 0 号位置的 a ，另一种是上一步用了 3 号位置的 a

计算下来，我们填好表格。

然后我们发现，最后选择使用 1 号位置的 b 和选择使用 6 号位置的 b 的总距离都是 3。
所以答案就是 3 了。

详细的信息可以看下面的代码。
至于这个方法的归类，可以说是深度优先搜索？可以说是动态规划？
反正不管怎么样我们把它做出来了。

PS：其实还可以再优化一些，比如我们没必要保留所有的格子，只需要保留前一个就行了。
但是没必要改了，就这样吧。已经很清楚了。

啦啦啦啦啦。

PPS：命名还是不太好哈，请随便喷我。我一定改正。

最终通过代码

[]
from collections import defaultdict as d

class Solution:
    def findRotateSteps(self, ring: str, key: str) -> int:

        Choices = d()  # 把每个key对应的可选的ring的字母的index做成字典。
        for k in key:
            if k in Choices:
                continue
            else:
                Choices[k] = []
                for ri, r in enumerate(ring):
                    if r == k:
                        Choices[k].append(ri)

        counter = [{0 : 0}]
        Path = d()

        for keyi in range(len(key)): # 一共len(key)个格子。
            counter.append({})
            for choice in Choices[key[keyi]]:  # choice是个index，是表示对于在key上第keyi个字母来说，ring里有哪几个位置的字母可以选择。
                temp = []
                for start in counter[keyi].keys():  # start表示上一个格子里，有几种情况可以到达当前的choice。
                    previous_distance = counter[keyi][start]

                    s = str(start) + "-" + str(choice)
                    if s not in Path:
                        d1 = abs(choice - start)
                        d2 = abs(len(ring) - d1)
                        newc = min(d1, d2)
                        Path[s] = newc

                    temp.append(previous_distance + Path[s])

                counter[keyi + 1][choice] = min(temp) + 1  # 只需要保留最小值  再加1表示按下按钮。

        # print(Choices)
        final = min(counter[-1].values())

        return final

统计信息

通过次数	提交次数	AC比率
20179	40397	50.0%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言