原文链接: https://leetcode-cn.com/problems/kth-smallest-number-in-multiplication-table

英文原文

Nearly everyone has used the Multiplication Table. The multiplication table of size m x n is an integer matrix mat where mat[i][j] == i * j (1-indexed).

Given three integers m, n, and k, return the kth smallest element in the m x n multiplication table.

 

Example 1:

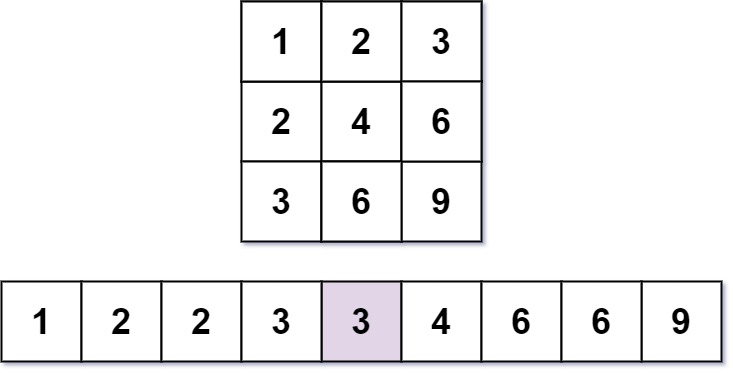
Input: m = 3, n = 3, k = 5
Output: 3
Explanation: The 5th smallest number is 3.

Example 2:

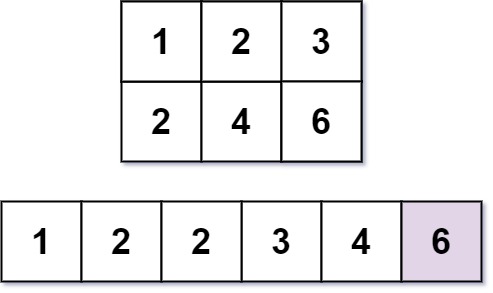
Input: m = 2, n = 3, k = 6
Output: 6
Explanation: The 6th smallest number is 6.

 

Constraints:

• 1 <= m, n <= 3 * 104
• 1 <= k <= m * n

中文题目

几乎每一个人都用 乘法表。但是你能在乘法表中快速找到第k小的数字吗？

给定高度m 、宽度n 的一张 m * n的乘法表，以及正整数k，你需要返回表中第k 小的数字。

例 1：

输入: m = 3, n = 3, k = 5
输出: 3
解释: 
乘法表:
1    2    3
2    4    6
3    6    9

第5小的数字是 3 (1, 2, 2, 3, 3).

例 2：

输入: m = 2, n = 3, k = 6
输出: 6
解释: 
乘法表:
1    2    3
2    4    6

第6小的数字是 6 (1, 2, 2, 3, 4, 6).

注意：

1. m 和 n 的范围在 [1, 30000] 之间。
2. k 的范围在 [1, m * n] 之间。

通过代码

官方题解

方法一：暴力法[超过内存限制]

算法：
创建乘法表并对其排序，然后获取 $k^{th}$ 的元素。

[solution1-Java]
class Solution {
    public int findKthNumber(int m, int n, int k) {
        int[] table = new int[m*n];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                table[(i - 1) * n + j - 1] = i * j;
            }
        }
        Arrays.sort(table);
        return table[k-1];
    }
}

[solution1-Python]
class Solution(object):
    def findKthNumber(self, m, n, k):
        table = [i*j for i in range(1, m+1) for j in range(1, n+1)]
        table.sort()
        return table[k-1]

复杂度分析

• 时间复杂度：$O\big((mn))$ 创建表，然后 $O(mn\log(mn))$ 对其进行排序。
• 空间复杂度：$O(mn)$ 存储乘法表。

方法二：Next Heap[超过时间限制]

算法：

• 维护每行中最小的未使用的元素堆。然后，在堆上查找到下一个元素是一个 pop 操作。
• 我们的堆将由 $\text{(val, root)}$ 组成，其中， $\text{val}$ 是该行的下一个未使用的值，而 $\text{root}$ 是该行的起始值。
• 我们将在表中重复查找下一个最低的元素，若有则堆做一个 pop 弹出一个元素,然后再把表中查到的元素插入堆中。

[solution2-Java]
class Solution {
    public int findKthNumber(int m, int n, int k) {
        PriorityQueue<Node> heap = new PriorityQueue<Node>(m,
            Comparator.<Node> comparingInt(node -> node.val));

        for (int i = 1; i <= m; i++) {
            heap.offer(new Node(i, i));
        }

        Node node = null;
        for (int i = 0; i < k; i++) {
            node = heap.poll();
            int nxt = node.val + node.root;
            if (nxt <= node.root * n) {
                heap.offer(new Node(nxt, node.root));
            }
        }
        return node.val;
    }
}

class Node {
    int val;
    int root;
    public Node(int v, int r) {
        val = v;
        root = r;
    }
}

[solution2-Python]
class Solution(object):
    def findKthNumber(self, m, n, k):
        heap = [(i, i) for i in range(1, m+1)]
        heapq.heapify(heap)

        for _ in xrange(k):
            val, root = heapq.heappop(heap)
            nxt = val + root
            if nxt <= root * n:
                heapq.heappush(heap, (nxt, root))

        return val

复杂度分析

• 时间复杂度：$O(k * m \log m) = O(m^2 n \log m)$。我们最初的操作是 $O(m)$。然后，每个 pop 和 push 都是 $O(m \log m)$ 并且我们的外循环是 $O(k) = O(mn)$
• 空间复杂度：$O(m)$，我们的堆被实现为一个包含 $m$ 元素的数组 。

方法三：二分搜索[通过]

由于 $\text{k}$ 和 $\text{m*n}$ 最多为 $9 * 10^8$，线性解将不起作用。这将激发具有 $\log$ 复杂性的解决方案，例如二分搜索。

算法：
让我们用二分搜索答案 $\text{A}$。

• 当且仅当乘法表中存在小于或等于 $\text{k}$ ，enough(x) 才为真。通俗地说，enough(x) 描述了 $\text{x}$ 是否足够大可以成为乘法表中的 $k^{th}$ 值。
• 然后（对于我们的答案 $\text{A}$），每当 $\text{x ≥ A}$，enough(x) 为 True；每当 $\text{x < A}$，enough(x) 为 False。
• 在二分搜索中，循环不变量 enough(hi) = True。在开始时，enough(m*n) = True，并且每当设置 hi时，都将其设置为“enough”（enough(mi) = True）的值。这意味着 hi 将是二分搜索结束时的最小值。
• 这样我们就可以计算出有多少值小于或等于 $\text{x}$。对于 $\text{m}$ 行中的每一行，$i^{th}$ 行看起来像是 $\text{[i, 2i, 3i, …, ni]}$.。可能出现的最大的 $\text{ki ≤ x}$ 是 $\text{k = x // i}$。但是，如果 $\text{x}$ 真的很大，那么可能是$\text{k > n}$ ，那么在该行中总共有 $\text{min(k, n) = min(x // i, n)}$ 值小于或等于 $\text{x}$ 。

[solution3-Java]
class Solution {
    public boolean enough(int x, int m, int n, int k) {
        int count = 0;
        for (int i = 1; i <= m; i++) {
            count += Math.min(x / i, n);
        }
        return count >= k;
    }

    public int findKthNumber(int m, int n, int k) {
        int lo = 1, hi = m * n;
        while (lo < hi) {
            int mi = lo + (hi - lo) / 2;
            if (!enough(mi, m, n, k)) lo = mi + 1;
            else hi = mi;
        }
        return lo;
    }
}

[solution3-Python]
class Solution(object):
    def findKthNumber(self, m, n, k):
        def enough(x):
            count = 0
            for i in xrange(1, m+1):
                count += min(x // i, n)
            return count >= k

        lo, hi = 1, m * n
        while lo < hi:
            mi = (lo + hi) / 2
            if not enough(mi):
                lo = mi + 1
            else:
                hi = mi
        return lo

复杂度分析

• 时间复杂度：$O(m * \log (mn))$。我们的二分搜索在每一步将间隔 $\text{[lo, hi]}$ 分为两部分。在每个步骤中，我们都调用了 enough，这需要$O(m)$ 时间。
• 空间复杂度：$O(1)$ ,我们只在中间计算期间将整数保存在内存中。

统计信息

通过次数	提交次数	AC比率
7418	14466	51.3%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
有序矩阵中第 K 小的元素	中等
找出第 k 小的距离对	困难
第 K 个最小的素数分数	困难