原文链接: https://leetcode-cn.com/problems/contain-virus

英文原文

A virus is spreading rapidly, and your task is to quarantine the infected area by installing walls.

The world is modeled as an m x n binary grid isInfected, where isInfected[i][j] == 0 represents uninfected cells, and isInfected[i][j] == 1 represents cells contaminated with the virus. A wall (and only one wall) can be installed between any two 4-directionally adjacent cells, on the shared boundary.

Every night, the virus spreads to all neighboring cells in all four directions unless blocked by a wall. Resources are limited. Each day, you can install walls around only one region (i.e., the affected area (continuous block of infected cells) that threatens the most uninfected cells the following night). There will never be a tie.

Return the number of walls used to quarantine all the infected regions. If the world will become fully infected, return the number of walls used.

 

Example 1:

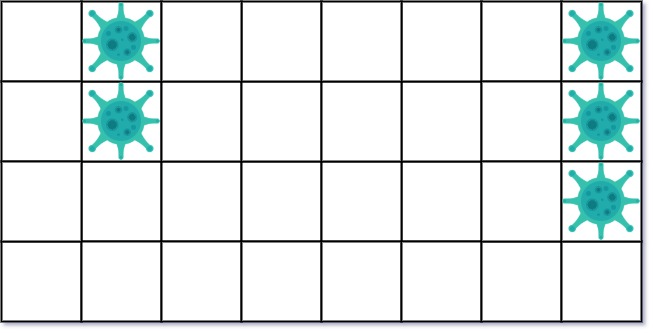
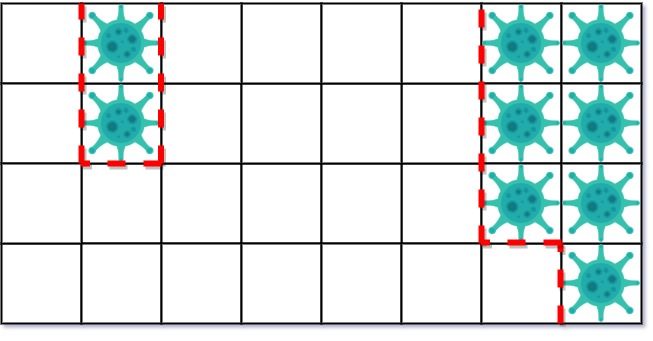
Input: isInfected = [[0,1,0,0,0,0,0,1],[0,1,0,0,0,0,0,1],[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0]]
Output: 10
Explanation: There are 2 contaminated regions.
On the first day, add 5 walls to quarantine the viral region on the left. The board after the virus spreads is:

On the second day, add 5 walls to quarantine the viral region on the right. The virus is fully contained.

Example 2:

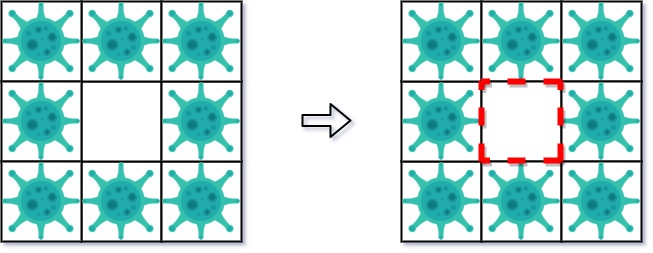
Input: isInfected = [[1,1,1],[1,0,1],[1,1,1]]
Output: 4
Explanation: Even though there is only one cell saved, there are 4 walls built.
Notice that walls are only built on the shared boundary of two different cells.

Example 3:

Input: isInfected = [[1,1,1,0,0,0,0,0,0],[1,0,1,0,1,1,1,1,1],[1,1,1,0,0,0,0,0,0]]
Output: 13
Explanation: The region on the left only builds two new walls.

 

Constraints:

• m == isInfected.length
• n == isInfected[i].length
• 1 <= m, n <= 50
• isInfected[i][j] is either 0 or 1.
• There is always a contiguous viral region throughout the described process that will infect strictly more uncontaminated squares in the next round.

中文题目

病毒扩散得很快，现在你的任务是尽可能地通过安装防火墙来隔离病毒。

假设世界由二维矩阵组成，0 表示该区域未感染病毒，而 1 表示该区域已感染病毒。可以在任意 2 个四方向相邻单元之间的共享边界上安装一个防火墙（并且只有一个防火墙）。

每天晚上，病毒会从被感染区域向相邻未感染区域扩散，除非被防火墙隔离。现由于资源有限，每天你只能安装一系列防火墙来隔离其中一个被病毒感染的区域（一个区域或连续的一片区域），且该感染区域对未感染区域的威胁最大且保证唯一。

你需要努力使得最后有部分区域不被病毒感染，如果可以成功，那么返回需要使用的防火墙个数; 如果无法实现，则返回在世界被病毒全部感染时已安装的防火墙个数。

 

示例 1：

输入: grid = 
[[0,1,0,0,0,0,0,1],
 [0,1,0,0,0,0,0,1],
 [0,0,0,0,0,0,0,1],
 [0,0,0,0,0,0,0,0]]
输出: 10
说明:
一共有两块被病毒感染的区域: 从左往右第一块需要 5 个防火墙，同时若该区域不隔离，晚上将感染 5 个未感染区域（即被威胁的未感染区域个数为 5）;
第二块需要 4 个防火墙，同理被威胁的未感染区域个数是 4。因此，第一天先隔离左边的感染区域，经过一晚后，病毒传播后世界如下:
[[0,1,0,0,0,0,1,1],
 [0,1,0,0,0,0,1,1],
 [0,0,0,0,0,0,1,1],
 [0,0,0,0,0,0,0,1]]
第二题，只剩下一块未隔离的被感染的连续区域，此时需要安装 5 个防火墙，且安装完毕后病毒隔离任务完成。

示例 2：

输入: grid = 
[[1,1,1],
 [1,0,1],
 [1,1,1]]
输出: 4
说明: 
此时只需要安装 4 面防火墙，就有一小区域可以幸存，不被病毒感染。
注意不需要在世界边界建立防火墙。

 

示例 3:

输入: grid = 
[[1,1,1,0,0,0,0,0,0],
 [1,0,1,0,1,1,1,1,1],
 [1,1,1,0,0,0,0,0,0]]
输出: 13
说明: 
在隔离右边感染区域后，隔离左边病毒区域只需要 2 个防火墙了。

 

说明:

1. grid 的行数和列数范围是 [1, 50]。
2.  grid[i][j] 只包含 0 或 1 。
3. 题目保证每次选取感染区域进行隔离时，一定存在唯一一个对未感染区域的威胁最大的区域。

 

通过代码

官方题解

方法：模拟 [Accepted]

让我们来模拟这个过程的一个回合，若仍有感染区域则重复这一步骤。

算法：
虽然实现过程很长，但是算法很简单。我们执行以下步骤：

• 找到所有病毒区域（连续的部分），另外跟踪每个区域的边界（周围未受感染的区域）和该区域的周长。
• 对病毒最多的区域进行隔离，计算所需要的防火墙，将其数量添加到答案中。
• 剩余的病毒向外感染一个区域

[ ]
class Solution(object):
    def containVirus(self, grid):
        R, C = len(grid), len(grid[0])
        def neighbors(r, c):
            for nr, nc in ((r-1, c), (r+1, c), (r, c-1), (r, c+1)):
                if 0 <= nr < R and 0 <= nc < C:
                    yield nr, nc

        def dfs(r, c):
            if (r, c) not in seen:
                seen.add((r, c))
                regions[-1].add((r, c))
                for nr, nc in neighbors(r, c):
                    if grid[nr][nc] == 1:
                        dfs(nr, nc)
                    elif grid[nr][nc] == 0:
                        frontiers[-1].add((nr, nc))
                        perimeters[-1] += 1

        ans = 0
        while True:
            #Find all regions, with associated frontiers and perimeters.
            seen = set()
            regions = []
            frontiers = []
            perimeters = []
            for r, row in enumerate(grid):
                for c, val in enumerate(row):
                    if val == 1 and (r, c) not in seen:
                        regions.append(set())
                        frontiers.append(set())
                        perimeters.append(0)
                        dfs(r, c)

            #If there are no regions left, break.
            if not regions: break

            #Add the perimeter of the region which will infect the most squares.
            triage_index = frontiers.index(max(frontiers, key = len))
            ans += perimeters[triage_index]

            #Triage the most infectious region, and spread the rest of the regions.
            for i, reg in enumerate(regions):
                if i == triage_index:
                    for r, c in reg:
                        grid[r][c] = -1
                else:
                    for r, c in reg:
                        for nr, nc in neighbors(r, c):
                            if grid[nr][nc] == 0:
                                grid[nr][nc] = 1

        return ans

[ ]
class Solution {
    Set<Integer> seen;
    List<Set<Integer>> regions;
    List<Set<Integer>> frontiers;
    List<Integer> perimeters;
    int[][] grid;
    int R, C;
    int[] dr = new int[]{-1, 1, 0, 0};
    int[] dc = new int[]{0, 0, -1, 1};

    public int containVirus(int[][] grid) {
        this.grid = grid;
        R = grid.length;
        C = grid[0].length;

        int ans = 0;
        while (true) {
            seen = new HashSet();
            regions = new ArrayList();
            frontiers = new ArrayList();
            perimeters = new ArrayList();

            for (int r = 0; r < R; ++r) {
                for (int c = 0; c < C; ++c) {
                    if (grid[r][c] == 1 && !seen.contains(r*C + c)) {
                        regions.add(new HashSet());
                        frontiers.add(new HashSet());
                        perimeters.add(0);
                        dfs(r, c);
                    }
                }
            }

            if (regions.isEmpty()) break;
            int triageIndex = 0;
            for (int i = 0; i < frontiers.size(); ++i) {
                if (frontiers.get(triageIndex).size() < frontiers.get(i).size())
                    triageIndex = i;
            }
            ans += perimeters.get(triageIndex);

            for (int i = 0; i < regions.size(); ++i) {
                if (i == triageIndex) {
                    for (int code: regions.get(i))
                        grid[code / C][code % C] = -1;
                } else {
                    for (int code: regions.get(i)) {
                        int r = code / C, c = code % C;
                        for (int k = 0; k < 4; ++k) {
                            int nr = r + dr[k], nc = c + dc[k];
                            if (nr >= 0 && nr < R && nc >= 0 && nc < C && grid[nr][nc] == 0)
                                grid[nr][nc] = 1;
                        }
                    }
                }
            }
        }
        return ans;
    }

    public void dfs(int r, int c) {
        if (!seen.contains(r*C + c)) {
            seen.add(r*C + c);
            int N = regions.size()
            regions.get(N - 1).add(r*C + c);
            for (int k = 0; k < 4; ++k) {
                int nr = r + dr[k], nc = c + dc[k];
                if (nr >= 0 && nr < R && nc >= 0 && nc < C) {
                    if (grid[nr][nc] == 1) {
                        dfs(nr, nc);
                    } else if (grid[nr][nc] == 0){
                        frontiers.get(N - 1).add(nr*C + nc);
                        perimeters.set(N - 1, perimeters.get(N - 1) + 1);
                    }
                }
            }
        }
    }
}

复杂度分析

• 时间复杂度：$O((RC)^{\frac{4}{3}})$。其中 $R, C$ 是矩阵的行和列。在时间 $t$ 之后，存活的病毒区域的大小必须至少为 $t^2 + (t-1)^2$，因此在所有时间内移除的总数为 $\Omega(t^3) \leq RC$。
• 空间复杂度：$O(R*C)$。

统计信息

通过次数	提交次数	AC比率
1503	2994	50.2%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言