原文链接: https://leetcode-cn.com/problems/sliding-puzzle

英文原文

On an 2 x 3 board, there are five tiles labeled from 1 to 5, and an empty square represented by 0. A move consists of choosing 0 and a 4-directionally adjacent number and swapping it.

The state of the board is solved if and only if the board is [[1,2,3],[4,5,0]].

Given the puzzle board board, return the least number of moves required so that the state of the board is solved. If it is impossible for the state of the board to be solved, return -1.

 

Example 1:

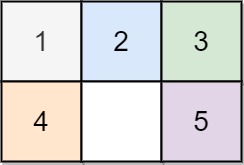
Input: board = [[1,2,3],[4,0,5]]
Output: 1
Explanation: Swap the 0 and the 5 in one move.

Example 2:

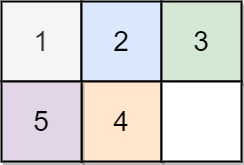
Input: board = [[1,2,3],[5,4,0]]
Output: -1
Explanation: No number of moves will make the board solved.

Example 3:

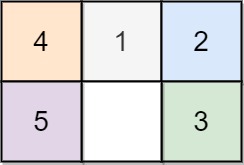
Input: board = [[4,1,2],[5,0,3]]
Output: 5
Explanation: 5 is the smallest number of moves that solves the board.
An example path:
After move 0: [[4,1,2],[5,0,3]]
After move 1: [[4,1,2],[0,5,3]]
After move 2: [[0,1,2],[4,5,3]]
After move 3: [[1,0,2],[4,5,3]]
After move 4: [[1,2,0],[4,5,3]]
After move 5: [[1,2,3],[4,5,0]]

Example 4:

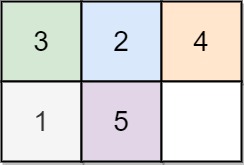
Input: board = [[3,2,4],[1,5,0]]
Output: 14

 

Constraints:

• board.length == 2
• board[i].length == 3
• 0 <= board[i][j] <= 5
• Each value board[i][j] is unique.

中文题目

在一个 2 x 3 的板上（board）有 5 块砖瓦，用数字 1~5 来表示, 以及一块空缺用 0 来表示.

一次移动定义为选择 0 与一个相邻的数字（上下左右）进行交换.

最终当板 board 的结果是 [[1,2,3],[4,5,0]] 谜板被解开。

给出一个谜板的初始状态，返回最少可以通过多少次移动解开谜板，如果不能解开谜板，则返回 -1 。

示例：

输入：board = [[1,2,3],[4,0,5]]
输出：1
解释：交换 0 和 5 ，1 步完成

输入：board = [[1,2,3],[5,4,0]]
输出：-1
解释：没有办法完成谜板

输入：board = [[4,1,2],[5,0,3]]
输出：5
解释：
最少完成谜板的最少移动次数是 5 ，
一种移动路径:
尚未移动: [[4,1,2],[5,0,3]]
移动 1 次: [[4,1,2],[0,5,3]]
移动 2 次: [[0,1,2],[4,5,3]]
移动 3 次: [[1,0,2],[4,5,3]]
移动 4 次: [[1,2,0],[4,5,3]]
移动 5 次: [[1,2,3],[4,5,0]]

输入：board = [[3,2,4],[1,5,0]]
输出：14

提示：

• board 是一个如上所述的 2 x 3 的数组.
• board[i][j] 是一个 [0, 1, 2, 3, 4, 5] 的排列.

通过代码

高赞题解

读完本文，你可以去力扣拿下如下题目：

773.滑动谜题

———–

滑动拼图游戏大家应该都玩过，下图是一个 4x4 的滑动拼图：

{:width=450}{:align=center}

拼图中有一个格子是空的，可以利用这个空着的格子移动其他数字。你需要通过移动这些数字，得到某个特定排列顺序，这样就算赢了。

我小时候还玩过一款叫做「华容道」的益智游戏，也和滑动拼图比较类似：

{:width=450}{:align=center}

那么这种游戏怎么玩呢？我记得是有一些套路的，类似于魔方还原公式。但是我们今天不来研究让人头秃的技巧，这些益智游戏通通可以用暴力搜索算法解决，所以今天我们就学以致用，用 BFS 算法框架来秒杀这些游戏。

一、题目解析

LeetCode 第 773 题就是滑动拼图问题，题目的意思如下：

给你一个 2x3 的滑动拼图，用一个 2x3 的数组 board 表示。拼图中有数字 0~5 六个数，其中数字 0 就表示那个空着的格子，你可以移动其中的数字，当 board 变为 [[1,2,3],[4,5,0]] 时，赢得游戏。

请你写一个算法，计算赢得游戏需要的最少移动次数，如果不能赢得游戏，返回 -1。

比如说输入的二维数组 board = [[4,1,2],[5,0,3]]，算法应该返回 5：

{:width=450}{:align=center}

如果输入的是 board = [[1,2,3],[5,0,4]]，则算法返回 -1，因为这种局面下无论如何都不能赢得游戏。

二、思路分析

对于这种计算最小步数的问题，我们就要敏感地想到 BFS 算法。

这个题目转化成 BFS 问题是有一些技巧的，我们面临如下问题：

1、一般的 BFS 算法，是从一个起点 start 开始，向终点 target 进行寻路，但是拼图问题不是在寻路，而是在不断交换数字，这应该怎么转化成 BFS 算法问题呢？

2、即便这个问题能够转化成 BFS 问题，如何处理起点 start 和终点 target？它们都是数组哎，把数组放进队列，套 BFS 框架，想想就比较麻烦且低效。

首先回答第一个问题，BFS 算法并不只是一个寻路算法，而是一种暴力搜索算法，只要涉及暴力穷举的问题，BFS 就可以用，而且可以最快地找到答案。

你想想计算机怎么解决问题的？哪有那么多奇技淫巧，本质上就是把所有可行解暴力穷举出来，然后从中找到一个最优解罢了。

明白了这个道理，我们的问题就转化成了：如何穷举出 board 当前局面下可能衍生出的所有局面？这就简单了，看数字 0 的位置呗，和上下左右的数字进行交换就行了：

{:width=450}{:align=center}

这样其实就是一个 BFS 问题，每次先找到数字 0，然后和周围的数字进行交换，形成新的局面加入队列…… 当第一次到达 target 时，就得到了赢得游戏的最少步数。

对于第二个问题，我们这里的 board 仅仅是 2x3 的二维数组，所以可以压缩成一个一维字符串。其中比较有技巧性的点在于，二维数组有「上下左右」的概念，压缩成一维后，如何得到某一个索引上下左右的索引？

很简单，我们只要手动写出来这个映射就行了：

vector<vector<int>> neighbor = {
    { 1, 3 },
    { 0, 4, 2 },
    { 1, 5 },
    { 0, 4 },
    { 3, 1, 5 },
    { 4, 2 }
};

**这个含义就是，在一维字符串中，索引 i 在二维数组中的的相邻索引为 neighbor[i]**，：

{:width=450}{:align=center}

至此，我们就把这个问题完全转化成标准的 BFS 问题了，借助前文 BFS 算法框架 的代码框架，直接就可以套出解法代码了：

int slidingPuzzle(vector<vector<int>>& board) {
    int m = 2, n = 3;
    string start = "";
    string target = "123450";
    // 将 2x3 的数组转化成字符串
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            start.push_back(board[i][j] + '0');
        }
    }
    // 记录一维字符串的相邻索引
    vector<vector<int>> neighbor = {
        { 1, 3 },
        { 0, 4, 2 },
        { 1, 5 },
        { 0, 4 },
        { 3, 1, 5 },
        { 4, 2 }
    };
    
    /******* BFS 算法框架开始 *******/
    queue<string> q;
    unordered_set<string> visited;
    q.push(start);
    visited.insert(start);
    
    int step = 0;
    while (!q.empty()) {
        int sz = q.size();
        for (int i = 0; i < sz; i++) {
            string cur = q.front(); q.pop();
            // 判断是否达到目标局面
            if (target == cur) {
                return step;
            }
            // 找到数字 0 的索引
            int idx = 0;
            for (; cur[idx] != '0'; idx++);
            // 将数字 0 和相邻的数字交换位置
            for (int adj : neighbor[idx]) {
                string new_board = cur;
                swap(new_board[adj], new_board[idx]);
                // 防止走回头路
                if (!visited.count(new_board)) {
                    q.push(new_board);
                    visited.insert(new_board);
                }
            }
        }
        step++;
    }
    return -1;
    /******* BFS 算法框架结束 *******/
}

至此，这道题目就解决了，其实框架完全没有变，套路都是一样的，我们只是花了比较多的时间将滑动拼图游戏转化成 BFS 算法。

很多益智游戏都是这样，虽然看起来特别巧妙，但都架不住暴力穷举，常用的算法就是回溯算法或者 BFS 算法。​

＿＿＿＿＿＿＿＿＿＿＿＿＿

点击 我的头像 看更多优质文章。

统计信息

通过次数	提交次数	AC比率
24166	34017	71.0%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言