834-树中距离之和(Sum of Distances in Tree)

原文链接: https://leetcode-cn.com/problems/sum-of-distances-in-tree

英文原文

There is an undirected connected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given the integer n and the array edges where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree.

Return an array answer of length n where answer[i] is the sum of the distances between the i^th node in the tree and all other nodes.

Example 1:

Input: n = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
Output: [8,12,6,10,10,10]
Explanation: The tree is shown above.
We can see that dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5)
equals 1 + 1 + 2 + 2 + 2 = 8.
Hence, answer[0] = 8, and so on.

Example 2:

Input: n = 1, edges = []
Output: [0]

Example 3:

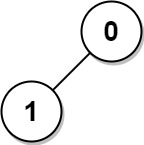
Input: n = 2, edges = [[1,0]]
Output: [1,1]

Constraints:

1 <= n <= 3 * 10⁴
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
The given input represents a valid tree.

中文题目

给定一个无向、连通的树。树中有 N 个标记为 0...N-1 的节点以及 N-1 条边。

第 i 条边连接节点 edges[i][0] 和 edges[i][1] 。

返回一个表示节点 i 与其他所有节点距离之和的列表 ans。

示例 1:

输入: N = 6, edges = [[0,1],[0,2],[2,3],[2,4],[2,5]]
输出: [8,12,6,10,10,10]
解释: 
如下为给定的树的示意图：
  0
 / \
1   2
   /|\
  3 4 5

我们可以计算出 dist(0,1) + dist(0,2) + dist(0,3) + dist(0,4) + dist(0,5) 
也就是 1 + 1 + 2 + 2 + 2 = 8。 因此，answer[0] = 8，以此类推。

说明: 1 <= N <= 10000

通过代码

高赞题解

思路

如上图，其他节点与节点 2 的距离之和，可分为两部分：

节点 2 所在的子树中的节点，与它的距离和。
节点 2 所在的子树之外的节点，与它的距离和。

前者是一个子树内部的问题，可以寻求递归解决——定义distSum[i]：以节点i为根节点的子树中的节点，到节点i的距离和。

如上图，distSum[2]不是它的子节点的distSum简单相加，还要算上走红色路径的次数。

节点 2 到子树 3 中的节点，要走两次红色路径，因为子树 3 有两个节点。

节点 2 到子树 4 中的节点，要走一次红色路径，因为子树 4 有一个节点。

……

因此还要计算每个子树的节点个数nodeNum[i]。写出递归公式：

$$nodeNum[root] = ∑(nodeNum[child])+1$$

$$distSum[root] = ∑(nodeNum[child] + distSum[child])$$

递归到底部就遇到结果已知的case，随着递归的出栈，结果向上返回，就求出了每个子树的distSum。

底部的 base case 就是叶子节点，显然，我们需要遍历当前 root 节点的所有邻居，如果它的邻居只有它的父亲，说明它是叶子节点：nodeNum为 1，distSum为 0。

要想遍历所有的邻居，需要先构建邻接关系表：


const graph = new Array(N);

for (let i = 0; i < graph.length; i++) {

    graph[i] = [];

}

for (const edge of edges) {

    const [from, to] = edge;

    graph[from].push(to);

    graph[to].push(from);

}

先递归压栈压到底，遇到base case，自底而上，由小子树的结果，算出大子树的结果：


const postOrder = (root, parent) => {

    const neighbors = graph[root]; // 与它相连的节点们

    for (const neighbor of neighbors) {

        if (neighbor == parent) {  // 如果邻居是自己父亲，跳过。

            continue;              // 如果邻居只有自己父亲，则for循环结束，当前递归结束  

        }

        postOrder(neighbor, root); // 压栈压到底

        nodeNum[root] += nodeNum[neighbor]; // 两个递归公式

        distSum[root] += nodeNum[neighbor] + distSum[neighbor];

    }

};

—————————————— 分隔符 ————————————————-

节点的distSum，还要加上子树外的节点到它的距离和，才是最后的结果。

后者怎么求？不好求。需要求吗？其实不需要。

对整个树的根节点，它的distSum已经是对的，它的子树就是整棵树，没有子树之外的节点。

我们利用这个正确的distSum，自顶向下推算出它下面节点的真正distSum。

如图，节点2所在的子树的节点个数为nodeNum[2]，从计算distSum[0]变成计算distSum[2]：从节点 0 到这nodeNum[2]个节点，变成从节点 2 到这nodeNum[2]个节点，每个节点都少走了一步，一共少走nodeNum[2]步。

子树以外的节点呢，有N-nodeNum[2]个，从计算distSum[0]变成计算distSum[2]：从节点 0 到这N-nodeNum[2]个，变成从节点 2 到这N-nodeNum[2]个，每个节点都多走了一步，一共多走了N-nodeNum[2]步。

因此子节点distSum[i]与父节点distSum[root]之间的递推关系：

$$distSum[i] = distSum[root] - nodeNum[i] + (N - nodeNum[i])$$

从上往下计算，不是等到遇到底部的 base case 再计算。而是，在递归当前节点的子树之前，就更新当前节点的distSum，使之正确，然后用正确的distSum，递推出子节点的 distSum。

因此先处理当前节点（做计算），再递归压栈，即前序遍历：


const preOrder = (root, parent) => {

    const neighbors = graph[root];

    for (const neighbor of neighbors) {

      if (neighbor == parent) {

        continue;

      }

      distSum[neighbor] = distSum[root] - nodeNum[neighbor] + (N - nodeNum[neighbor]);

      preOrder(neighbor, root);

    }

  };

可见，我们用了两次 DFS，前者计算出每个子树的nodeNum和distSum，后者计算出真正的distSum（每个节点与「其他所有节点」的距离和），注意二者的区别。

最终代码


const sumOfDistancesInTree = (N, edges) => {

  // 建立映射表，graph[i]：存放节点i 和 与它相连的所有节点

  const graph = new Array(N);

  for (let i = 0; i < graph.length; i++) {

    graph[i] = [];

  }

  for (const edge of edges) {

    const [from, to] = edge;

    graph[from].push(to);

    graph[to].push(from);

  }



  // distSum[i]：节点i到它所在子树的节点的距离和，后面更新为：节点i到其他所有节点的距离和

  const distSum = new Array(N).fill(0);

  // nodeNum[i]：节点i所在子树的节点个数，保底为1

  const nodeNum = new Array(N).fill(1);



  const postOrder = (root, parent) => {

    const neighbors = graph[root]; // 与它相连的节点们

    for (const neighbor of neighbors) {

      if (neighbor == parent) {    // 如果邻居是自己父亲，跳过。

        continue;                  // 如果邻居只有自己父亲，则for循环结束，当前递归结束  

      }

      postOrder(neighbor, root);   // 先压栈压到base case，再进行计算

      nodeNum[root] += nodeNum[neighbor]; // 累加计算当前root子树的节点个数

      distSum[root] += nodeNum[neighbor] + distSum[neighbor]; // 累加计算到子树中节点的距离和

    }

  };



  const preOrder = (root, parent) => {

    const neighbors = graph[root]; // 获取当前root节点的邻居

    for (const neighbor of neighbors) { // 遍历邻居

      if (neighbor == parent) {   // 如果邻居是它的父亲，跳过

        continue;                 // 如果邻居只有自己父亲，则for循环结束，当前递归结束

      }

      // 自顶而下 更新子节点们的真正的distSum

      distSum[neighbor] = distSum[root] - nodeNum[neighbor] + (N - nodeNum[neighbor]);

      // 先拿到正确的distSum，再递归压栈（进入子树求更多的distSum）

      preOrder(neighbor, root);

    }

  };



  postOrder(0, -1); // dfs的入口。因为N>=1，节点0肯定存在，就从节点0开始搜

  preOrder(0, -1);

  return distSum;

};

复盘总结

我们复用了distSum数组。它先是代表：节点到它所在子树的节点的距离和。后来代表：节点到其他所有节点的距离和。

当然也可以开辟新的容器去存，毕竟有着不同的定义。但多花了点内存。

本题的突破口依然是：关注当前子树，递归解决，将目标拆分为两部分：

子树内的节点与 root 的距离和
子树外的节点与 root 的距离和

用递归求解前者，后者不用特地求，因为有一个已知的正确的distSum，找出递推关系，从上往下递推出每个节点真正的distSum，就像沿着一棵树在填表，这就是树形DP。

怎么确定父子节点distSum之间的递推关系？

通过比较二者的差别——节点还是这么些个节点，变的部分是什么？一部分多走了一段，剩下部分少走了一段，而且与nodeSum相关，而nodeSum在第一次 dfs 已求得。

我们其实用后序遍历、前序遍历填了三张 DP table：nodeNum,innerDistSum,allDistSum，三个 DP 状态。

使用后序和前序的原因前面有解释，这也是一个值得思考的点。

感谢阅读，点赞更棒。希望我的真诚表述足够清晰，没有一句废话，让你不带着疑惑离开。

最后修改于：2021-10-14

统计信息

通过次数	提交次数	AC比率
13638	25856	52.7%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
在二叉树中分配硬币	中等

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途