847-访问所有节点的最短路径(Shortest Path Visiting All Nodes)

原文链接: https://leetcode-cn.com/problems/shortest-path-visiting-all-nodes

英文原文

You have an undirected, connected graph of n nodes labeled from 0 to n - 1. You are given an array graph where graph[i] is a list of all the nodes connected with node i by an edge.

Return the length of the shortest path that visits every node. You may start and stop at any node, you may revisit nodes multiple times, and you may reuse edges.

Example 1:

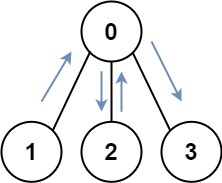
Input: graph = [[1,2,3],[0],[0],[0]]
Output: 4
Explanation: One possible path is [1,0,2,0,3]

Example 2:

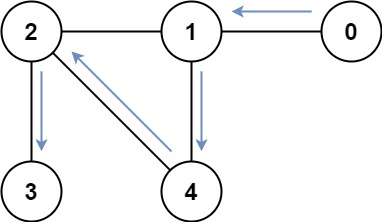
Input: graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
Output: 4
Explanation: One possible path is [0,1,4,2,3]

Constraints:

n == graph.length
1 <= n <= 12
0 <= graph[i].length < n
graph[i] does not contain i.
If graph[a] contains b, then graph[b] contains a.
The input graph is always connected.

中文题目

存在一个由 n 个节点组成的无向连通图，图中的节点按从 0 到 n - 1 编号。

给你一个数组 graph 表示这个图。其中，graph[i] 是一个列表，由所有与节点 i 直接相连的节点组成。

返回能够访问所有节点的最短路径的长度。你可以在任一节点开始和停止，也可以多次重访节点，并且可以重用边。

示例 1：

输入：graph = [[1,2,3],[0],[0],[0]]
输出：4
解释：一种可能的路径为 [1,0,2,0,3]

示例 2：

输入：graph = [[1],[0,2,4],[1,3,4],[2],[1,2]]
输出：4
解释：一种可能的路径为 [0,1,4,2,3]

提示：

n == graph.length
1 <= n <= 12
0 <= graph[i].length < n
graph[i] 不包含 i
如果 graph[a] 包含 b ，那么 graph[b] 也包含 a
输入的图总是连通图

通过代码

高赞题解

本题解共分为 $5$ 个部分，大家可根据自身情况选择性阅读：

旅行商问题的一般形式（简要介绍，可跳过）
广度优先搜索的原理，以及本题为什么可以用广度优先搜索（已经掌握 BFS 的朋友可以跳过）
为什么要利用状态压缩，以及状态压缩是什么？（已经掌握基本状压的朋友可以跳过）
基于状态压缩的广度优先搜索算法
代码

1. 旅行商问题的一般形式

旅行商问题（TSP）：给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。从图论的角度来看，该问题实质是在一个带权完全无向图中，找一个权值最小的哈密顿回路。

本题是一道类似旅行商问题，区别在于：可以重复访问某些节点，且在遍历完最后一个节点后不用回到出发点。

2. 广度优先搜索的原理，以及本题为什么可以用广度优先搜索

广度优先搜索（简称 BFS）算法是一种盲目搜索算法，目的是系统地检查图中所有节点，直到找到结果为止。由于广度优先搜索的扩展原则是先生成的节点先扩展，所以可以求得最短路径。一般而言，利用一个队列 queue 来存储当前已经生成的节点，每次弹出队头元素进行下一步扩展。我们看一个例子：

例子：在以下图中寻找值为 $8$ 的节点

我们首先将起点放入队列，这是第一个生成的节点。

开始第一轮循环，本轮队列中仅 $1$ 个元素。

弹出队头元素 $1$，扩展，生成了 $2, 3$ 两个节点，均放入队列。

队列中 $1$ 个元素扩展完成，本次循环结束。开始新一轮循环，本轮队列中有 $2$ 个元素

弹出队头元素 $2$（因为上一轮先扩展的 $2$），扩展，生成了 $4, 5$ 两个节点，放入队列。

弹出队头元素 $3$，扩展生成 $6, 7$，放入队列。
队列中 $2$ 个元素扩展完成，本次循环结束。开始新一轮循环，本轮队列中有 $4$ 个元素

弹出队头元素 $4$，扩展生成 $8$，找到了答案，当前处在第 $3$ 轮循环，所以最短路径为 $3$。此时本轮仍有 $3$ 个元素未被扩展，但因为已经找到了答案，所以直接退出搜索。

但是 BFS 算法扩展的前提是，每个节点可以以任意顺序扩展，也即一个节点与所有它可以扩展的节点距离都相同。对于本题而言，需要求最短路径，且任意两个节点之间距离均为 $1$，所以可以使用 BFS 算法。

特别地，根据上述例子，我们需要每次记录本轮循环队列中的节点数量，以便最终判定最短路径长度；另一方面，对于已生成的节点，我们需要标记，防止重复被生成。一般而言，为了写代码时更加方便直观，我们在扩展过程中不判断是否找到了答案，而是每次弹出队头元素时进行判断。所以一般的 BFS 代码框架如下：

[]
// 1.初始化队列及标记数组，存入起点
queue<int> q;
vector<bool> vis(n);

q.push(begin_node); // 存入起点，标记
vis[begin_node] = true;

// 2.开始搜索
while(1) {
    int cnt = q.size(); // 本轮需要扩展的节点个数
    if(cnt == 0) break; // 队列中已经没有元素，说明全部节点已经被扩展，退出
    
    // 3.本轮循环
    while(cnt--) {
        int cur = q.front(); // 弹出队头元素
        q.pop();

        // 找到答案，退出搜索
        if(cur == target) break;
        
        action(cur); //有些题目需要对当前元素做处理

        for(int x : cur.children) {
            if(!vis[x]) {
                q.push(x);
                vis[x] = true;
            }
        }
    }

    if(cnt != 0) {
        // 说明本轮未被扩展完，说明找到了目标元素，直接退出搜索
        break;
    }
}

当然，我们也可以将当前扩展的距离作为一个变量一起存入队列：

[]
// 1.初始化队列及标记数组，存入起点
queue<pair<int, int>> q;
vector<bool> vis(n);

q.push({begin_node, 0}); // 存入起点，起始距离0，标记
vis[begin_node] = true;

// 2.开始搜索
while(!q.empty()) {
    auto [cur, dist] = q.front(); // 弹出队头元素
    q.pop();

    // 找到答案，返回结果
    if(cur == target) return dist;
    
    action(cur); //有些题目需要对当前元素做处理

    for(int x : cur.children) {
        if(!vis[x]) {
            q.push({x, dist + 1});
            vis[x] = true;
        }
    }
}

3. 为什么要利用状态压缩，以及状态压缩是什么？

本题与一般的图论题目不同的是，需要遍历完图内全部节点，且可以重复访问某些节点。所以我们需要在搜索过程中，记录当前已经遍历了哪些节点。如果我们利用数组来存储每个节点的状态，在传参时较为不方便，效率不高。本题数据范围 $n \leq 12$，说明可以利用状态压缩。

状态压缩也即用一个变量来表示当前状态，比较常用的方式是利用一个 $n$ 位 $k$ 进制数 $mask$ 表示当前 $n$ 个节点的所处的 $k$ 个不同状态。对于本题而言，某个节点只需要记录是否遍历过，所以利用二进制即可，由于本题数据范围 $n \leq 12$，所以不会超过 int 型范围。

一般而言，$mask$ 从低到高第 $i$ 位为 $0$ 表示第 $i$ 个节点还未被访问过，为 $1$ 则相反。例如，假设有 $3$ 个点，点 $1$ 遍历过，点 $2, 3$ 未遍历，则 $mask = (001)_2$；若点 $3$ 遍历过，点 $1,2$ 未遍历，则 $mask = (100)_2$。特别地，三个点均未遍历时，$mask = (000)_2 = 0$，均遍历过时，$mask = (111)_2 = 2^k - 1$

一些状态压缩的基本操作如下：

（1）访问第 $i$ 个点的状态：state=(1 << i) & mask
（2）更改第 $i$ 个点状态为 $1$：mask = mask | (1 << i)

4. 基于状态压缩的广度优先搜索算法

根据之前的介绍，本题可以通过广度优先搜索算法对图中节点进行扩展，并利用状态压缩记录节点的遍历情况。具体实现细节如下：

BFS 参数：当前节点编号 idx，当前搜索状态 $mask$，当前扩展距离 dist
BFS 起点：题目不限制起点，所以最开始可以将每个点都存入队列，对应状态为仅该点遍历。例如图中有 $2$ 个点时，我们分别将第一个点及其对应的 $mask = (01)_2$，第二个点和其对应的 $mask = (10)_2$ 存入。
BFS 终点：最终要求所有点均遍历，所以当 $mask = 2^n - 1$ 时搜索结束。
BFS 标记：尽管本题可以重复访问某些节点，但是在同一状态下重复访问某一节点必然是无用功。所以在实现时，利用一个二维标记数组记录某一状态下，某一节点的拓展情况，防止被重复扩展。

5. 代码

[]
class Solution {
public:
    int shortestPathLength(vector<vector<int>>& graph) {
        int n = graph.size();

        // 1.初始化队列及标记数组，存入起点
        queue< tuple<int, int, int> > q; // 三个属性分别为 idx, mask, dist
        vector<vector<bool>> vis(n, vector<bool>(1 << n)); // 节点编号及当前状态
        for(int i = 0; i < n; i++) {
            q.push({i, 1 << i, 0}); // 存入起点，起始距离0，标记
            vis[i][1 << i] = true;
        }

        // 开始搜索
        while(!q.empty()) {
            auto [cur, mask, dist] = q.front(); // 弹出队头元素
            q.pop();

            // 找到答案，返回结果
            if(mask == (1 << n) - 1) return dist;

            // 扩展
            for(int x : graph[cur]) {
                int nextmask = mask | (1 << x);
                if(!vis[x][nextmask]) {
                    q.push({x, nextmask, dist + 1});
                    vis[x][nextmask] = true;
                }
            }
        }
        return 0;
    }
};

[]
class Solution {
    public int shortestPathLength(int[][] graph) {
        int n = graph.length;

        // 1.初始化队列及标记数组，存入起点
        Queue<int[]> queue = new LinkedList<int[]>(); // 三个属性分别为 idx, mask, dist
        boolean[][] vis = new boolean[n][1 << n]; // 节点编号及当前状态
        for (int i = 0; i < n; i++) {
            queue.offer(new int[]{i, 1 << i, 0}); // 存入起点，起始距离0，标记
            vis[i][1 << i] = true;
        }

        // 开始搜索
        while (!queue.isEmpty()) {
            int[] tuple = queue.poll(); // 弹出队头元素
            int idx = tuple[0], mask = tuple[1], dist = tuple[2];

            // 找到答案，返回结果
            if (mask == (1 << n) - 1) return dist;
            
            // 扩展
            for (int x : graph[idx]) {
                int next_mask = mask | (1 << x);
                if (!vis[x][next_mask]) {
                    queue.offer(new int[]{x, next_mask, dist + 1});
                    vis[x][next_mask] = true;
                }
            }
        }
        return 0;
    }
}

[]
class Solution:
    def shortestPathLength(self, graph: List[List[int]]) -> int:
        n = len(graph)

        # 1.初始化队列及标记数组，存入起点
        q = deque((i, 1 << i, 0) for i in range(n)) # 三个属性分别为 idx, mask, dist；存入起点，起始距离0，标记
        vis = {(i, 1 << i) for i in range(n)} # 节点编号及当前状态
        
        # 开始搜索
        while q:
            u, mask, dist = q.popleft() # 弹出队头元素
            if mask == (1 << n) - 1: # 找到答案，返回结果
                return dist
            # 扩展
            for x in graph[u]:
                nextmask = mask | (1 << x)
                if (x, nextmask) not in vis:
                    q.append((x, nextmask, dist + 1))
                    vis.add((x, nextmask))
        
        return 0

时间复杂度：$O(n^2*2^n)$

统计信息

通过次数	提交次数	AC比率
19082	28103	67.9%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途