原文链接: https://leetcode-cn.com/problems/rectangle-area-ii

英文原文

You are given a 2D array of axis-aligned rectangles. Each rectangle[i] = [xi1, yi1, xi2, yi2] denotes the ith rectangle where (xi1, yi1) are the coordinates of the bottom-left corner, and (xi2, yi2) are the coordinates of the top-right corner.

Calculate the total area covered by all rectangles in the plane. Any area covered by two or more rectangles should only be counted once.

Return the total area. Since the answer may be too large, return it modulo 109 + 7.

 

Example 1:

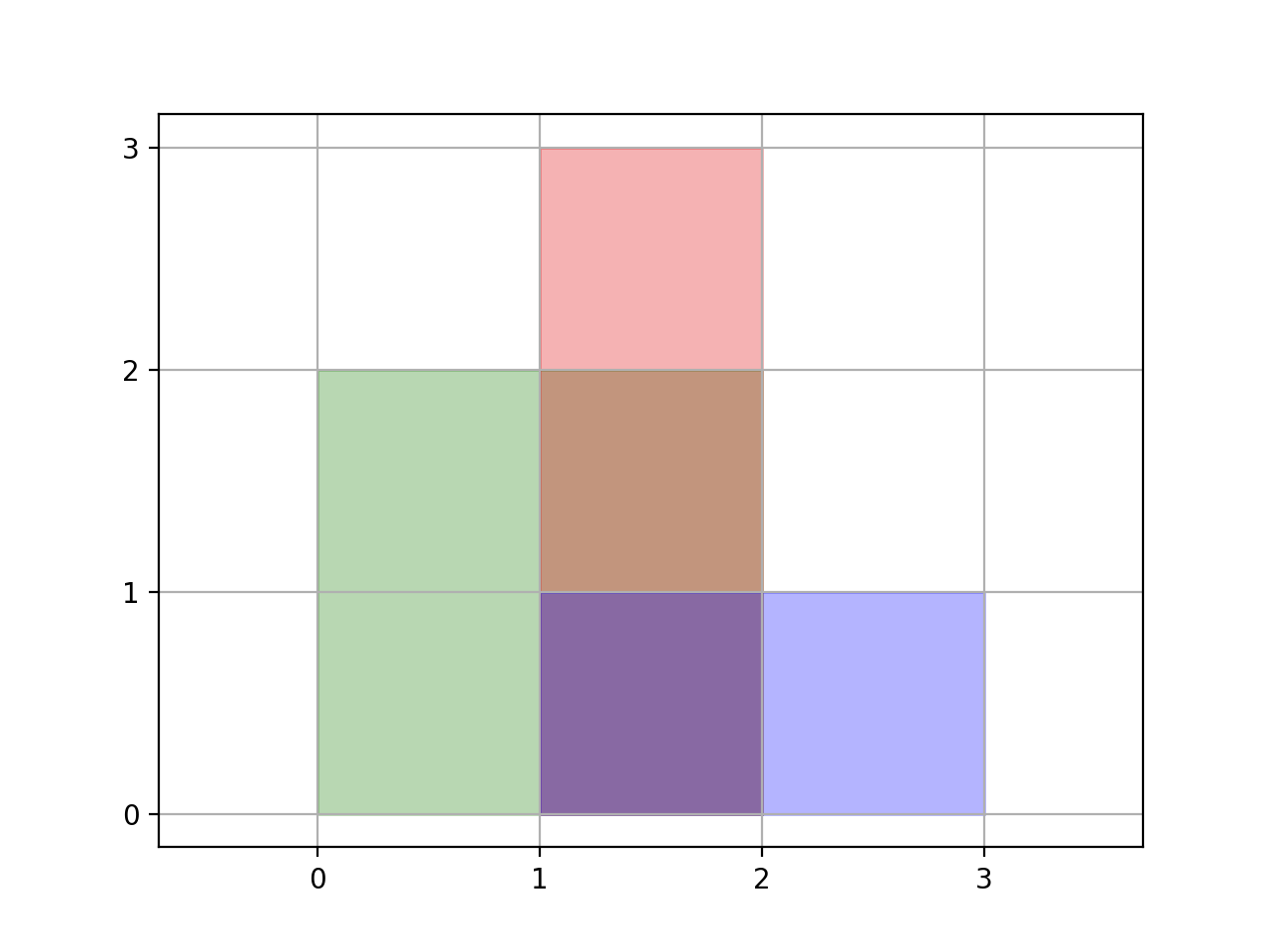
Input: rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
Output: 6
Explanation: A total area of 6 is covered by all three rectangales, as illustrated in the picture.
From (1,1) to (2,2), the green and red rectangles overlap.
From (1,0) to (2,3), all three rectangles overlap.

Example 2:

Input: rectangles = [[0,0,1000000000,1000000000]]
Output: 49
Explanation: The answer is 1018 modulo (109 + 7), which is 49.

 

Constraints:

• 1 <= rectangles.length <= 200
• rectanges[i].length == 4
• 0 <= xi1, yi1, xi2, yi2 <= 109

中文题目

我们给出了一个（轴对齐的）矩形列表 rectangles 。 对于 rectangle[i] = [x1, y1, x2, y2]，其中（x1，y1）是矩形 i 左下角的坐标，（x2，y2）是该矩形右上角的坐标。

找出平面中所有矩形叠加覆盖后的总面积。 由于答案可能太大，请返回它对 10 ^ 9 + 7 取模的结果。

示例 1：

输入：[[0,0,2,2],[1,0,2,3],[1,0,3,1]]
输出：6
解释：如图所示。

示例 2：

输入：[[0,0,1000000000,1000000000]]
输出：49
解释：答案是 10^18 对 (10^9 + 7) 取模的结果， 即 (10^9)^2 → (-7)^2 = 49 。

提示：

• 1 <= rectangles.length <= 200
• rectanges[i].length = 4
• 0 <= rectangles[i][j] <= 10^9
• 矩形叠加覆盖后的总面积不会超越 2^63 - 1 ，这意味着可以用一个 64 位有符号整数来保存面积结果。

通过代码

官方题解

方法一：容斥原理

思路

假设我们有两个矩形 $A$ 和 $B$，它们叠加后覆盖的总面积为：

$$
|A \cup B| = |A| + |B| - |A \cap B|
$$

假设我们有三个矩形 $A, B, C$，它们叠加后覆盖的总面积为：

$$
|A \cup B \cup C| = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C|
$$

假设我们有四个矩形 $A, B, C, D$，它们叠加后覆盖的总面积为：

$$
\begin{align}
|A \cup B \cup C \cup D| =,&\left( |A| + |B| + |C| + |D| \right) - \
,&\left(|A \cap B| + |A \cap C| + |A \cap D| + |B \cap C| + |B \cap D| + |C \cap D|\right) +\
,&\left(|A \cap B \cap C| + |A \cap B \cap D| + |A \cap C \cap D| + |B \cap C \cap D|\right) -\
,&\left(|A \cap B \cap C \cap D|\right)
\end{align}
$$

可以使用维恩图证明这一点。

$n$ 个矩形 $A_1, A_2, \cdots , A_n$ 重叠后的总面积为：

$$
\bigg|\bigcup_{i=1}^n A_i\bigg| = \sum_{\emptyset \neq S \subseteq [n]} (-1)^{|S| + 1} \bigg| \bigcap_{i \in S} A_i \bigg|
$$

算法

如果我们不知道上述原理，可以使用 $\bigg|\bigcup_{i=1}^n A_i\bigg|$ 范围内任意一点验证上述原理的正确性。假设有一点在所有的矩形 $A_i (i \in S)$ 中，并且令 $|S| = n$。在等式右边，该点被计算了 $\binom{n}{1} - \binom{n}{2} + \binom{n}{3} - \cdots \pm \binom{n}{n}$ 次。考虑 $(1 - 1)^n$ 的二项展开，实际上它等于 1。

从矩形面积 I 中可知，两个轴平行矩形的交集要么是一个新的矩形，要么为空。因此 $\bigcap_{i \in S} A_i$ 要么是一个新矩形，要么为空。

算法流程如下：对于 ${1, 2, 3, \cdots, N}$（$N$ 是矩形的数量）的每个子集 $S$，计算该子集的交集 $\bigcap_{i \in S} A_i$ 和它的面积，将结果带入公式得到所有矩形叠加后的覆盖总面积。

[solution1-Java]
class Solution {
    public int rectangleArea(int[][] rectangles) {
        int N = rectangles.length;

        long ans = 0;
        for (int subset = 1; subset < (1<<N); ++subset) {
            int[] rec = new int[]{0, 0, 1_000_000_000, 1_000_000_000};
            int parity = -1;
            for (int bit = 0; bit < N; ++bit)
                if (((subset >> bit) & 1) != 0) {
                    rec = intersect(rec, rectangles[bit]);
                    parity *= -1;
                }
            ans += parity * area(rec);
        }

        long MOD = 1_000_000_007;
        ans %= MOD;
        if (ans < 0) ans += MOD;
        return (int) ans;
    }

    public long area(int[] rec) {
        long dx = Math.max(0, rec[2] - rec[0]);
        long dy = Math.max(0, rec[3] - rec[1]);
        return dx * dy;
    }

    public int[] intersect(int[] rec1, int[] rec2) {
        return new int[]{
            Math.max(rec1[0], rec2[0]),
            Math.max(rec1[1], rec2[1]),
            Math.min(rec1[2], rec2[2]),
            Math.min(rec1[3], rec2[3]),
        };
    }
}

[solution1-Python]
class Solution(object):
    def rectangleArea(self, rectangles):
        def intersect(rec1, rec2):
            return [max(rec1[0], rec2[0]),
                    max(rec1[1], rec2[1]),
                    min(rec1[2], rec2[2]),
                    min(rec1[3], rec2[3])]

        def area(rec):
            dx = max(0, rec[2] - rec[0])
            dy = max(0, rec[3] - rec[1])
            return dx * dy

        ans = 0
        for size in xrange(1, len(rectangles) + 1):
            for group in itertools.combinations(rectangles, size):
                ans += (-1) ** (size + 1) * area(reduce(intersect, group))

        return ans % (10**9 + 7)

复杂度分析

• 时间复杂度：$O(N * 2^N)$，其中 $N$ 是矩形的数量。

• 空间复杂度：$O(N)$。

方法二：坐标压缩

思路

{:width=400}

假设矩形列表为 [[0,0,200,200],[100,0,200,300],[100,0,300,100]]，而不是 rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]，那么答案会扩大 100 倍。

如果矩形列表为 rectangles = [[0,0,2,2],[1,0,2,3],[1,0,30002,1]]，只有蓝色区域的区域的面积为 3000，其他区域均为 1。

我们的思想如下：首先获取所有的 x 和 y 坐标，将它们重新映射到 0, 1, 2, ... 等等。例如将 rectangles = [[0,0,200,200],[100,0,200,300],[100,0,300,100]] 映射到 [[0,0,2,2],[1,0,2,3],[1,0,3,1]]。然后，使用暴力解法计算总覆盖面积。但是因为每个矩形实际上可能表示更大的面积，所以最后需要调整。

算法

将所有 x 和 y 坐标映射到 0, 1, 2, ...。

然后使用暴力解法，在网格上标记每个映射后的矩形。例如对于映射后的矩形 (rx1, ry1, rx2, ry2)，标记满足 rx1 <= x < rx2 且 ry1 <= y < ry2 的网格 grid[x][y] = True。

如果 x 映射得到 rx，则可以通过逆映射 imapy 从 rx 得到 x，即 imapx(rx) = x。每个网格 grid[rx][ry] 代表的实际矩形面积为 (imapx(rx+1) - imapx(rx)) * (imapy(ry+1) - imapy(ry))。

[solution2-Java]
class Solution {
    public int rectangleArea(int[][] rectangles) {
        int N = rectangles.length;
        Set<Integer> Xvals = new HashSet();
        Set<Integer> Yvals = new HashSet();

        for (int[] rec: rectangles) {
            Xvals.add(rec[0]);
            Xvals.add(rec[2]);
            Yvals.add(rec[1]);
            Yvals.add(rec[3]);
        }

        Integer[] imapx = Xvals.toArray(new Integer[0]);
        Arrays.sort(imapx);
        Integer[] imapy = Yvals.toArray(new Integer[0]);
        Arrays.sort(imapy);

        Map<Integer, Integer> mapx = new HashMap();
        Map<Integer, Integer> mapy = new HashMap();
        for (int i = 0; i < imapx.length; ++i)
            mapx.put(imapx[i], i);
        for (int i = 0; i < imapy.length; ++i)
            mapy.put(imapy[i], i);

        boolean[][] grid = new boolean[imapx.length][imapy.length];
        for (int[] rec: rectangles)
            for (int x = mapx.get(rec[0]); x < mapx.get(rec[2]); ++x)
                for (int y = mapy.get(rec[1]); y < mapy.get(rec[3]); ++y)
                    grid[x][y] = true;

        long ans = 0;
        for (int x = 0; x < grid.length; ++x)
            for (int y = 0; y < grid[0].length; ++y)
                if (grid[x][y])
                    ans += (long) (imapx[x+1] - imapx[x]) * (imapy[y+1] - imapy[y]);

        ans %= 1_000_000_007;
        return (int) ans;
    }
}

[solution2-Python]
class Solution(object):
    def rectangleArea(self, rectangles):
        N = len(rectangles)
        Xvals, Yvals = set(), set()
        for x1, y1, x2, y2 in rectangles:
            Xvals.add(x1); Xvals.add(x2)
            Yvals.add(y1); Yvals.add(y2)

        imapx = sorted(Xvals)
        imapy = sorted(Yvals)
        mapx = {x: i for i, x in enumerate(imapx)}
        mapy = {y: i for i, y in enumerate(imapy)}

        grid = [[0] * len(imapy) for _ in imapx]
        for x1, y1, x2, y2 in rectangles:
            for x in xrange(mapx[x1], mapx[x2]):
                for y in xrange(mapy[y1], mapy[y2]):
                    grid[x][y] = 1

        ans = 0
        for x, row in enumerate(grid):
            for y, val in enumerate(row):
                if val:
                    ans += (imapx[x+1] - imapx[x]) * (imapy[y+1] - imapy[y])
        return ans % (10**9 + 7)

复杂度分析

• 时间复杂度：$O(N^3)$，其中 $N$ 是矩形的数量。

• 空间复杂度：$O(N^2)$。

方法三：线性扫描

思想

将每个矩形都看作是一条从底部传递到顶部的水平线段，把从底部到顶部中间的区域称为活动区域，底部边和顶部边称为水平间隔。每个矩形都会更新两次，即在底部添加水平间隔和顶部删除水平间隔。那么 N 个矩形共有 2 * N 次更新，且每次最多更新 N 个水平间隔。

算法

例如矩形 rec = [1,0,3,1]，第一次更新是在 y = 0 时添加水平间隔 [1, 3]，第二次更新是在 y = 1 时删除水平间隔。这里需要注意添加和删除的多重性。如果在 y = 0 时，添加了两条水平间隔 [1, 3] 和 [0, 2]，那么在 y = 1 时只会删除 [1, 3]，不影响 [0, 2]。

为每个矩形创建添加和删除事件，然后以 y 从小到大的顺序处理所有事件。存在一个问题，在处理 add(x1, x2) 和 remove(x1, x2) 事件时如何查询到位于同一 y 坐标的其他水平间隔。

因为 remove(...) 操作总是在 add(...) 之后，因此可以把所有的水平间隔以 y 坐标由小到大的顺序排列。然后使用类似于 LeetCode 合并区间问题实现查询操作 query()。

[solution3-Java]
class Solution {
    public int rectangleArea(int[][] rectangles) {
        int OPEN = 0, CLOSE = 1;
        int[][] events = new int[rectangles.length * 2][];
        int t = 0;
        for (int[] rec: rectangles) {
            events[t++] = new int[]{rec[1], OPEN, rec[0], rec[2]};
            events[t++] = new int[]{rec[3], CLOSE, rec[0], rec[2]};
        }

        Arrays.sort(events, (a, b) -> Integer.compare(a[0], b[0]));

        List<int[]> active = new ArrayList();
        int cur_y = events[0][0];
        long ans = 0;
        for (int[] event: events) {
            int y = event[0], typ = event[1], x1 = event[2], x2 = event[3];

            // Calculate query
            long query = 0;
            int cur = -1;
            for (int[] xs: active) {
                cur = Math.max(cur, xs[0]);
                query += Math.max(xs[1] - cur, 0);
                cur = Math.max(cur, xs[1]);
            }

            ans += query * (y - cur_y);

            if (typ == OPEN) {
                active.add(new int[]{x1, x2});
                Collections.sort(active, (a, b) -> Integer.compare(a[0], b[0]));
            } else {
                for (int i = 0; i < active.size(); ++i)
                    if (active.get(i)[0] == x1 && active.get(i)[1] == x2) {
                        active.remove(i);
                        break;
                    }
            }

            cur_y = y;
        }

        ans %= 1_000_000_007;
        return (int) ans;
    }
}

[solution3-Python]
class Solution(object):
    def rectangleArea(self, rectangles):
        # Populate events
        OPEN, CLOSE = 0, 1
        events = []
        for x1, y1, x2, y2 in rectangles:
            events.append((y1, OPEN, x1, x2))
            events.append((y2, CLOSE, x1, x2))
        events.sort()

        def query():
            ans = 0
            cur = -1
            for x1, x2 in active:
                cur = max(cur, x1)
                ans += max(0, x2 - cur)
                cur = max(cur, x2)
            return ans

        active = []
        cur_y = events[0][0]
        ans = 0
        for y, typ, x1, x2 in events:
            # For all vertical ground covered, update answer
            ans += query() * (y - cur_y)

            # Update active intervals
            if typ is OPEN:
                active.append((x1, x2))
                active.sort()
            else:    
                active.remove((x1, x2))

            cur_y = y

        return ans % (10**9 + 7)

复杂度分析

• 时间复杂度：$O(N^2 \log N)$，其中 $N$ 是矩形的数量。

• 空间复杂度：$O(N)$。

方法四：线段树

思路和算法

为了使用线段树的思想，也需要支持和方法三一样的 add(x1, x2)，remove(x1, x2) 和 query() 操作。

关于更多线段树的知识，可以参考题目：最长递增子序列的个数，掉落的方块。

[solution4-Java]
class Solution {
    public int rectangleArea(int[][] rectangles) {
        int OPEN = 1, CLOSE = -1;
        int[][] events = new int[rectangles.length * 2][];
        Set<Integer> Xvals = new HashSet();
        int t = 0;
        for (int[] rec: rectangles) {
            events[t++] = new int[]{rec[1], OPEN, rec[0], rec[2]};
            events[t++] = new int[]{rec[3], CLOSE, rec[0], rec[2]};
            Xvals.add(rec[0]);
            Xvals.add(rec[2]);
        }

        Arrays.sort(events, (a, b) -> Integer.compare(a[0], b[0]));

        Integer[] X = Xvals.toArray(new Integer[0]);
        Arrays.sort(X);
        Map<Integer, Integer> Xi = new HashMap();
        for (int i = 0; i < X.length; ++i)
            Xi.put(X[i], i);

        Node active = new Node(0, X.length - 1, X);
        long ans = 0;
        long cur_x_sum = 0;
        int cur_y = events[0][0];

        for (int[] event: events) {
            int y = event[0], typ = event[1], x1 = event[2], x2 = event[3];
            ans += cur_x_sum * (y - cur_y);
            cur_x_sum = active.update(Xi.get(x1), Xi.get(x2), typ);
            cur_y = y;

        }

        ans %= 1_000_000_007;
        return (int) ans;
    }
}

class Node {
    int start, end;
    Integer[] X;
    Node left, right;
    int count;
    long total;

    public Node(int start, int end, Integer[] X) {
        this.start = start;
        this.end = end;
        this.X = X;
        left = null;
        right = null;
        count = 0;
        total = 0;
    }

    public int getRangeMid() {
        return start + (end - start) / 2;
    }

    public Node getLeft() {
        if (left == null) left = new Node(start, getRangeMid(), X);
        return left;
    }

    public Node getRight() {
        if (right == null) right = new Node(getRangeMid(), end, X);
        return right;
    }

    public long update(int i, int j, int val) {
        if (i >= j) return 0;
        if (start == i && end == j) {
            count += val;
        } else {
            getLeft().update(i, Math.min(getRangeMid(), j), val);
            getRight().update(Math.max(getRangeMid(), i), j, val);
        }

        if (count > 0) total = X[end] - X[start];
        else total = getLeft().total + getRight().total;

        return total;
    }
}

[solution4-Python]
class Node(object):
    def __init__(self, start, end):
        self.start, self.end = start, end
        self.total = self.count = 0
        self._left = self._right = None

    @property
    def mid(self):
        return (self.start + self.end) / 2

    @property
    def left(self):
        self._left = self._left or Node(self.start, self.mid)
        return self._left

    @property
    def right(self):
        self._right = self._right or Node(self.mid, self.end)
        return self._right

    def update(self, i, j, val):
        if i >= j: return 0
        if self.start == i and self.end == j:
            self.count += val
        else:
            self.left.update(i, min(self.mid, j), val)
            self.right.update(max(self.mid, i), j, val)

        if self.count > 0:
            self.total = X[self.end] - X[self.start]
        else:
            self.total = self.left.total + self.right.total

        return self.total

class Solution(object):
    def rectangleArea(self, rectangles):
        OPEN, CLOSE = 1, -1
        events = []
        global X
        X = set()
        for x1, y1, x2, y2 in rectangles:
            events.append((y1, OPEN, x1, x2))
            events.append((y2, CLOSE, x1, x2))
            X.add(x1)
            X.add(x2)
        events.sort()

        X = sorted(X)
        Xi = {x: i for i, x in enumerate(X)}

        active = Node(0, len(X) - 1)
        ans = 0
        cur_x_sum = 0
        cur_y = events[0][0]

        for y, typ, x1, x2 in events:
            ans += cur_x_sum * (y - cur_y)
            cur_x_sum = active.update(Xi[x1], Xi[x2], typ)
            cur_y = y

        return ans % (10**9 + 7)

复杂度分析

• 时间复杂度：$O(N \log N)$，其中$N$ 是矩形的数量。

• 空间复杂度：$O(N)$。

统计信息

通过次数	提交次数	AC比率
2569	5748	44.7%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言