原文链接: https://leetcode-cn.com/problems/shortest-path-to-get-all-keys

英文原文

You are given an m x n grid grid where:

• '.' is an empty cell.
• '#' is a wall.
• '@' is the starting point.
• Lowercase letters represent keys.
• Uppercase letters represent locks.

You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.

If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.

For some 1 <= k <= 6, there is exactly one lowercase and one uppercase letter of the first k letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.

Return the lowest number of moves to acquire all keys. If it is impossible, return -1.

 

Example 1:

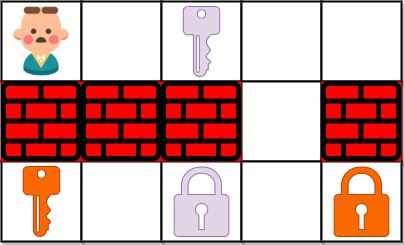
Input: grid = ["@.a.#","###.#","b.A.B"]
Output: 8
Explanation: Note that the goal is to obtain all the keys not to open all the locks.

Example 2:

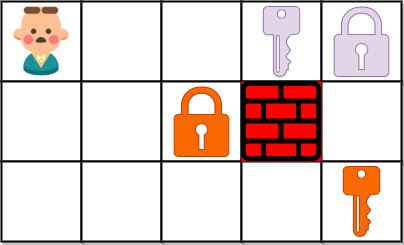
Input: grid = ["@..aA","..B#.","....b"]
Output: 6

Example 3:

Input: grid = ["@Aa"]
Output: -1

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 30
• grid[i][j] is either an English letter, '.', '#', or '@'.
• The number of keys in the grid is in the range [1, 6].
• Each key in the grid is unique.
• Each key in the grid has a matching lock.

中文题目

给定一个二维网格 grid。 "." 代表一个空房间， "#" 代表一堵墙， "@" 是起点，（"a", "b", ...）代表钥匙，（"A", "B", ...）代表锁。

我们从起点开始出发，一次移动是指向四个基本方向之一行走一个单位空间。我们不能在网格外面行走，也无法穿过一堵墙。如果途经一个钥匙，我们就把它捡起来。除非我们手里有对应的钥匙，否则无法通过锁。

假设 K 为钥匙/锁的个数，且满足 1 <= K <= 6，字母表中的前 K 个字母在网格中都有自己对应的一个小写和一个大写字母。换言之，每个锁有唯一对应的钥匙，每个钥匙也有唯一对应的锁。另外，代表钥匙和锁的字母互为大小写并按字母顺序排列。

返回获取所有钥匙所需要的移动的最少次数。如果无法获取所有钥匙，返回 -1 。

 

示例 1：

输入：["@.a.#","###.#","b.A.B"]
输出：8

示例 2：

输入：["@..aA","..B#.","....b"]
输出：6

 

提示：

1. 1 <= grid.length <= 30
2. 1 <= grid[0].length <= 30
3. grid[i][j] 只含有 '.', '#', '@', 'a'-'f' 以及 'A'-'F'
4. 钥匙的数目范围是 [1, 6]，每个钥匙都对应一个不同的字母，正好打开一个对应的锁。

通过代码

官方题解

方法一：暴力 + 枚举

思路和算法

遍历所有可能的获取钥匙的顺序。如果钥匙为 'abcdef'，有一种可能的顺序就是 'bafedc'，之后计算一下这种取法的代价，即 '@' -> 'b' -> 'a' -> 'f' -> 'e' -> 'd' -> 'c' 这条路径的长度。

每取走一把钥匙都需要标记取过的状态，用标记的状态来判断哪些锁可以通过。

[solution1-Java]
import java.awt.Point;

class Solution {
    int INF = Integer.MAX_VALUE;
    String[] grid;
    int R, C;
    Map<Character, Point> location;
    int[] dr = new int[]{-1, 0, 1, 0};
    int[] dc = new int[]{0, -1, 0, 1};

    public int shortestPathAllKeys(String[] grid) {
        this.grid = grid;
        R = grid.length;
        C = grid[0].length();

        //location['a'] = the coordinates of 'a' on the grid, etc.
        location = new HashMap();
        for (int r = 0; r < R; ++r)
            for (int c = 0; c < C; ++c) {
                char v = grid[r].charAt(c);
                if (v != '.' && v != '#')
                    location.put(v, new Point(r, c));
            }

        int ans = INF;
        int num_keys = location.size() / 2;
        String[] alphabet = new String[num_keys];
        for (int i = 0; i < num_keys; ++i)
            alphabet[i] = Character.toString((char)('a' + i));
        //alphabet = ["a", "b", "c"], if there were 3 keys

        search: for (String cand: permutations(alphabet, 0, num_keys)) {
            //bns : the built candidate answer, consisting of the sum
            //of distances of the segments from '@' to cand[0] to cand[1] etc.
            int bns = 0;
            for (int i = 0; i < num_keys; ++i) {
                char source = i > 0 ? cand.charAt(i-1) : '@';
                char target = cand.charAt(i);

                //keymask : an integer with the 0-th bit set if we picked up
                // key 'a', the 1-th bit set if we picked up key 'b', etc.
                int keymask = 0;
                for (int j = 0; j < i; ++j)
                    keymask |= 1 << (cand.charAt(j) - 'a');
                int d = bfs(source, target, keymask);
                if (d == INF) continue search;
                bns += d;
                if (bns >= ans) continue search;
            }
            ans = bns;
        }

        return ans < INF ? ans : -1;
    }

    public int bfs(char source, char target, int keymask) {
        int sr = location.get(source).x;
        int sc = location.get(source).y;
        int tr = location.get(target).x;
        int tc = location.get(target).y;
        boolean[][] seen = new boolean[R][C];
        seen[sr][sc] = true;
        int curDepth = 0;
        Queue<Point> queue = new LinkedList();
        queue.offer(new Point(sr, sc));
        queue.offer(null);

        while (!queue.isEmpty()) {
            Point p = queue.poll();
            if (p == null) {
                curDepth++;
                if (!queue.isEmpty())
                    queue.offer(null);
                continue;
            }
            int r = p.x, c = p.y;
            if (r == tr && c == tc) return curDepth;
            for (int i = 0; i < 4; ++i) {
                int cr = r + dr[i];
                int cc = c + dc[i];
                if (0 <= cr && cr < R && 0 <= cc && cc < C && !seen[cr][cc]){
                    char cur = grid[cr].charAt(cc);
                    if (cur != '#') {
                        if (Character.isUpperCase(cur) && (((1 << (cur - 'A')) & keymask) <= 0))
                            continue; // at lock and don't have key

                        queue.offer(new Point(cr, cc));
                        seen[cr][cc] = true;
                    }
                }
            }
        }

        return INF;
    }

    public List<String> permutations(String[] alphabet, int used, int size) {
        List<String> ans = new ArrayList();
        if (size == 0) {
            ans.add(new String(""));
            return ans;
        }

        for (int b = 0; b < alphabet.length; ++b)
            if (((used >> b) & 1) == 0)
                for (String rest: permutations(alphabet, used | (1 << b), size - 1))
                    ans.add(alphabet[b] + rest);
        return ans;
    }
}

[solution1-Python]
class Solution(object):
    def shortestPathAllKeys(self, grid):
        R, C = len(grid), len(grid[0])
        # location['a'] = the coordinates of 'a' on the grid, etc.
        location = {v: (r, c)
                    for r, row in enumerate(grid)
                    for c, v in enumerate(row)
                    if v not in '.#'}

        def neighbors(r, c):
            for cr, cc in ((r-1, c), (r, c-1), (r+1, c), (r, c+1)):
                if 0 <= cr < R and 0 <= cc < C:
                    yield cr, cc

        def bfs(source, target, keys = ()):
            sr, sc = location[source]
            tr, tc = location[target]
            seen = [[False] * C for _ in xrange(R)]
            seen[sr][sc] = True
            queue = collections.deque([(sr, sc, 0)])
            while queue:
                r, c, d = queue.popleft()
                if r == tr and c == tc: return d
                for cr, cc in neighbors(r, c):
                    if not seen[cr][cc] and grid[cr][cc] != '#':
                        if grid[cr][cc].isupper() and grid[cr][cc].lower() not in keys:
                            continue
                        queue.append((cr,cc,d+1))
                        seen[cr][cc] = True
            return float('inf')

        ans = float('inf')
        keys = "".join(chr(ord('a') + i) for i in xrange(len(location) / 2))
        for cand in itertools.permutations(keys):
            # bns : the built candidate answer, consisting of the sum
            # of distances of the segments from '@' to cand[0] to cand[1] etc.
            bns = 0
            for i, target in enumerate(cand):
                source = cand[i-1] if i > 0 else '@'
                d = bfs(source, target, cand[:i])
                bns += d
                if bns >= ans: break
            else:
                ans = bns

        return ans if ans < float('inf') else -1

复杂度分析

• 时间复杂度： $O(R * C * A * A!)$，其中 $R, C$ 为表格的长宽，（$A$ 为钥匙的数量）。深度优先搜索最多执行 $A * A!$ 次。

• 空间复杂度： $O(R * C + A!)$，$R * C$ 为深度优先搜索占用的空间，$A！$ 为全排序数组占用的空间。

方法二： 关键点 + Dijkstra

思路和算法

显然钥匙，锁，起点是图中的关键节点。先用深度优先搜索计算所有关键节点之间的距离，再用Dijkstra 算法找到每一种状态下的最小代价。

[solution2-Java]
import java.awt.Point;

class Solution {
    int INF = Integer.MAX_VALUE;
    String[] grid;
    int R, C;
    Map<Character, Point> location;
    int[] dr = new int[]{-1, 0, 1, 0};
    int[] dc = new int[]{0, -1, 0, 1};

    public int shortestPathAllKeys(String[] grid) {
        this.grid = grid;
        R = grid.length;
        C = grid[0].length();

        //location : the points of interest
        location = new HashMap();
        for (int r = 0; r < R; ++r)
            for (int c = 0; c < C; ++c) {
                char v = grid[r].charAt(c);
                if (v != '.' && v != '#')
                    location.put(v, new Point(r, c));
            }

        int targetState = (1 << (location.size() / 2)) - 1;
        Map<Character, Map<Character, Integer>> dists = new HashMap();
        for (char place: location.keySet())
            dists.put(place, bfsFrom(place));

        //Dijkstra
        PriorityQueue<ANode> pq = new PriorityQueue<ANode>((a, b) ->
                Integer.compare(a.dist, b.dist));
        pq.offer(new ANode(new Node('@', 0), 0));
        Map<Node, Integer> finalDist = new HashMap();
        finalDist.put(new Node('@', 0), 0);

        while (!pq.isEmpty()) {
            ANode anode = pq.poll();
            Node node = anode.node;
            int d = anode.dist;
            if (finalDist.getOrDefault(node, INF) < d) continue;
            if (node.state == targetState) return d;

            for (char destination: dists.get(node.place).keySet()) {
                int d2 = dists.get(node.place).get(destination);
                int state2 = node.state;
                if (Character.isLowerCase(destination)) //key
                    state2 |= (1 << (destination - 'a'));
                if (Character.isUpperCase(destination)) //lock
                    if ((node.state & (1 << (destination - 'A'))) == 0) // no key
                        continue;

                if (d + d2 < finalDist.getOrDefault(new Node(destination, state2), INF)) {
                    finalDist.put(new Node(destination, state2), d + d2);
                    pq.offer(new ANode(new Node(destination, state2), d+d2));
                }
            }
        }

        return -1;
    }

    public Map<Character, Integer> bfsFrom(char source) {
        int sr = location.get(source).x;
        int sc = location.get(source).y;
        boolean[][] seen = new boolean[R][C];
        seen[sr][sc] = true;
        int curDepth = 0;
        Queue<Point> queue = new LinkedList();
        queue.offer(new Point(sr, sc));
        queue.offer(null);
        Map<Character, Integer> dist = new HashMap();

        while (!queue.isEmpty()) {
            Point p = queue.poll();
            if (p == null) {
                curDepth++;
                if (!queue.isEmpty())
                    queue.offer(null);
                continue;
            }

            int r = p.x, c = p.y;
            if (grid[r].charAt(c) != source && grid[r].charAt(c) != '.') {
                dist.put(grid[r].charAt(c), curDepth);
                continue; // Stop walking from here if we reach a point of interest
            }

            for (int i = 0; i < 4; ++i) {
                int cr = r + dr[i];
                int cc = c + dc[i];
                if (0 <= cr && cr < R && 0 <= cc && cc < C && !seen[cr][cc]){
                    if (grid[cr].charAt(cc) != '#') {
                        queue.offer(new Point(cr, cc));
                        seen[cr][cc] = true;
                    }
                }
            }
        }

        return dist;
    }
}

// ANode: Annotated Node
class ANode {
    Node node;
    int dist;

    ANode(Node n, int d) {
        node = n;
        dist = d;
    }
}

class Node {
    char place;
    int state;

    Node(char p, int s) {
        place = p;
        state = s;
    }

    @Override
    public boolean equals(Object o) {
        if (this == o) return true;
        if (!(o instanceof Node)) return false;
        Node other = (Node) o;
        return (place == other.place && state == other.state);
    }

    @Override
    public int hashCode() {
        return 256 * state + place;
    }
}

[solution2-Python]
class Solution(object):
    def shortestPathAllKeys(self, grid):
        R, C = len(grid), len(grid[0])

        # The points of interest
        location = {v: (r, c)
                    for r, row in enumerate(grid)
                    for c, v in enumerate(row)
                    if v not in '.#'}

        def neighbors(r, c):
            for cr, cc in ((r-1, c), (r, c-1), (r+1, c), (r, c+1)):
                if 0 <= cr < R and 0 <= cc < C:
                    yield cr, cc

        # The distance from source to each point of interest
        def bfs_from(source):
            r, c = location[source]
            seen = [[False] * C for _ in xrange(R)]
            seen[r][c] = True
            queue = collections.deque([(r, c, 0)])
            dist = {}
            while queue:
                r, c, d = queue.popleft()
                if source != grid[r][c] != '.':
                    dist[grid[r][c]] = d
                    continue # Stop walking from here if we reach a point of interest
                for cr, cc in neighbors(r, c):
                    if grid[cr][cc] != '#' and not seen[cr][cc]:
                        seen[cr][cc] = True
                        queue.append((cr, cc, d+1))
            return dist        

        dists = {place: bfs_from(place) for place in location}
        target_state = 2 ** sum(p.islower() for p in location) - 1

        #Dijkstra
        pq = [(0, '@', 0)]
        final_dist = collections.defaultdict(lambda: float('inf'))
        final_dist['@', 0] = 0
        while pq:
            d, place, state = heapq.heappop(pq)
            if final_dist[place, state] < d: continue
            if state == target_state: return d
            for destination, d2 in dists[place].iteritems():
                state2 = state
                if destination.islower(): #key
                    state2 |= (1 << (ord(destination) - ord('a')))
                elif destination.isupper(): #lock
                    if not(state & (1 << (ord(destination) - ord('A')))): #no key
                        continue

                if d + d2 < final_dist[destination, state2]:
                    final_dist[destination, state2] = d + d2
                    heapq.heappush(pq, (d+d2, destination, state2))

        return -1

复杂度分析

• 时间复杂度： $O(RC(2A + 1) + E\log{N})$，其中 $R, C$ 是表格的长宽， $A$ 为钥匙总数，$RC(2A + 1$ 为深度优先遍历的复杂度。$N = (2A + 1) * 2^A$ 为 Dijkstra 遍历最大节点数，$E = N * (2A + 1)$ 为 Dijkstra 遍历最大边数，$E\log{N}$ 为 Dijkstra 算法复杂度。

统计信息

通过次数	提交次数	AC比率
3181	6936	45.9%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言