英文原文
A game on an undirected graph is played by two players, Mouse and Cat, who alternate turns.
The graph is given as follows: graph[a] is a list of all nodes b such that ab is an edge of the graph.
The mouse starts at node 1 and goes first, the cat starts at node 2 and goes second, and there is a hole at node 0.
During each player's turn, they must travel along one edge of the graph that meets where they are. For example, if the Mouse is at node 1, it must travel to any node in graph[1].
Additionally, it is not allowed for the Cat to travel to the Hole (node 0.)
Then, the game can end in three ways:
- If ever the Cat occupies the same node as the Mouse, the Cat wins.
- If ever the Mouse reaches the Hole, the Mouse wins.
- If ever a position is repeated (i.e., the players are in the same position as a previous turn, and it is the same player's turn to move), the game is a draw.
Given a graph, and assuming both players play optimally, return
1if the mouse wins the game,2if the cat wins the game, or0if the game is a draw.
Example 1:
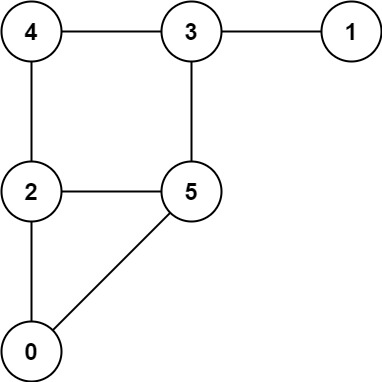
Input: graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]] Output: 0
Example 2:
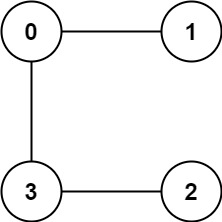
Input: graph = [[1,3],[0],[3],[0,2]] Output: 1
Constraints:
3 <= graph.length <= 501 <= graph[i].length < graph.length0 <= graph[i][j] < graph.lengthgraph[i][j] != igraph[i]is unique.- The mouse and the cat can always move.
中文题目
两个玩家分别扮演猫(Cat)和老鼠(Mouse)在无向图上进行游戏,他们轮流行动。
该图按下述规则给出:graph[a] 是所有结点 b 的列表,使得 ab 是图的一条边。
老鼠从结点 1 开始并率先出发,猫从结点 2 开始且随后出发,在结点 0 处有一个洞。
在每个玩家的回合中,他们必须沿着与他们所在位置相吻合的图的一条边移动。例如,如果老鼠位于结点 1,那么它只能移动到 graph[1] 中的(任何)结点去。
此外,猫无法移动到洞(结点 0)里。
然后,游戏在出现以下三种情形之一时结束:
- 如果猫和老鼠占据相同的结点,猫获胜。
- 如果老鼠躲入洞里,老鼠获胜。
- 如果某一位置重复出现(即,玩家们的位置和移动顺序都与上一个回合相同),游戏平局。
给定 graph,并假设两个玩家都以最佳状态参与游戏,如果老鼠获胜,则返回 1;如果猫获胜,则返回 2;如果平局,则返回 0。
示例:
输入:[[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]] 输出:0 解释: 4---3---1 | | 2---5 \ / 0
提示:
3 <= graph.length <= 200- 保证
graph[1]非空。 - 保证
graph[2]包含非零元素。
通过代码
官方题解
方法 1:极大极小 / 从已知状态分析
想法
游戏的状态可以表示成 (m, c, t),其中 m 是老鼠的位置,c 是猫的位置,t 当老鼠移动为 1 猫移动为 2。我们把这些状态看成节点,状态集合构成了一个有向图:玩家每一轮都有若干种选择方案,对应一个节点到另一个节点的有向边。
有些节点的结果已经固定了:当老鼠位于洞时 (m = 0) 老鼠获胜;如果猫和老鼠重合 (c = m) 猫获胜。认定节点会根据玩家胜利情况被定义成 $\small\text{MOUSE}$,$\small\text{CAT}$,$\small\text{DRAW}$。
根据标准的极大极小算法,老鼠玩家倾向于首先移动到 $\small\text{MOUSE}$ 节点,其次是 $\small\text{DRAW}$ 节点,最后是 $\small\text{CAT}$ 节点。猫玩家的倾向顺序恰好相反。
算法
我们对每个节点 node 依据以下规则标记成 $\small\text{DRAW}$。(假设 node.turn = Mouse:另一种情况类似)
- 立即染色:如果存在一个孩子标记成 $\small\text{MOUSE}$,那么这个节点会被染成 $\small\text{MOUSE}$。
- 最终染色:如果所有孩子标记成 $\small\text{CAT}$,那么这个节点也会被染成 $\small\text{CAT}$。
我们重复如下操作直至没有 node 节点满足条件。为了让这种染色更为高效,我们会使用一个队列执行自底向上的渗透:
- 入队所有已经初始化染色的顶点(因为老鼠在洞中或者猫和老鼠在一个位置)。
- 对于队列中的每一个顶点
node,所有node的父亲parent:- 对满足条件的
parent做立即染色; - 如果不行,减少标记成 $\small\text{DRAW}$ 的孩子边数,当边数减少到 0 时执行最终染色;
- 所有染色的
parent加入队列中。
- 对满足条件的
正确性证明
我们的证明与极大极小算法的证明类似。
假如不能再对节点染色,并且任何标记成 $\small\text{CAT}$ 或者 $\small\text{MOUSE}$ 的节点需要最多 $K$ 步取胜。那么,如果对于一个标记为 $\small\text{DRAW}$ 的顶点实际上是老鼠获胜,那么一定需要 $> K$ 步。一条最优路径最终一定会到达一个标记为 $\small\text{MOUSE}$ 的点(因为老鼠会到达洞内)。因此,一定有一条 $\small\text{DRAW} \rightarrow \small\text{MOUSE}$ 的可行路径。
如果这一步发生在老鼠的回合,那么可以使用立即染色规则。如果发生在猫的回合,并且所有孩子节点都是 $\small\text{MOUSE}$,那么可以使用最终染色规则;如果一些节点是 $\small\text{CAT}$,那么也会利用最终染色规则。因此,只剩下一些节点为 $\small\text{DRAW}$,根据我们最优路径的假设,移动到这些节点结束需要 $> K$ 步,然而移动到标记邻居的步骤只需要 $\leq K$ 步,不存在这样的路径,所以是平局。
[]class Solution { public int catMouseGame(int[][] graph) { int N = graph.length; final int DRAW = 0, MOUSE = 1, CAT = 2; int[][][] color = new int[50][50][3]; int[][][] degree = new int[50][50][3]; // degree[node] : the number of neutral children of this node for (int m = 0; m < N; ++m) for (int c = 0; c < N; ++c) { degree[m][c][1] = graph[m].length; degree[m][c][2] = graph[c].length; for (int x: graph[c]) if (x == 0) { degree[m][c][2]--; break; } } // enqueued : all nodes that are colored Queue<int[]> queue = new LinkedList(); for (int i = 0; i < N; ++i) for (int t = 1; t <= 2; ++t) { color[0][i][t] = MOUSE; queue.add(new int[]{0, i, t, MOUSE}); if (i > 0) { color[i][i][t] = CAT; queue.add(new int[]{i, i, t, CAT}); } } // percolate while (!queue.isEmpty()) { // for nodes that are colored : int[] node = queue.remove(); int i = node[0], j = node[1], t = node[2], c = node[3]; // for every parent of this node i, j, t : for (int[] parent: parents(graph, i, j, t)) { int i2 = parent[0], j2 = parent[1], t2 = parent[2]; // if this parent is not colored : if (color[i2][j2][t2] == DRAW) { // if the parent can make a winning move (ie. mouse to MOUSE), do so if (t2 == c) { color[i2][j2][t2] = c; queue.add(new int[]{i2, j2, t2, c}); } else { // else, this parent has degree[parent]--, and enqueue // if all children of this parent are colored as losing moves degree[i2][j2][t2]--; if (degree[i2][j2][t2] == 0) { color[i2][j2][t2] = 3 - t2; queue.add(new int[]{i2, j2, t2, 3 - t2}); } } } } } return color[1][2][1]; } // What nodes could play their turn to // arrive at node (m, c, t) ? public List<int[]> parents(int[][] graph, int m, int c, int t) { List<int[]> ans = new ArrayList(); if (t == 2) { for (int m2: graph[m]) ans.add(new int[]{m2, c, 3-t}); } else { for (int c2: graph[c]) if (c2 > 0) ans.add(new int[]{m, c2, 3-t}); } return ans; } }
[]class Solution(object): def catMouseGame(self, graph): N = len(graph) # What nodes could play their turn to # arrive at node (m, c, t) ? def parents(m, c, t): if t == 2: for m2 in graph[m]: yield m2, c, 3-t else: for c2 in graph[c]: if c2: yield m, c2, 3-t DRAW, MOUSE, CAT = 0, 1, 2 color = collections.defaultdict(int) # degree[node] : the number of neutral children of this node degree = {} for m in xrange(N): for c in xrange(N): degree[m,c,1] = len(graph[m]) degree[m,c,2] = len(graph[c]) - (0 in graph[c]) # enqueued : all nodes that are colored queue = collections.deque([]) for i in xrange(N): for t in xrange(1, 3): color[0, i, t] = MOUSE queue.append((0, i, t, MOUSE)) if i > 0: color[i, i, t] = CAT queue.append((i, i, t, CAT)) # percolate while queue: # for nodes that are colored : i, j, t, c = queue.popleft() # for every parent of this node i, j, t : for i2, j2, t2 in parents(i, j, t): # if this parent is not colored : if color[i2, j2, t2] is DRAW: # if the parent can make a winning move (ie. mouse to MOUSE), do so if t2 == c: # winning move color[i2, j2, t2] = c queue.append((i2, j2, t2, c)) # else, this parent has degree[parent]--, and enqueue if all children # of this parent are colored as losing moves else: degree[i2, j2, t2] -= 1 if degree[i2, j2, t2] == 0: color[i2, j2, t2] = 3 - t2 queue.append((i2, j2, t2, 3 - t2)) return color[1, 2, 1]
复杂度分析
- 时间复杂度:$O(N^3)$,其中 $N$ 是图中节点的数量,总共有 $O(N^2)$ 种状态,每一个状态节点最多有 $N$ 个出边,也就是 $N$ 种不同的移动方法。
- 空间复杂度:$O(N^2)$。
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 1988 | 4964 | 40.0% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




