原文链接: https://leetcode-cn.com/problems/largest-component-size-by-common-factor

英文原文

You are given an integer array of unique positive integers nums. Consider the following graph:

• There are nums.length nodes, labeled nums[0] to nums[nums.length - 1],
• There is an undirected edge between nums[i] and nums[j] if nums[i] and nums[j] share a common factor greater than 1.

Return the size of the largest connected component in the graph.

 

Example 1:

Input: nums = [4,6,15,35]
Output: 4

Example 2:

Input: nums = [20,50,9,63]
Output: 2

Example 3:

Input: nums = [2,3,6,7,4,12,21,39]
Output: 8

 

Constraints:

• 1 <= nums.length <= 2 * 104
• 1 <= nums[i] <= 105
• All the values of nums are unique.

中文题目

给定一个由不同正整数的组成的非空数组 A，考虑下面的图：

• 有 A.length 个节点，按从 A[0] 到 A[A.length - 1] 标记；
• 只有当 A[i] 和 A[j] 共用一个大于 1 的公因数时，A[i] 和 A[j] 之间才有一条边。

返回图中最大连通组件的大小。

 

示例 1：

输入：[4,6,15,35]
输出：4

示例 2：

输入：[20,50,9,63]
输出：2

示例 3：

输入：[2,3,6,7,4,12,21,39]
输出：8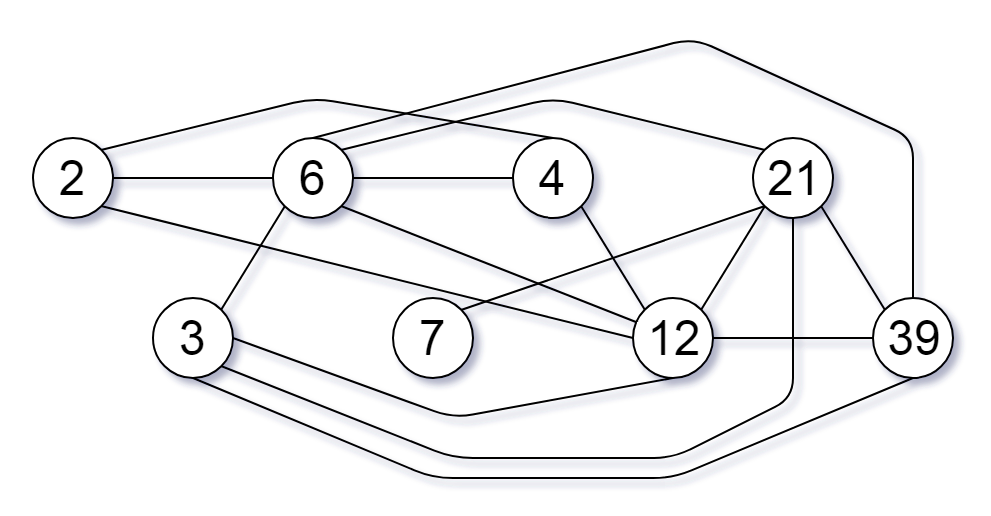

 

提示：

1. 1 <= A.length <= 20000
2. 1 <= A[i] <= 100000

通过代码

官方题解

方法一： 并查集

思路

设 $W = \max(A[i])$，$R = \sqrt{W}$。对于数组 $A$ 中的每个数，最多只有一个非本身的质因数 $p$ 满足 $p \geq R$。

这就意味着最多只有 $R + A\text{.length}$ 个不同的质因数： 为本身的质因数最多有 $A\text{.length}$ 个，非本身的质因数一定比 $R$ 小，最多有 $R$ 个。

算法

提取数组 $A$ 中每个数的质因数，对每个质因数建立索引。接着，用并查集把 $A$ 中的质因数合并起来。最后计算每个集合的大小。

[solution1-Java]
class Solution {
    public int largestComponentSize(int[] A) {
        int N = A.length;

        // factored[i] = a list of unique prime factors of A[i]
        ArrayList<Integer>[] factored = new ArrayList[N];
        for (int i = 0; i < N; ++i) {
            factored[i] = new ArrayList<Integer>();
            int d = 2, x = A[i];
            while (d * d <= x) {
                if (x % d == 0) {
                    while (x % d == 0)
                        x /= d;
                    factored[i].add(d);
                }

                d++;
            }

            if (x > 1 || factored[i].isEmpty())
                factored[i].add(x);
        }

        // primesL : a list of all primes that occur in factored
        Set<Integer> primes = new HashSet();
        for (List<Integer> facs: factored)
            for (int x: facs)
                primes.add(x);

        int[] primesL = new int[primes.size()];
        int t = 0;
        for (int x: primes)
            primesL[t++] = x;

        // primeToIndex.get(v) == i  iff  primes[i] = v
        Map<Integer, Integer> primeToIndex = new HashMap();
        for (int i = 0; i < primesL.length; ++i)
            primeToIndex.put(primesL[i], i);

        DSU dsu = new DSU(primesL.length);
        for (List<Integer> facs: factored)
            for (int x: facs)
                dsu.union(primeToIndex.get(facs.get(0)), primeToIndex.get(x));

        int[] count = new int[primesL.length];
        for (List<Integer> facs: factored)
            count[dsu.find(primeToIndex.get(facs.get(0)))]++;

        int ans = 0;
        for (int x: count)
            if (x > ans)
                ans = x;
        return ans;
    }
}

class DSU {
    int[] parent;
    public DSU(int N) {
        parent = new int[N];
        for (int i = 0; i < N; ++i)
            parent[i] = i;
    }
    public int find(int x) {
        if (parent[x] != x) parent[x] = find(parent[x]);
        return parent[x];
    }
    public void union(int x, int y) {
        parent[find(x)] = find(y);
    }
}

[solution1-Python]
class DSU:
    def __init__(self, N):
        self.p = range(N)

    def find(self, x):
        if self.p[x] != x:
            self.p[x] = self.find(self.p[x])
        return self.p[x]

    def union(self, x, y):
        xr = self.find(x)
        yr = self.find(y)
        self.p[xr] = yr

class Solution(object):
    def largestComponentSize(self, A):
        B = []
        for x in A:
            facs = []
            d = 2
            while d * d <= x:
                if x % d == 0:
                    while x % d == 0:
                        x /= d
                    facs.append(d)
                d += 1

            if x > 1 or not facs:
                facs.append(x)
            B.append(facs)

        primes = list({p for facs in B for p in facs})
        prime_to_index = {p: i for i, p in enumerate(primes)}

        dsu = DSU(len(primes))
        for facs in B:
            for x in facs:
                dsu.union(prime_to_index[facs[0]], prime_to_index[x])

        count = collections.Counter(dsu.find(prime_to_index[facs[0]]) for facs in B)
        return max(count.values())

复杂度分析

• 时间复杂度： $O(N\sqrt{W})$，其中 $N$ 是 A 的长度，$W = \max(A[i])$。

• 空间复杂度： $O(N)$。

统计信息

通过次数	提交次数	AC比率
3336	9251	36.1%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言