英文原文
You are given the root of a binary tree. We install cameras on the tree nodes where each camera at a node can monitor its parent, itself, and its immediate children.
Return the minimum number of cameras needed to monitor all nodes of the tree.
Example 1:

Input: root = [0,0,null,0,0] Output: 1 Explanation: One camera is enough to monitor all nodes if placed as shown.
Example 2:

Input: root = [0,0,null,0,null,0,null,null,0] Output: 2 Explanation: At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. Node.val == 0
中文题目
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
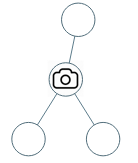
输入:[0,0,null,0,0] 输出:1 解释:如图所示,一台摄像头足以监控所有节点。
示例 2:
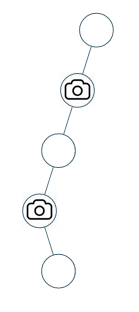
输入:[0,0,null,0,null,0,null,null,0] 输出:2 解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。
提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
通过代码
高赞题解
思路引入
这道题和「打家劫舍III」很像,一样是二叉树。装摄像头难道是防盗?
打家劫舍III 规定不能打劫相邻的节点,求打劫节点值的最大收益。对于每个节点,要么打劫,要么不打劫,描述一个子树的最大收益需要两个变量:它的根节点、是否打劫根节点。
思路
对于一个节点,它有什么状态,仅仅是放与不放相机吗?
还有:是否被监控到。
并且,被监控到的节点,也可以放相机。
需要三个变量去描述节点的状态:节点本身(代表不同子树)、是否放了相机、是否被监控。
定义递归函数 minCam,返回:以当前 root 为根节点的子树,需要放置的最少相机数。
当前子树的minCam = 左子树的minCam + 右子树的minCam + 1(不一定+1),位于底部的 base case 易得,自上而下地递归,答案自下而上地返回。
递归函数的参数,对应上述三个变量:
当前遍历的 root。
placeCam:root 处是否放相机。
watched:root 是否被父亲或自己监控。(因为递归是父亲调用儿子,对于当前节点,它只知道父亲和自己是否监控自己,不知道儿子是否监控自己)
分情况讨论
对于一个子树的根节点,它的状态无非下面三种,可以对应求出:不同状态下的子树 minCam。

当前节点 root 放了相机(当前子树的相机数保底为1)
左右儿子都没有放相机,都被父亲 root 监控
minCam(root.left, false, true) + minCam(root.right, false, true)左儿子放了相机,被自己监控。右儿子没有相机,被父亲 root 监控
minCam(root.left, true, true) + minCam(root.right, false, true)左儿子没有相机,被父亲 root 监控,右儿子放了相机,被自己监控
minCam(root.left, false, true) + minCam(root.right, true, true)
当前节点 root 没有相机,但被 root 的父亲监控
两个儿子都有相机,自己被自己监控
左儿子有相机,被自己监控,右儿子没有相机,被自己儿子监控
右儿子有相机,被自己监控,左儿子没有相机,被自己儿子监控
两个儿子都没有相机,被它们自己的儿子监控
当前节点 root 没有相机,也没有被父亲监控,是被儿子监控
两个儿子都有相机,自己被自己监控
左儿子有相机,被自己监控,右儿子没有相机,被自己儿子监控
左儿子没有相机,被自己儿子监控。右儿子有相机,被自己监控
递归的入口
整个树的根节点,它被监控,分两种情况:
根节点有相机。
根节点没有相机,没有父亲所以没有被父亲监控,但被儿子监控。
对这两种情况求 minCam,取结果较小者。
const minCameraCover = (root) => {
const minCam = (root, placeCam, watched) => {
// 省略
};
return Math.min(minCam(root, true, true), minCam(root, false, false));
};
递归的结束条件
即 base case。当遍历到 null 节点时:
if (root == null) {
if (placeCam) { // 父节点问当前null节点: 有相机的minCam,但null节点不可能有相机
return Infinity; // 返回无穷大,这个无穷大在取min时被忽略掉
} else { // 父节点问当前null节点: 没有相机的minCam,null没有子节点,下面没有相机
return 0; // 返回0
}
}
执行结果:对是对,遇到这个 case 就超时

代码 (超时)
const minCameraCover = (root) => {
// 以root为根节点的子树,放置的最少相机数
const minCam = (root, placeCam, watched) => {
if (root == null) { // 遍历到null节点
if (placeCam) { // 父节点问自己有相机的情况,但臣妾办不到
return Infinity; // 返回一个无穷大,让这个返回值失效
} else {
return 0;
}
}
if (placeCam) { // root放置相机
return 1 + Math.min( // root放了相机,相机数有 1 保底
minCam(root.left, false, true) + minCam(root.right, false, true),
minCam(root.left, true, true) + minCam(root.right, false, true),
minCam(root.left, false, true) + minCam(root.right, true, true)
);
} else {
if (watched) { // root没放相机,但被父亲监控了
return Math.min(
minCam(root.left, true, true) + minCam(root.right, true, true),
minCam(root.left, true, true) + minCam(root.right, false, false),
minCam(root.left, false, false) + minCam(root.right, true, true),
minCam(root.left, false, false) + minCam(root.right, false, false)
);
} else { // root没有相机,也没被父亲监控,被儿子监控了
return Math.min(
minCam(root.left, true, true) + minCam(root.right, true, true),
minCam(root.left, true, true) + minCam(root.right, false, false),
minCam(root.left, false, false) + minCam(root.right, true, true)
);
}
}
};
return Math.min(
minCam(root, true, true), // 根节点有相机
minCam(root, false, false) // 根节点没有相机,因为没有父亲,没有被父亲监控,是被儿子监控
);
};
怎么优化?
我们多次重复调用左右子树,传参很多是重复的。我们用了三次调用去求一个子树的三种状态下的 minCam。
现在放到一次调用里做,一次调用就求出当前子树的三种状态下的 minCam:
withCam :当前子树 root 有相机,情况下的 minCam
noCamWatchByDad :当前子树 root 没有相机,被父亲监控,情况下的minCam
noCamWatchBySon :当前子树 root 没有相机,被儿子监控,情况下的minCam
把这三个 minCam 返回给父调用,一次递归调用就返回出当前子树的三种状态:
return { withCam, noCamWatchByDad, noCamWatchBySon };
当前子树,通过子递归调用,拿到左右子树返回出的三种状态,去递推出当前子树的三种状态:withCam、noCamWatchByDad、noCamWatchBySon。
const left = minCam(root.left);
const right = minCam(root.right);
这样就是树形 DP,一次递归调用,只用执行两次子调用。
优化后代码
const minCameraCover = (root) => {
const minCam = (root) => {
if (root == null) { // base case
return {
withCam: Infinity,
noCamWatchByDad: 0,
noCamWatchBySon: 0
};
}
const left = minCam(root.left); // 左子树的minCam
const right = minCam(root.right); // 右子树的minCam
// 下面相当于状态转移方程
const withCam = 1 + Math.min(
left.noCamWatchByDad + right.noCamWatchByDad,
left.withCam + right.noCamWatchByDad,
left.noCamWatchByDad + right.withCam
);
const noCamWatchByDad = Math.min(
left.withCam + right.withCam,
left.withCam + right.noCamWatchBySon,
left.noCamWatchBySon + right.withCam,
left.noCamWatchBySon + right.noCamWatchBySon
);
const noCamWatchBySon = Math.min(
left.withCam + right.withCam,
left.withCam + right.noCamWatchBySon,
left.noCamWatchBySon + right.withCam
);
return { withCam, noCamWatchByDad, noCamWatchBySon };
};
const res = minCam(root); // 相当于dp[root]
return Math.min(res.withCam, res.noCamWatchBySon); // 相当于 min(dp[root][0],dp[root][2])
};
复盘总结
贪心算法我不熟,它有点像碰运气,有的行得通,有的行不通,不好用数学证明其正确性。
树形 DP 不像常规 DP 那样在迭代中 “填表”,而是在递归遍历中 “填表”。
没有开辟 DP 数组去存中间状态,而是通过子调用将状态返回出去,提供给父调用。
动态规划是根据过去的状态求出当前状态,按顺序一个个求。这里是沿着一棵树去求解子问题,可以理解为在一棵树上填表。
可以理解为,递归调用栈把中间计算结果暂存了,子调用的结果交给父调用,它就销毁了,并没有记忆化。
当然,你也可以开辟容器,key 是节点(子树),value 是子树的计算结果。
但没有必要,因为中间计算结果不需要存储,所以这算是降维优化了。
随着递归的出栈,子调用不断向上返回,子问题(子树)被一个个解决。最后求出大问题:整个树的最小相机数。
感谢阅读,点赞更棒。真诚地在写,话也是我想说的,相信你也感受的到。尽量在用短句,保证易读和流畅性。欢迎具体建议和反馈。
最后修改于:2021-10-15
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 26687 | 53304 | 50.1% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|
相似题目
| 题目 | 难度 |
|---|---|
| 在二叉树中分配硬币 | 中等 |




