原文链接: https://leetcode-cn.com/problems/er-cha-shu-ren-wu-diao-du

英文原文

中文题目

任务调度优化是计算机性能优化的关键任务之一。在任务众多时，不同的调度策略可能会得到不同的总体执行时间，因此寻求一个最优的调度方案是非常有必要的。

通常任务之间是存在依赖关系的，即对于某个任务，你需要先完成他的前导任务（如果非空），才能开始执行该任务。我们保证任务的依赖关系是一棵二叉树，其中 root 为根任务，root.left 和 root.right 为他的两个前导任务（可能为空），root.val 为其自身的执行时间。

在一个 CPU 核执行某个任务时，我们可以在任何时刻暂停当前任务的执行，并保留当前执行进度。在下次继续执行该任务时，会从之前停留的进度开始继续执行。暂停的时间可以不是整数。

现在，系统有两个 CPU 核，即我们可以同时执行两个任务，但是同一个任务不能同时在两个核上执行。给定这颗任务树，请求出所有任务执行完毕的最小时间。

示例 1：

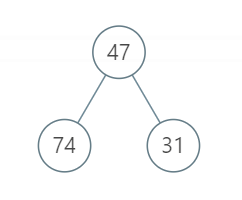
输入：root = [47, 74, 31]

输出：121

解释：根节点的左右节点可以并行执行31分钟，剩下的43+47分钟只能串行执行，因此总体执行时间是121分钟。

示例 2：

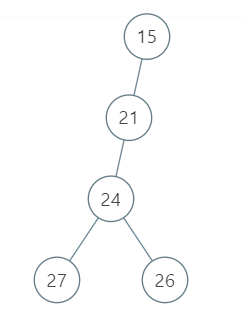
输入：root = [15, 21, null, 24, null, 27, 26]

输出：87

示例 3：

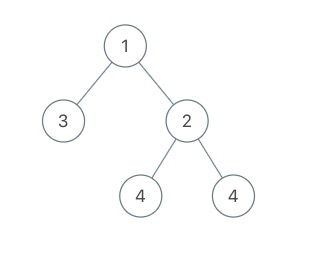
输入：root = [1,3,2,null,null,4,4]

输出：7.5

限制：

• 1 <= 节点数量 <= 1000
• 1 <= 单节点执行时间 <= 1000

通过代码

高赞题解

我们设 $f(i)$ 为节点 $i$ 的最短时间，然后分类讨论。

如果 $i$ 是一个叶子，那么显然 $f(i) = val(i)$。如果 $i$ 只有一个儿子，那么先要执行完儿子才轮得到自己，$f(i) = f(son(i)) + val(i)$。

如果 $i$ 有两个儿子 $l, r$，那么我们就可以考虑用双核来优化。一种最简单的优化策略是：两个子树分别使用双核跑完，然后再根节点跑。这样的时间消耗是 $f(l)+f(r) + val(i)$。

还有一种策略是：在左边花费 $x$ 时间使用双核（这里是有效使用，即两个核都必须用上，后同），在右边花费 $y$ 时间使用双核，然后在左右两棵子树一边一个核。可以看出，第三个样例使用的正是这样的策略，在根节点的右子树先花费了 3.5 的时间，然后左右两边一边一个核花费 3 时间。

那么，这种情况下，设左右子树的任务总时间和分别为 $sum(l), sum(r)$。则通过利用双核，左子树剩下的任务时间变成了 $sum(l) - 2x$，右子树剩下的任务时间变成了 $sum(r) - 2y$，然后一边一个核处理完剩下的任务所需时间为这两者的较大者。因而总时间为
$$
val(i) + x+y+\max\left\lbrace sum(l) - 2x , sum(r) - 2y \right\rbrace
$$
即
$$
val(i) + \max\left\lbrace sum(l) +y-x , sum(r) -(y-x)\right\rbrace
$$

$val(i)$ 的时间消耗是逃不掉的，我们考虑后面这个 $\max$ 怎样取得尽量小。设 $t=y-x$，那么后面这个 $\max$ 要取到最小当且仅当 $t^* = mid = \frac{sum(r) - sum(l)}{2}$。并且如果 $t$ 偏离 $mid$ 越远，那么这个 $\max$ 就越大。注意到 $x \in [0, sum(l) - f(l)], y \in [0, sum(r) - f(r)]$，就有 $t\in [f(l) - sum(l), sum(r) - f(r)]$。通过对 $mid$ 和这个区间位置的讨论，我们就能算出这个 $\max$ 的最小值。

最后把以上这些情况统合起来，就有下面的转移方程：
$$
f(i) = val(i) + \min\left\lbrace f(l)+ f(r), \min_{t\in [f(l) - sum(l), sum(r) - f(r)]}\max\left\lbrace sum(l) +t , sum(r) -t\right\rbrace \right\rbrace
$$
其中规定如果 $l$ 或者 $r$ 为空，对应的 $sum, f$ 均为 $0$。

时间复杂度 $O(n)$。

class Solution:
    def minimalExecTime(self, root: TreeNode) -> float:
        def dfs(cur):
            if cur == None:
                return 0, 0
            fl, sml = dfs(cur.left)
            fr, smr = dfs(cur.right)
            f, sm = cur.val + fl + fr, cur.val + sml + smr
            gl, gr = sml - fl, smr - fr
            mid = (cur.right.sm - cur.left.sm) / 2
            t = -gl if mid < -gl else (gr if mid > gr else mid)
            f = min(f, cur.val + max(sml + t, smr - t))
            return f, sm

        ans, _ = dfs(root)
        return ans

统计信息

通过次数	提交次数	AC比率
1901	3194	59.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言