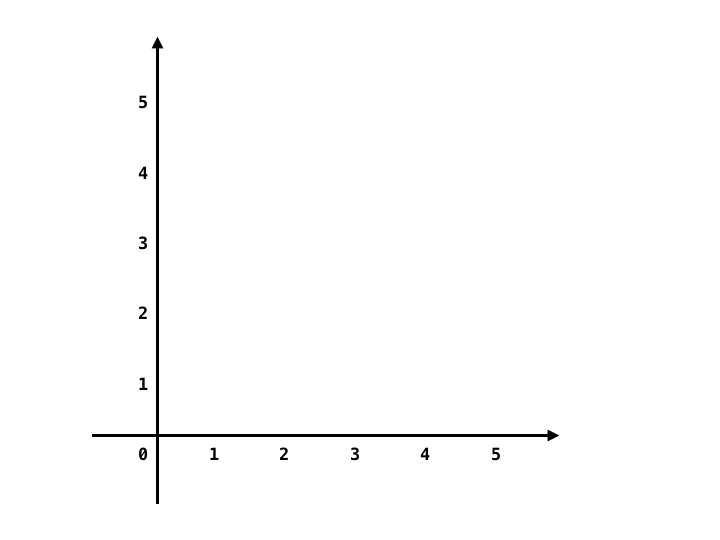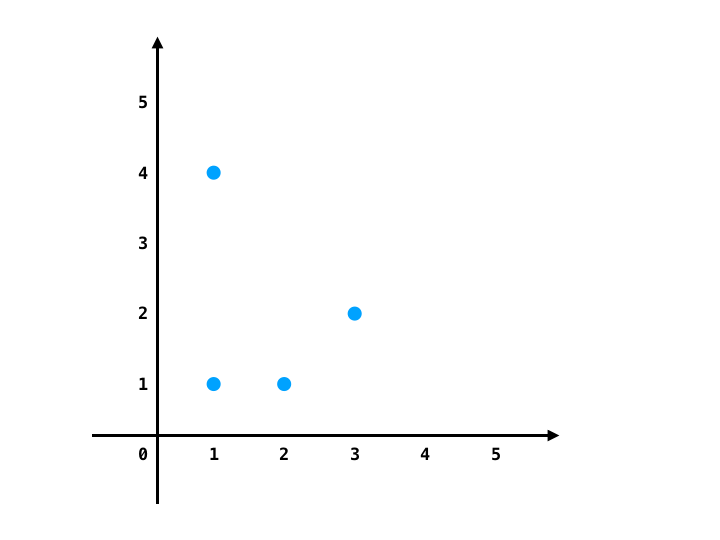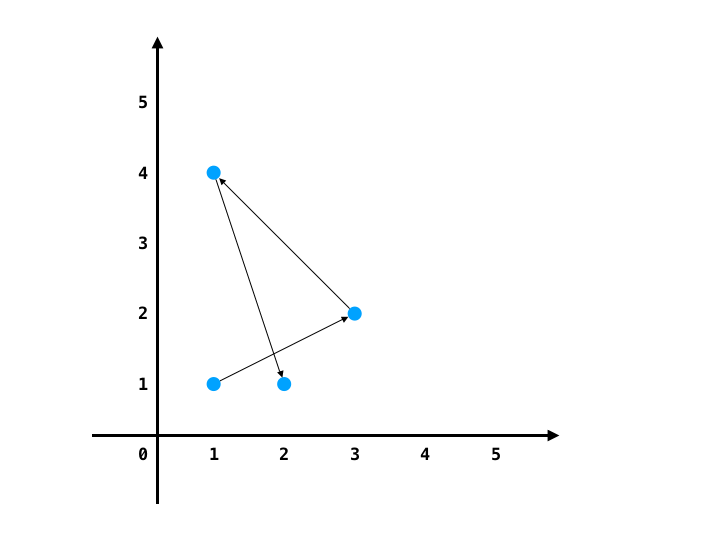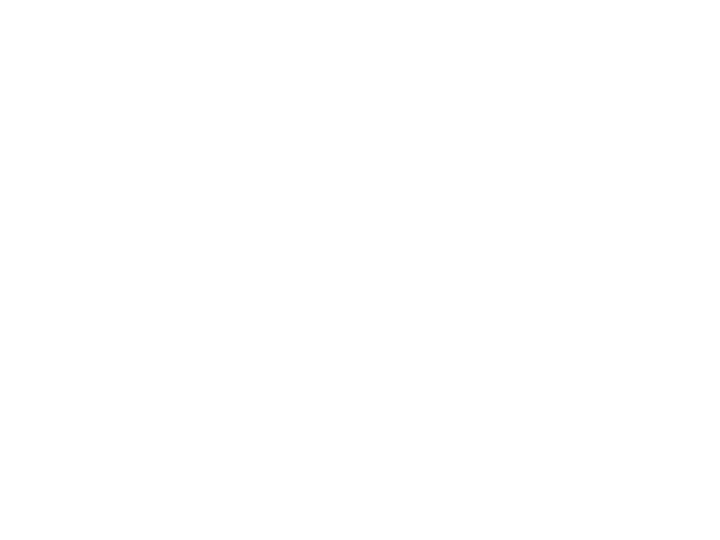原文链接: https://leetcode-cn.com/problems/you-le-yuan-de-mi-gong

英文原文

中文题目

小王来到了游乐园，她玩的第一个项目是模拟推销员。有一个二维平面地图，其中散布着 N 个推销点，编号 0 到 N-1，不存在三点共线的情况。每两点之间有一条直线相连。游戏没有规定起点和终点，但限定了每次转角的方向。首先，小王需要先选择两个点分别作为起点和终点，然后从起点开始访问剩余 N-2 个点恰好一次并回到终点。访问的顺序需要满足一串给定的长度为 N-2 由 L 和 R 组成的字符串 direction，表示从起点出发之后在每个顶点上转角的方向。根据这个提示，小王希望你能够帮她找到一个可行的遍历顺序，输出顺序下标（若有多个方案，输出任意一种）。可以证明这样的遍历顺序一定是存在的。

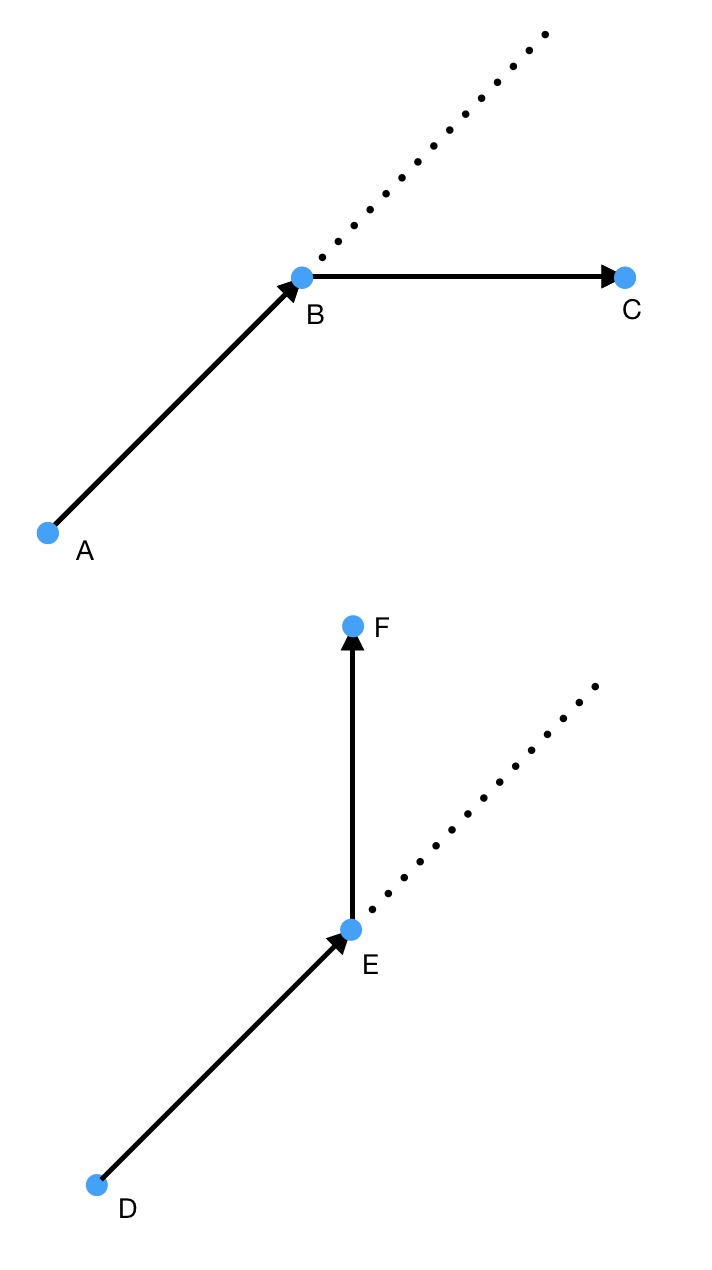
（上图：A->B->C 右转； 下图：D->E->F 左转）

示例 1：

输入：points = [[1,1],[1,4],[3,2],[2,1]], direction = "LL"

输入：[0,2,1,3]

解释：[0,2,1,3] 是符合"LL"的方案之一。在 [0,2,1,3] 方案中，0->2->1 是左转方向， 2->1->3 也是左转方向

示例 2：

输入：points = [[1,3],[2,4],[3,3],[2,1]], direction = "LR"

输入：[0,3,1,2]

解释：[0,3,1,2] 是符合"LR"的方案之一。在 [0,3,1,2] 方案中，0->3->1 是左转方向， 3->1->2 是右转方向

限制：

• 3 <= points.length <= 1000 且 points[i].length == 2
• 1 <= points[i][0],points[i][1] <= 10000
• direction.length == points.length - 2
• direction 只包含 "L","R"

通过代码

高赞题解

构造方法:

1. 选取一个凸包顶点作为起点.
2. 如果下一步要左(右)拐,移动到逆(顺)时针凸包上下一个顶点.
   
   如图,如果沿着红色箭头移动到逆时针下一个点,那么下一步(绿色箭头)无论走向哪个点,都是左拐.
3. 去掉当前点并移动到下一个点时,下一个点仍在新的凸包上,因此可以回到第2步.

1’. 因为没有三点共线,横(纵)坐标最小(大)的点一定在凸包上,随便选一个即可.
2’. 如何找到逆(顺)时针方向凸包上下一个顶点?
使用叉积,以逆时针为例,如果$B$是$A$逆时针方向下一个点,那么对于所有其他点$C$都有:
$$\vec{AB}\times\vec{AC}>0.$$

复杂度为$O(n^2)$.代码中$m$为当前点,$q$为下一个点.

using LL = long long;
struct Point{
    LL x, y;
    Point operator - (const Point& p){
        return{x - p.x, y - p.y};
    }
    LL operator * (const Point &p){
        return x * p.y - y * p.x;
    }
};
class Solution {
public:
    
    vector<int> visitOrder(vector<vector<int>>& points, string direction) {
        int n = points.size();
        vector<int> ans;
        vector<int> vis(n);
        vector<Point> vp(n);
        for(int i = 0; i < n; i += 1) vp[i] = {points[i][0], points[i][1]};
        int m = 0;
        for(int i = 1; i < n; i += 1)
            if(vp[i].x < vp[m].x) m = i;
        ans.push_back(m);
        vis[m] = 1;
        for(int i = 0; i < n - 2; i += 1){
            int q = -1;
            for(int j = 0; j < n; j += 1) if(not vis[j])
                if(q == -1) q = j;
                else{
                    if(direction[i] == 'L'){
                        if((vp[q] - vp[m]) * (vp[j] - vp[m]) < 0) q = j;
                    }
                    else{
                        if((vp[q] - vp[m]) * (vp[j] - vp[m]) > 0) q = j;
                    }
                }
            m = q;
            vis[q] = 1;
            ans.push_back(m);
        }
        for(int i = 0; i < n; i += 1) if(not vis[i]) ans.push_back(i);
        return ans;
    }
};

统计信息

通过次数	提交次数	AC比率
909	1567	58.0%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言