原文链接: https://leetcode-cn.com/problems/DFPeFJ

英文原文

中文题目

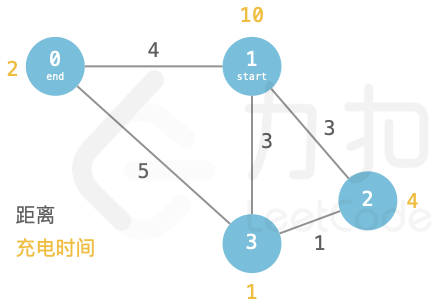
小明的电动车电量充满时可行驶距离为 `cnt`，每行驶 1 单位距离消耗 1 单位电量，且花费 1 单位时间。小明想选择电动车作为代步工具。地图上共有 N 个景点，景点编号为 0 ~ N-1。他将地图信息以 `[城市 A 编号,城市 B 编号,两城市间距离]` 格式整理在在二维数组 `paths`，表示城市 A、B 间存在双向通路。初始状态，电动车电量为 0。每个城市都设有充电桩，`charge[i]` 表示第 i 个城市每充 1 单位电量需要花费的单位时间。请返回小明最少需要花费多少单位时间从起点城市 `start` 抵达终点城市 `end`。

示例 1：

输入：paths = [[1,3,3],[3,2,1],[2,1,3],[0,1,4],[3,0,5]], cnt = 6, start = 1, end = 0, charge = [2,10,4,1]

输出：43

解释：最佳路线为：1->3->0。
在城市 1 仅充 3 单位电至城市 3，然后在城市 3 充 5 单位电，行驶至城市 5。
充电用时共 3*10 + 5*1= 35
行驶用时 3 + 5 = 8，此时总用时最短 43。

示例 2：

输入：paths = [[0,4,2],[4,3,5],[3,0,5],[0,1,5],[3,2,4],[1,2,8]], cnt = 8, start = 0, end = 2, charge = [4,1,1,3,2]

输出：38

解释：最佳路线为：0->4->3->2。
城市 0 充电 2 单位，行驶至城市 4 充电 8 单位，行驶至城市 3 充电 1 单位，最终行驶至城市 2。
充电用时 4*2+2*8+3*1 = 27
行驶用时 2+5+4 = 11，总用时最短 38。

提示：

• 1 <= paths.length <= 200
• paths[i].length == 3
• 2 <= charge.length == n <= 100
• 0 <= path[i][0],path[i][1],start,end < n
• 1 <= cnt <= 100
• 1 <= path[i][2] <= cnt
• 1 <= charge[i] <= 100
• 题目保证所有城市相互可以到达

通过代码

高赞题解

解题思路

我们将(city,charge)二元组视为节点，然后建图，以(start,0)为起点跑一遍Dijkstra即可得到结果。

新图的节点数为$\mathcal{O}(NC)$，边数为$\mathcal{O}(N(C+M))$。$C$为最大电量，$M$为原来的边数。

代码

const int INF = 0x3f3f3f3f;

class Solution {
public:
    int electricCarPlan(vector<vector<int>>& paths, int cnt, int start, int end, vector<int>& charge) {
        int n = charge.size();
        vector<vector<int>> dist(n, vector<int>(cnt + 1, INF));
        dist[start][0] = 0;
        
        vector<vector<pair<int, int>>> adj(n);
        for (auto &path : paths) {
            int u = path[0], v = path[1], w = path[2];
            adj[u].emplace_back(v, w);
            adj[v].emplace_back(u, w);
        }
        priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<>> pq;
        pq.emplace(0, start, 0);
        
        while (!pq.empty()) {
            auto [t, u, c] = pq.top();
            pq.pop();
            if (t > dist[u][c])
                continue;
            if (u == end)
                return t;

            // 当前电不满，充电一分钟，状态变为(u,c+1)
            if (c < cnt) {
                int nt = t + charge[u];
                if (nt < dist[u][c + 1]) {
                    dist[u][c + 1] = nt;
                    pq.emplace(nt, u, c + 1);
                }
            }

            // 如果一条边(u,v,w)能走，尝试走这条边，状态变为(v,c-w)
            for (auto [v, w] : adj[u]) {
                if (c >= w && t + w < dist[v][c - w]) {
                    dist[v][c - w] = t + w;
                    pq.emplace(t + w, v, c - w);
                }
            }
        }
        
        return -1;
    }
};

统计信息

通过次数	提交次数	AC比率
1260	3101	40.6%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言