原文链接: https://leetcode-cn.com/problems/vFjcfV

英文原文

中文题目

「力扣挑战赛」场地外，小力组织了一个套玩具的游戏。所有的玩具摆在平地上，`toys[i]` 以 `[xi,yi,ri]` 的形式记录了第 `i` 个玩具的坐标 `(xi,yi)` 和半径 `ri`。小扣试玩了一下，他扔了若干个半径均为 `r` 的圈，`circles[j]` 记录了第 `j` 个圈的坐标 `(xj,yj)`。套圈的规则如下： - 若一个玩具被某个圈完整覆盖了（即玩具的任意部分均在圈内或者圈上），则该玩具被套中。 - 若一个玩具被多个圈同时套中，最终仅计算为套中一个玩具

请帮助小扣计算，他成功套中了多少玩具。

注意：

• 输入数据保证任意两个玩具的圆心不会重合，但玩具之间可能存在重叠。

示例 1：

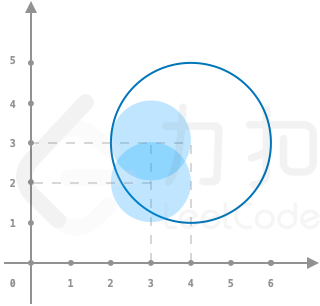
输入：toys = [[3,3,1],[3,2,1]], circles = [[4,3]], r = 2

输出：1

解释： 如图所示，仅套中一个玩具

示例 2：

输入：toys = [[1,3,2],[4,3,1],[7,1,2]], circles = [[1,0],[3,3]], r = 4

输出：2

解释： 如图所示，套中两个玩具
{:width=”400px”}

提示：

• 1 <= toys.length <= 10^4
• 0 <= toys[i][0], toys[i][1] <= 10^9
• 1 <= circles.length <= 10^4
• 0 <= circles[i][0], circles[i][1] <= 10^9
• 1 <= toys[i][2], r <= 10

通过代码

高赞题解

注意到半径很小，我们可以枚举每个玩具，并暴力枚举该玩具周围是否有可以套住该玩具的圈。

具体来说，将 $\textit{circles}$ 排序后，将横坐标相同的圈分为一组。对每个玩具，可以套住该玩具的圈，在横坐标上，必然满足圈的最右端点不小于玩具的最右端点，且圈的最左端点不大于玩具的最左端点。对于纵坐标，我们只需要找最接近玩具纵坐标的上下两个圈。这样我们就可以二分出圈的横坐标的范围，对每个横坐标上的圈二分纵坐标最接近玩具纵坐标的圈。

func circleGame(toys [][]int, circles [][]int, r0 int) (ans int) {
	sort.Slice(circles, func(i, j int) bool { a, b := circles[i], circles[j]; return a[0] < b[0] || a[0] == b[0] && a[1] < b[1] })

	// 将横坐标相同的圈分为一组
	type pair struct{ x int; ys []int }
	a, y := []pair{}, -1
	for _, p := range circles {
		if len(a) == 0 || p[0] > a[len(a)-1].x {
			a = append(a, pair{p[0], []int{p[1]}})
			y = -1
		} else if p[1] > y { // 去重
			a[len(a)-1].ys = append(a[len(a)-1].ys, p[1])
			y = p[1]
		}
	}

	for _, t := range toys {
		x, y, r := t[0], t[1], t[2]
		if r > r0 {
			continue
		}
		i := sort.Search(len(a), func(i int) bool { return a[i].x+r0 >= x+r })
		for ; i < len(a) && a[i].x-r0 <= x-r; i++ {
			cx, ys := a[i].x, a[i].ys
			j := sort.SearchInts(ys, y)
			if j < len(ys) {
				if cy := ys[j]; (x-cx)*(x-cx)+(y-cy)*(y-cy) <= (r0-r)*(r0-r) {
					ans++
					break
				}
			}
			if j > 0 {
				if cy := ys[j-1]; (x-cx)*(x-cx)+(y-cy)*(y-cy) <= (r0-r)*(r0-r) {
					ans++
					break
				}
			}
		}
	}
	return
}

统计信息

通过次数	提交次数	AC比率
1098	5356	20.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言