英文原文
You are given two integer arrays nums1 and nums2. We write the integers of nums1 and nums2 (in the order they are given) on two separate horizontal lines.
We may draw connecting lines: a straight line connecting two numbers nums1[i] and nums2[j] such that:
nums1[i] == nums2[j], and- the line we draw does not intersect any other connecting (non-horizontal) line.
Note that a connecting line cannot intersect even at the endpoints (i.e., each number can only belong to one connecting line).
Return the maximum number of connecting lines we can draw in this way.
Example 1:
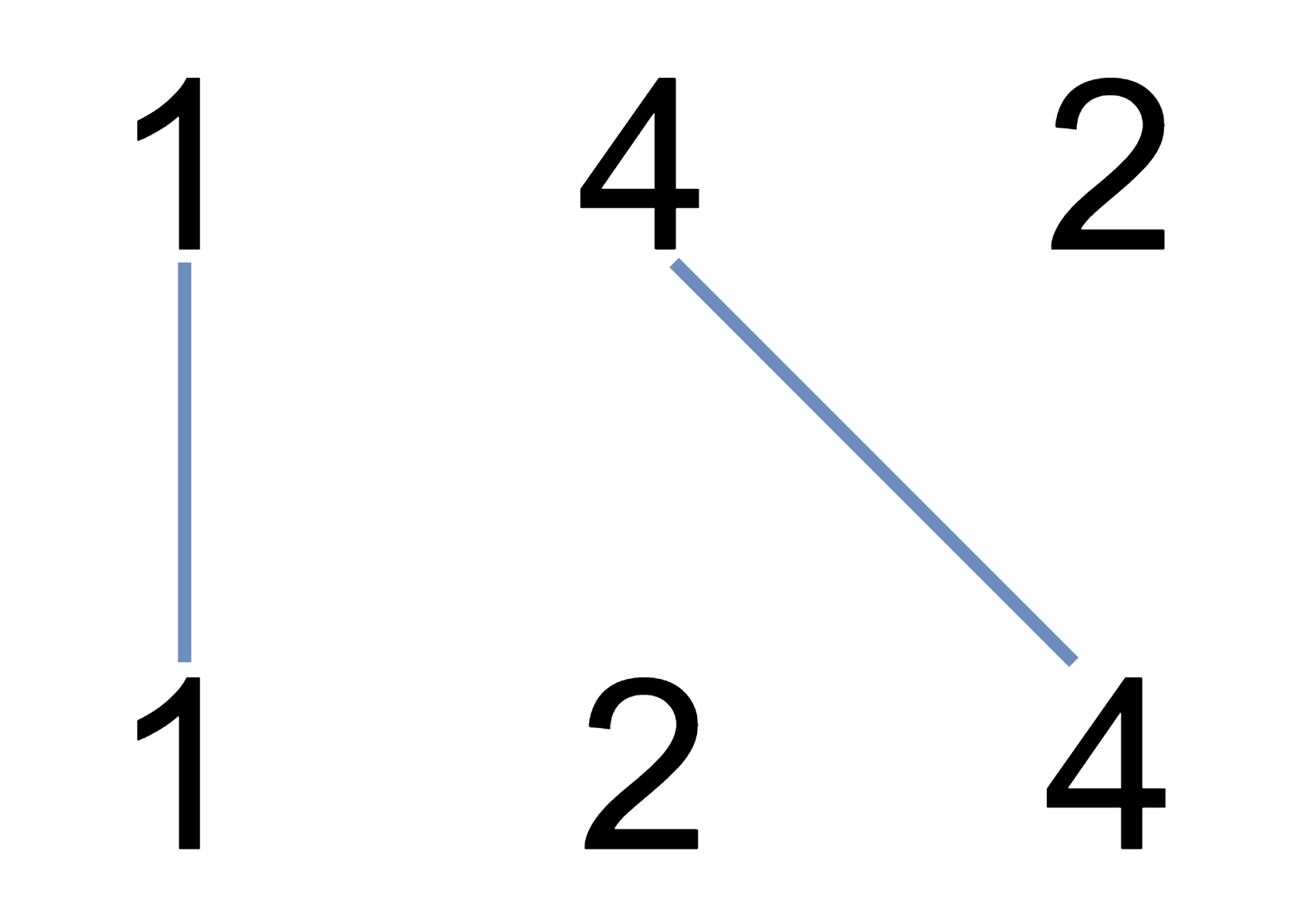
Input: nums1 = [1,4,2], nums2 = [1,2,4] Output: 2 Explanation: We can draw 2 uncrossed lines as in the diagram. We cannot draw 3 uncrossed lines, because the line from nums1[1] = 4 to nums2[2] = 4 will intersect the line from nums1[2]=2 to nums2[1]=2.
Example 2:
Input: nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2] Output: 3
Example 3:
Input: nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1] Output: 2
Constraints:
1 <= nums1.length, nums2.length <= 5001 <= nums1[i], nums2[j] <= 2000
中文题目
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足满足:
-
nums1[i] == nums2[j] - 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例 1:

输入:nums1 = [1,4,2], nums2 = [1,2,4] 输出:2 解释:可以画出两条不交叉的线,如上图所示。 但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。
示例 2:
输入:nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2] 输出:3
示例 3:
输入:nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1] 输出:2
提示:
1 <= nums1.length, nums2.length <= 5001 <= nums1[i], nums2[j] <= 2000
通过代码
高赞题解
动态规划
这是一道「最长公共子序列(LCS)」的轻度变形题。
为了让你更好的与「最长公共子序列(LCS)」裸题进行对比,我们使用 $s1$ 代指 $nums1$,$s2$ 代指 $nums2$。
对于这类题都使用如下「状态定义」即可:
$f[i][j]$ 代表考虑 $s1$ 的前 $i$ 个字符、考虑 $s2$ 的前 $j$ 的字符,形成的最长公共子序列长度。
然后不失一般性的考虑 $f[i][j]$ 如何转移。
由于我们的「状态定义」只是说「考虑前 $i$ 个和考虑前 $j$ 个字符」,并没有说「一定要包含第 $i$ 个或者第 $j$ 个字符」(这也是「最长公共子序列 LCS」与「最长上升子序列 LIS」状态定义上的最大不同)。
我们需要考虑「不包含 $s1[i]$,不包含 $s2[j]$」、「不包含 $s1[i]$,包含 $s2[j]$」「包含 $s1[i]$,不包含 $s2[j]$」、「包含 $s1[i]$,包含 $s2[j]$」四种情况:
- 不包含 $s1[i]$,不包含 $s2[j]$:结合状态定义,可以使用 $f[i - 1][j - 1]$ 进行精确表示。
- 包含 $s1[i]$,包含 $s2[j]$:前提是 $s1[i] = s2[j]$,可以使用 $f[i - 1][j - 1] + 1$ 进行精确表示。
- 不包含 $s1[i]$,包含 $s2[j]$:结合状态定义,我们无法直接将该情况表示出来。
注意 $f[i - 1][j]$ 只是表示「必然不包含 $s1[i]$,但可能包含$s2[j]$」的情况,也就是说 $f[i - 1][j]$ 其实是该情况与情况 $1$ 的合集。
但是由于我们求的是「最大值」,只需要确保「不漏」即可保证答案的正确(某些情况被重复参与比较不影响正确性),因此这里直接使用 $f[i - 1][j]$ 进行表示没有问题。 - 包含 $s1[i]$,不包含 $s2[j]$:与情况 $3$ 同理,直接使用 $f[i][j - 1]$ 表示没有问题。
$f[i][j]$ 就是在上述所有情况中取 $max$ 而来,由于情况 $1$ 被 情况 $3$ 和 情况 $4$ 所包含,因此我们只需要考虑 $f[i - 1][j]$、$f[i][j -1]$ 和 $f[i - 1][j - 1] + 1$ 三种状态即可,其中最后一种状态需要满足 $s1[i] = s2[j]$ 前提条件。
因此我们最后的状态转移方程为:
$$
f[i][j]=\begin{cases}
\max(f[i - 1][j], f[i][j - 1], f[i - 1][j - 1] + 1) & s1[i] = s2[j] \
\max(f[i - 1][j], f[i][j - 1]) & s1[i] \neq s2[j] \
\end{cases}
$$
上述分析过程建议加深理解,估计很多同学能 AC 但其实并不知道 LCS 问题的状态转移是包含了「重复状态比较」的。
代码:
[]class Solution { public int maxUncrossedLines(int[] s1, int[] s2) { int n = s1.length, m = s2.length; int[][] f = new int[n + 1][m + 1]; for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { f[i][j] = Math.max(f[i - 1][j], f[i][j - 1]); if (s1[i - 1] == s2[j - 1]) { f[i][j] = Math.max(f[i][j], f[i - 1][j - 1] + 1); } } } return f[n][m]; } }
- 时间复杂度:$O(n * m)$
- 空间复杂度:$O(n * m)$
最后
如果有帮助到你,请给题解点个赞和收藏,让更多的人看到 ~ (“▔□▔)/
也欢迎你 关注我 和 加入我们的「组队打卡」小群 ,提供写「证明」&「思路」的高质量题解
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 37396 | 58662 | 63.7% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|
相似题目
| 题目 | 难度 |
|---|---|
| 编辑距离 | 困难 |




