原文链接: https://leetcode-cn.com/problems/path-in-zigzag-labelled-binary-tree

英文原文

In an infinite binary tree where every node has two children, the nodes are labelled in row order.

In the odd numbered rows (ie., the first, third, fifth,...), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,...), the labelling is right to left.

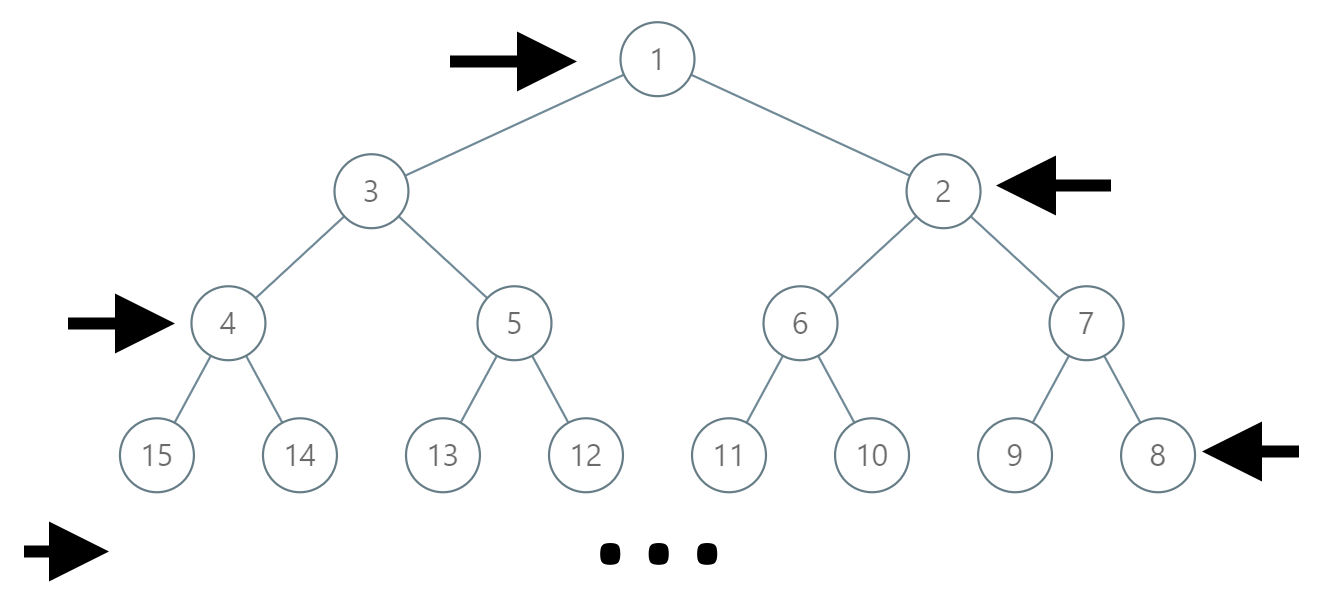
Given the label of a node in this tree, return the labels in the path from the root of the tree to the node with that label.

 

Example 1:

Input: label = 14
Output: [1,3,4,14]

Example 2:

Input: label = 26
Output: [1,2,6,10,26]

 

Constraints:

• 1 <= label <= 10^6

中文题目

在一棵无限的二叉树上，每个节点都有两个子节点，树中的节点 逐行 依次按 “之” 字形进行标记。

如下图所示，在奇数行（即，第一行、第三行、第五行……）中，按从左到右的顺序进行标记；

而偶数行（即，第二行、第四行、第六行……）中，按从右到左的顺序进行标记。

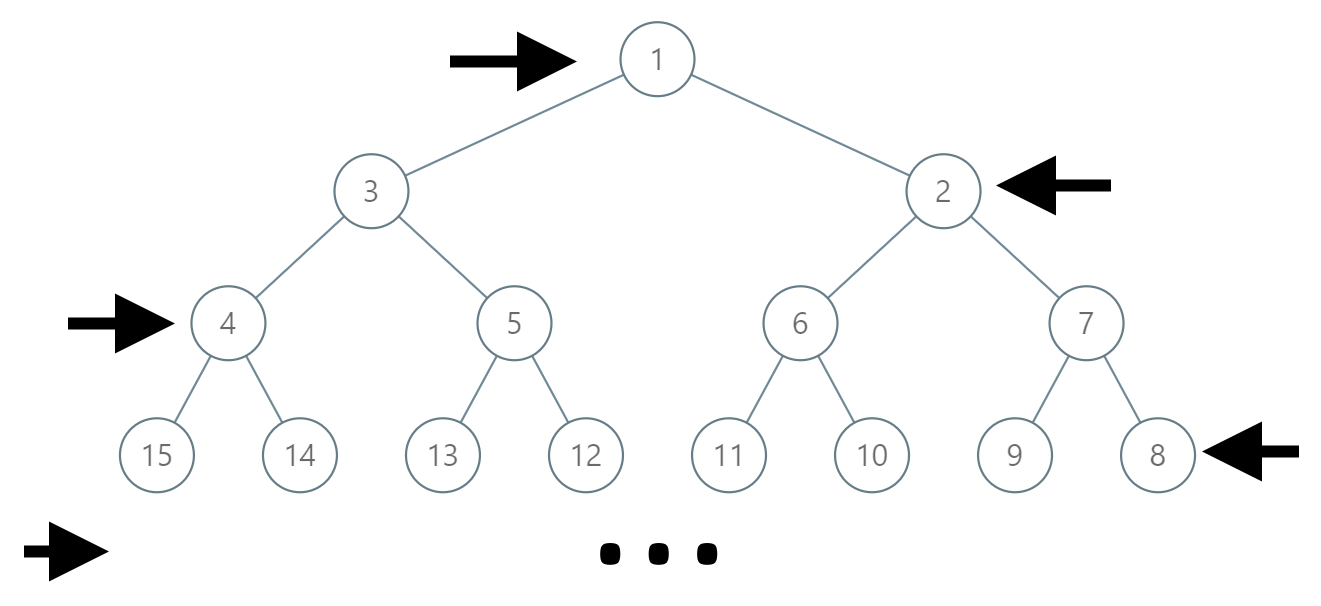
给你树上某一个节点的标号 label，请你返回从根节点到该标号为 label 节点的路径，该路径是由途经的节点标号所组成的。

 

示例 1：

输入：label = 14
输出：[1,3,4,14]

示例 2：

输入：label = 26
输出：[1,2,6,10,26]

 

提示：

• 1 <= label <= 10^6

通过代码

高赞题解

思路：

我们先不考虑题目中特殊化的二叉树，先思考如何恢复正常的二叉树的路径

补充知识：
若已知一节点为 $i$，则该节点的左孩子节点为 $(2 * i)$，右孩子节点为 $(2 * i + 1)$
且该节点的父节点为 $(i ,/, 2)$

对于正常的二叉树，已知节点 $i$，根据上述知识我们便可以求得其路径：

vector <int> ans;
while(label) {
    ans.push_back(label);
    label >>= 1;
}

当 $label = 14$，则 $ans =$ {$14, 7, 3, 1$}

之后我们需要将 $ans$ 转化为题目要求的二叉树的路径

令 $deep$ 为深度

观察题目要求的二叉树，其实不难发现：$deep$ 为偶数时和正常的二叉树是对称的，所以我们只需要对 $deep$ 为偶数时进行处理即可

那么我们如何将正常的数转化为我们需要的呢？

补充知识：
二叉树中第 $i$ 层一共有 $2 ^ {(i-1)}$ 个数，且前 $i - 1$ 层共有 $2 ^ {(i-1)} - 1$ 个数
注意： 这里的 $i$ 从 $1$ 开始，而在代码实现中 $i$ 从 $0$ 开始

为了和代码一致，下面的推导我们以 $i = 0$ 为第一层

以节点 $10$ 举例，假设节点 $10$ 的深度为 $i$，节点 $10$ 对应的是节点 $13$，首先我们需要第 $i$ 层的节点个数以及第 $i$ 层的第一个节点的编号 $l$ 和最后一个节点的编号 $r$

其实不难发现：

$$
l = 2^i\
r = 2 * l - 1\
13 = r - 10 + l
$$

由此我们可以根据节点 $10$ 求得节点 $13$

最后需要注意的是：要对 $ans$ 进行反转

代码实现：

class Solution {
public:
    vector<int> pathInZigZagTree(int label) {
        vector <int> ans;
        while(label) {
            ans.push_back(label);
            label >>= 1;
        }
        reverse(ans.begin(), ans.end());
        int l, r, deep = ans.size();
        for(int i = 0; i < deep; i++) {
            if((deep & 1) != (i & 1)) continue;     // 判断第 i 层是否需要修改
            l = (1 << i);
            r = l + l - 1;
            ans[i] = r - ans[i] + l;
        }
        return ans;
    }
};

具体解释一下代码中的 $(deep; &; 1)$ $!=$ $(i; &; 1)$

• 当 $deep$ 为 偶数 时，只对 奇数深度 进行修改
• 当 $deep$ 为 奇数 时，只对 偶数深度 进行修改

而 $deep$ 为二叉树的总深度，$i$ 为当前遍历的深度，我们可以通过 $deep; &; 1$ 可以判断 $deep$ 的奇偶
如果 $(deep; &; 1)$ $!=$ $(i; &; 1)$ 说明 $deep$ 和 $i$ 具有不同的奇偶性，此时需要对第 $i$ 层进行修改，但由于 $i = 0$ 为第一层，所以此时需要将 $i$ 理解为 $i + 1$ 才是当前真实的深度，故当 $(deep; &; 1)$ $!=$ $(i; &; 1)$ 时不需要修改

复杂度分析

• 时间复杂度：$O(\log label)$，求二叉树层数需 $O(\log label)$，$ans.size() = \log label$，则反转一次 $ans$ 需 $O(\log label)$，遍历一次 $ans$ 需 $O(\log label)$，总体为 $O(\log label)$

• 空间复杂度：$O(1)$，除返回需要的 $ans$ 外，额外需要的空间为 $O(1)$

运行结果：

统计信息

通过次数	提交次数	AC比率
29039	38173	76.1%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言