原文链接: https://leetcode-cn.com/problems/minimum-cost-tree-from-leaf-values
英文原文
Given an array arr of positive integers, consider all binary trees such that:
- Each node has either
0or2children; - The values of
arrcorrespond to the values of each leaf in an in-order traversal of the tree. - The value of each non-leaf node is equal to the product of the largest leaf value in its left and right subtree, respectively.
Among all possible binary trees considered, return the smallest possible sum of the values of each non-leaf node. It is guaranteed this sum fits into a 32-bit integer.
A node is a leaf if and only if it has zero children.
Example 1:
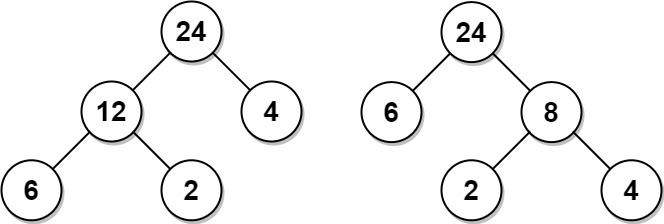
Input: arr = [6,2,4] Output: 32 Explanation: There are two possible trees shown. The first has a non-leaf node sum 36, and the second has non-leaf node sum 32.
Example 2:
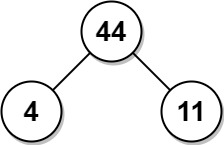
Input: arr = [4,11] Output: 44
Constraints:
2 <= arr.length <= 401 <= arr[i] <= 15- It is guaranteed that the answer fits into a 32-bit signed integer (i.e., it is less than 231).
中文题目
给你一个正整数数组 arr,考虑所有满足以下条件的二叉树:
- 每个节点都有 0 个或是 2 个子节点。
- 数组
arr中的值与树的中序遍历中每个叶节点的值一一对应。(知识回顾:如果一个节点有 0 个子节点,那么该节点为叶节点。) - 每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。
在所有这样的二叉树中,返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。
示例:
输入:arr = [6,2,4]
输出:32
解释:
有两种可能的树,第一种的非叶节点的总和为 36,第二种非叶节点的总和为 32。
24 24
/ \ / \
12 4 6 8
/ \ / \
6 2 2 4
提示:
2 <= arr.length <= 401 <= arr[i] <= 15- 答案保证是一个 32 位带符号整数,即小于
2^31。
通过代码
高赞题解
解题思路
首先,想让 mct 值最小,那么值较小的叶子节点就要尽量放到底部,值较大的叶子节点要尽量放到靠上的部分。因为越是底部的叶子节点,被用来做乘法的次数越多。这就决定了我们有必要去寻找一个极小值。通过维护一个单调递减栈就可以找到一个极小值,因为既然是单调递减栈,左侧节点一定大于栈顶节点,而当前节点(右侧)也大于栈顶节点(因为当前节点小于栈顶的话,就被直接入栈了)。
然后找到这个极小值后,就需要左右看看,左边和右边哪个值更小,因为我们的目的是把较小的值尽量放到底部。还有一点,构造出来的二叉树一定是形如下面图一的样子,比如 [6,2,3,4] 构成的二叉树:
图一 (最小 mct 一定形如以下的样子):
mct: 24 + 12 + 6 = 42
24
/ \
6 12
/ \
6 4
/ \
2 3图二 (这个容易想到,但是一定不是最小 mct):
mct: 24 + 12 + 12 = 48
24
/ \
12 12
/ \ / \
6 2 3 4在栈 st 的栈底,我们可以放一个 Integer.MAX_VALUE,方便做比较,分析一遍 [6,2,3,4] 的运行过程:
[Integer.MAX_VALUE], 6=> 入栈[Integer.MAX_VALUE, 6], 2=> 入栈[Integer.MAX_VALUE, 6, 2], 3=> 先取出 2,与 3 组合(左 6 右 3 中取较小的一个),然后把 3 入栈(3 会作为一侧最大值,参与后续乘法):
mct += st.pop() * Math.min(st.peek(), arr[i]);6 / \ 2 3[Integer.MAX_VALUE, 6, 3], 4=> 3,出栈,4 入栈,最终结果 mct 会加上 3 * 4 的值:
mct += st.pop() * Math.min(st.peek(), arr[i]);12 / \ 6 4 / \ 2 3[Integer.MAX_VALUE, 6, 4]=> 源数组已遍历完,栈中还有较多数据,那么依次出栈做计算:while (st.size() > 2) mct += st.pop() * st.peek();24 / \ 6 12 / \ 6 4 / \ 2 3
可见,栈顶存的一直是当时能找到的最小值,也是二叉树某侧的叶子节点最大值,可以直接参与乘法运算。
再随便看一下全部递增和全部递减的数据的构造过程:
[1,2,3,4]:
[Integer.MAX_VALUE, 1], 2 =>while (arr[i] >= st.peek()) mct += st.pop() * Math.min(st.peek(), arr[i]);
2
/ \
1 2[Integer.MAX_VALUE, 2], 3 =>while (arr[i] >= st.peek()) mct += st.pop() * Math.min(st.peek(), arr[i]);
6
/ \
2 3
/ \
1 2[Integer.MAX_VALUE, 3], 4 =>while (arr[i] >= st.peek()) mct += st.pop() * Math.min(st.peek(), arr[i]);
12
/ \
6 4
/ \
2 3
/ \
1 2[4,3,2,1]:
[Integer.MAX_VALUE, 4, 3, 2, 1] =>while (st.size() > 2) mct += st.pop() * st.peek();
2
/ \
2 1[Integer.MAX_VALUE, 4, 3, 2] =>while (st.size() > 2) mct += st.pop() * st.peek();
6
/ \
3 2
/ \
2 1[Integer.MAX_VALUE, 4, 3] =>while (st.size() > 2) mct += st.pop() * st.peek();
12
/ \
4 6
/ \
3 2
/ \
2 1都能正确构造出正确的最小 mct 树。
其余情况其实最终都可以归并到这些情况之中。
代码
class Solution {
public int mctFromLeafValues(int[] arr) {
Stack<Integer> st = new Stack();
st.push(Integer.MAX_VALUE);
int mct = 0;
for (int i = 0; i < arr.length; i++) {
while (arr[i] >= st.peek()) {
mct += st.pop() * Math.min(st.peek(), arr[i]);
}
st.push(arr[i]);
}
while (st.size() > 2) {
mct += st.pop() * st.peek();
}
return mct;
}
}统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 6224 | 9840 | 63.3% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




