1161-最大层内元素和(Maximum Level Sum of a Binary Tree)
发表于：2021-12-03 | 分类： 中等
字数统计: 1.9k | 阅读时长: 8分钟 | 阅读量：

原文链接: https://leetcode-cn.com/problems/maximum-level-sum-of-a-binary-tree

英文原文

Given the root of a binary tree, the level of its root is 1, the level of its children is 2, and so on.

Return the smallest level x such that the sum of all the values of nodes at level x is maximal.

 

Example 1:

Input: root = [1,7,0,7,-8,null,null]
Output: 2
Explanation: 
Level 1 sum = 1.
Level 2 sum = 7 + 0 = 7.
Level 3 sum = 7 + -8 = -1.
So we return the level with the maximum sum which is level 2.

Example 2:

Input: root = [989,null,10250,98693,-89388,null,null,null,-32127]
Output: 2

 

Constraints:

  • The number of nodes in the tree is in the range [1, 104].
  • -105 <= Node.val <= 105

中文题目

给你一个二叉树的根节点 root。设根节点位于二叉树的第 1 层，而根节点的子节点位于第 2 层，依此类推。

请你找出层内元素之和 最大 的那几层（可能只有一层）的层号，并返回其中 最小 的那个。

 

示例 1：

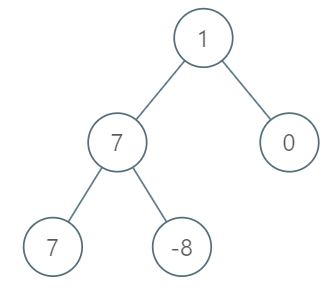
输入：root = [1,7,0,7,-8,null,null]
输出：2
解释：
第 1 层各元素之和为 1，
第 2 层各元素之和为 7 + 0 = 7，
第 3 层各元素之和为 7 + -8 = -1，
所以我们返回第 2 层的层号，它的层内元素之和最大。

示例 2：

输入：root = [989,null,10250,98693,-89388,null,null,null,-32127]
输出：2

 

提示：

  • 树中的节点数介于 1 和 10^4 之间
  • -10^5 <= node.val <= 10^5

通过代码

官方题解

概述

遍历树的两种通用策略：

  • 深度优先遍历（DFS）

    这种方法以深度 depth 优先为策略，从根节点开始一直遍历到某个叶子节点，然后回到根节点，再遍历另外一个分支。

    根据根节点，左子节点和右子节点的访问顺序又可以将 DFS 细分为先序遍历 preorder，中序遍历 inorder 和后序遍历 postorder。

    DFS 遍历通常有三种实现方式：递归 recursion，迭代 iteration，Morris，其中最简单的是递归。

{:width=500}

  • 广度优先遍历（BFS）

    按照高度顺序，从上往下逐层遍历节点。先遍历上层节点再遍历下层节点。

    最标准的实现方法是使用队列进行迭代。

下图中按照不同的方法遍历对应子树，得到的遍历顺序都是 1-2-3-4-5。根据不同子树结构比较不同遍历方法的特点。

{:width=500}

本题可以使用两种策略解决：DFS 和 BFS。这里使用 DFS 的中序遍历和队列实现的 BFS 解答。

方法一：DFS：递归实现的中序遍历

递归实现的中序遍历非常简单：遵循 Left->Node->Right 的顺序。例如：首先递归访问 左孩子，然后访问父节点，再递归访问 右孩子。

遍历时需要记录当前层节点之和。由于 Java 中 HashMap 的性能问题，在 Java 中使用数组，在 Python 中使用 hashmap。

算法

  • 创建方法 inorder(node, level)，实现递归的中序遍历。该方法输入当前节点和当前节点层级，然后递归更新 level_sum[level]。

  • 返回数组 level_sum 的最大值。

[solution1-Pyhton]
from collections import defaultdict
class Solution:
    def maxLevelSum(self, root: TreeNode) -> int:
        def inorder(node, level):
            if node:
                inorder(node.left, level + 1)
                level_sum[level] += node.val
                inorder(node.right, level + 1)
            
        level_sum = defaultdict(int)
        inorder(root, 1)
        return max(level_sum, key = level_sum.get)
[solution1-Java]
class Solution {
  int n = 10000;
  int[] levelSum = new int[n];

  public void inorder(TreeNode node, int level) {
    if (node != null) {
      inorder(node.left, level + 1);
      levelSum[level] += node.val;
      inorder(node.right, level + 1);
    }
  }
  
  public int maxLevelSum(TreeNode root) {
    inorder(root, 1);

    int maxIdx = 0;
    for (int i = 0; i < n; ++i)
      maxIdx = levelSum[i] > levelSum[maxIdx] ? i : maxIdx;
    return maxIdx;
  }
}

复杂度分析

  • 时间复杂度：$\mathcal{O}(N)$，中序遍历每个节点只访问一次，然后遍历 level_sum。

  • 空间复杂度：$\mathcal{O}(10000) = \mathcal{O}(1)$ 为 Java 中 level_sum 的空间。$\mathcal{O}(D)$ 为 Python 的空间，其中 $D$ 是树的深度。树是平衡的情况下，空间复杂度为 $\mathcal{O}(\log N)$ ，最坏情况下为 $\mathcal{O}(N)$。

方法二：BFS：使用队列实现的层序遍历

DFS 的缺点是必须保存所有层节点之和，BFS 逐层计算之和不需要同时保存每层之和：

  • 初始 max_sum = 0。

  • 使用 BFS 逐层遍历，计算每层的累加和 curr_sum，在每层结束时更新 max_sum = max(max_sum, curr_sum)。

使用队列（先进先出结构）实现 BFS：

  1. 把当前层所有的节点压入队列。

  2. 遍历队列。每从队列中弹出一个节点，就将该节点的子节点压入队列。

{:width=500}

这种方法可以从根节点逐层遍历到叶节点，不过需要设置标记在每层末尾计算该层节点的累加和。

面试技巧。可以使用 标记 分离队列/链表/树中的节点。
例子：LRU Cache。

这里使用空节点作为每层结束的标记。

算法

  • 初始化变量：

    • 令当前层级与最大累加和层级为 1。
    • 令当前累加和为 0，最大累加和为根节点的值。
    • 使用空节点作为标记，初始化队列：压入根节点和标记节点，标记当前层数为 1。

  • 当前队列长度大于 1：

    • 从队列左端弹出一个节点。
    • 如果它不是标记节点，则在当前层继续：
      • 更新当前层累加和。
      • 将该节点的子节点压入队列右端。
    • 如果它是标记节点，则当前层结束。
      • 根据当前层累加和更新最大和。
      • 设置当前累加和为 0。
      • 层数加 1，向队列中压入标记节点，表示下一层节点结束。

  • 返回最大累加和层序号。

[solution2-Python]
from collections import deque
class Solution:
    def maxLevelSum(self, root: TreeNode) -> int:
        curr_level = max_level = 1
        max_sum = float('-inf')
        curr_sum = 0
        
        marker = None
        queue = deque([root, marker])
        
        while len(queue) > 1:
            x = queue.popleft()
            # continue current level
            if x != marker:
                curr_sum += x.val
                if x.left:
                    queue.append(x.left)
                if x.right:
                    queue.append(x.right)
            # end of current level, go to the next level
            else:
                if curr_sum > max_sum:
                    max_sum, max_level = curr_sum, curr_level  
                curr_sum = 0
                curr_level += 1
                queue.append(marker)
            
        return max_level
[solution2-Java]
class Solution {
  public int maxLevelSum(TreeNode root) {
    int currLevel = 1, maxLevel = 1;
    int maxSum = root.val, currSum = 0;

    LinkedList<TreeNode> queue = new LinkedList();
    TreeNode marker = null, x = root;
    queue.addLast(root);
    queue.addLast(marker);

    while (queue.size() > 1) {
      x = queue.removeFirst();
      // continue current level
      if (x != marker) {
        currSum += x.val;
        if (x.left != null) queue.addLast(x.left);
        if (x.right != null) queue.addLast(x.right);
      }
      // end of current level, go to the next level
      else {
        if (currSum > maxSum) {
          maxSum = currSum;
          maxLevel = currLevel;
        }
        currSum = 0;
        currLevel++;
        queue.addLast(marker);
      }
    }

    return maxLevel;
  }
}

复杂度分析

  • 时间复杂度：$\mathcal{O}(N)$，每个节点只被访问两次，入队列和出队列。

  • 空间复杂度：$\mathcal{O}(N)$，队列的存储空间。任意时刻，队列最多只包含一层的所有节点。完美树中一层节点最多有 $(N + 1)/2$ 个。

方法三：BFS：简洁的 Python 解法

重写方法二中 Python 代码。

[solution3-Python]
class Solution:
    def maxLevelSum(self, root: TreeNode) -> int:
        curr_level = max_level = 1
        max_sum = float('-inf')
        queue = [root, ]
        
        while queue:
            # sum up all the nodes on the current level
            curr_sum = sum([x.val for x in queue])
            # update max_sum 
            if curr_sum > max_sum:
                max_sum, max_level = curr_sum, curr_level
            # build next level
            queue = [y for x in queue for y in [x.left, x.right] if y]
            curr_level += 1
            
        return max_level

复杂度分析

  • 时间复杂度：$\mathcal{O}(N)$。

  • 空间复杂度：$\mathcal{O}(N)$，队列的存储空间。任意时刻，队列最多只包含一层的所有节点。完美树中一层节点最多有 $(N + 1)/2$ 个。

统计信息

通过次数 提交次数 AC比率
10975 17340 63.3%

提交历史

提交时间 提交结果 执行时间 内存消耗 语言
广度优先搜索 树 二叉树
上一篇:
1038-把二叉搜索树转换为累加树(Binary Search Tree to Greater Sum Tree)
下一篇:
1162-地图分析(As Far from Land as Possible)
本文目录
本文目录
    •
    本站总访问量： 次 |
    Copyright © 2020 - 2021 枫奇丶宛南 | Powered by Hexo | Theme Bamboo