原文链接: https://leetcode-cn.com/problems/queens-that-can-attack-the-king

英文原文

On an 8x8 chessboard, there can be multiple Black Queens and one White King.

Given an array of integer coordinates queens that represents the positions of the Black Queens, and a pair of coordinates king that represent the position of the White King, return the coordinates of all the queens (in any order) that can attack the King.

 

Example 1:

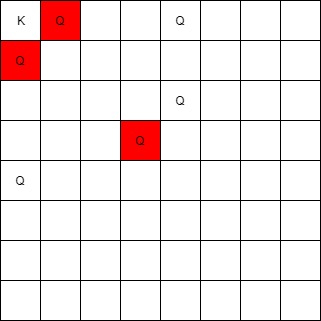
Input: queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
Output: [[0,1],[1,0],[3,3]]
Explanation:  
The queen at [0,1] can attack the king cause they're in the same row. 
The queen at [1,0] can attack the king cause they're in the same column. 
The queen at [3,3] can attack the king cause they're in the same diagnal. 
The queen at [0,4] can't attack the king cause it's blocked by the queen at [0,1]. 
The queen at [4,0] can't attack the king cause it's blocked by the queen at [1,0]. 
The queen at [2,4] can't attack the king cause it's not in the same row/column/diagnal as the king.

Example 2:

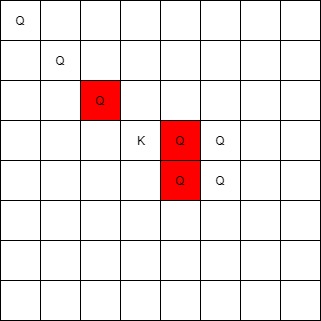
Input: queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
Output: [[2,2],[3,4],[4,4]]

Example 3:

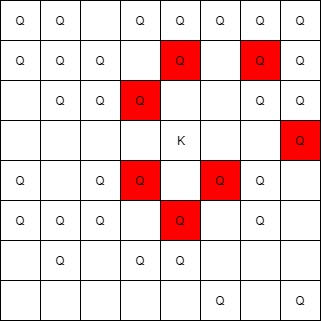
Input: queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
Output: [[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]

 

Constraints:

• 1 <= queens.length <= 63
• queens[i].length == 2
• 0 <= queens[i][j] < 8
• king.length == 2
• 0 <= king[0], king[1] < 8
• At most one piece is allowed in a cell.

中文题目

在一个 8x8 的棋盘上，放置着若干「黑皇后」和一个「白国王」。

「黑皇后」在棋盘上的位置分布用整数坐标数组 queens 表示，「白国王」的坐标用数组 king 表示。

「黑皇后」的行棋规定是：横、直、斜都可以走，步数不受限制，但是，不能越子行棋。

请你返回可以直接攻击到「白国王」的所有「黑皇后」的坐标（任意顺序）。

 

示例 1：

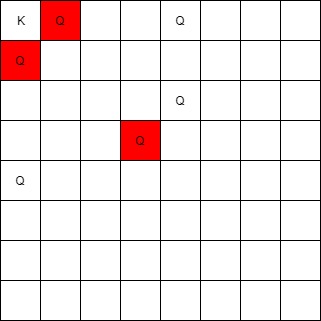
输入：queens = [[0,1],[1,0],[4,0],[0,4],[3,3],[2,4]], king = [0,0]
输出：[[0,1],[1,0],[3,3]]
解释： 
[0,1] 的皇后可以攻击到国王，因为他们在同一行上。 
[1,0] 的皇后可以攻击到国王，因为他们在同一列上。 
[3,3] 的皇后可以攻击到国王，因为他们在同一条对角线上。 
[0,4] 的皇后无法攻击到国王，因为她被位于 [0,1] 的皇后挡住了。 
[4,0] 的皇后无法攻击到国王，因为她被位于 [1,0] 的皇后挡住了。 
[2,4] 的皇后无法攻击到国王，因为她和国王不在同一行/列/对角线上。

示例 2：

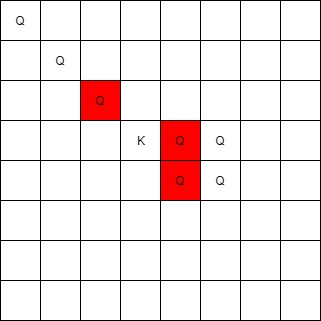
输入：queens = [[0,0],[1,1],[2,2],[3,4],[3,5],[4,4],[4,5]], king = [3,3]
输出：[[2,2],[3,4],[4,4]]

示例 3：

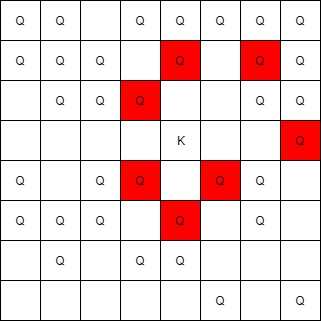
输入：queens = [[5,6],[7,7],[2,1],[0,7],[1,6],[5,1],[3,7],[0,3],[4,0],[1,2],[6,3],[5,0],[0,4],[2,2],[1,1],[6,4],[5,4],[0,0],[2,6],[4,5],[5,2],[1,4],[7,5],[2,3],[0,5],[4,2],[1,0],[2,7],[0,1],[4,6],[6,1],[0,6],[4,3],[1,7]], king = [3,4]
输出：[[2,3],[1,4],[1,6],[3,7],[4,3],[5,4],[4,5]]

 

提示：

• 1 <= queens.length <= 63
• queens[i].length == 2
• 0 <= queens[i][j] < 8
• king.length == 2
• 0 <= king[0], king[1] < 8
• 一个棋盘格上最多只能放置一枚棋子。

通过代码

高赞题解

思路就是以国王为起点往八个方向迭代，循环结束条件为出界((x < 0 || x >= 8) || (y < 0 || y >= 8))或者在这个方向上找到第一个皇后，那么结束当前这个循环，继续迭代下一个方向。

class Solution {
    public List<List<Integer>> queensAttacktheKing(int[][] queens, int[] king) {
        List<List<Integer>> res = new LinkedList<>();
        //标志数组
        boolean[][] flag = new boolean[8][8];
        for(int[] queen : queens)
            flag[queen[0]][queen[1]] = true;
        //8个方向                         右     左    上    下    右上   右下   左上    左下   
        int[][] direction = new int[][]{{1,0},{-1,0},{0,1},{0,-1},{1,1},{1,-1},{-1,1},{-1,-1}};
        //从第一个方向开始到第八个方向
        for(int i = 0;i < direction.length;i++){
            //起始位置为king的坐标,找到第一个皇后停止这个方向的查找，或者直到出界
            for(int x = king[0],y = king[1];x >= 0 && x < 8 && y >= 0 && y < 8;x += direction[i][0],y += direction[i][1]){
                if(flag[x][y]){
                    res.add(Arrays.asList(x,y));
                    break;
                }
            }
        }
        
        return res;
    }
}

统计信息

通过次数	提交次数	AC比率
6150	9124	67.4%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言