原文链接: https://leetcode-cn.com/problems/maximum-side-length-of-a-square-with-sum-less-than-or-equal-to-threshold

英文原文

Given a m x n matrix mat and an integer threshold. Return the maximum side-length of a square with a sum less than or equal to threshold or return 0 if there is no such square.

 

Example 1:

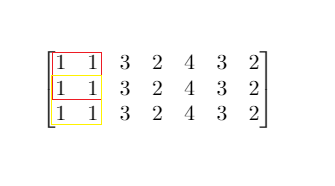
Input: mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
Output: 2
Explanation: The maximum side length of square with sum less than 4 is 2 as shown.

Example 2:

Input: mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
Output: 0

Example 3:

Input: mat = [[1,1,1,1],[1,0,0,0],[1,0,0,0],[1,0,0,0]], threshold = 6
Output: 3

Example 4:

Input: mat = [[18,70],[61,1],[25,85],[14,40],[11,96],[97,96],[63,45]], threshold = 40184
Output: 2

 

Constraints:

• 1 <= m, n <= 300
• m == mat.length
• n == mat[i].length
• 0 <= mat[i][j] <= 10000
• 0 <= threshold <= 10^5

中文题目

给你一个大小为 m x n 的矩阵 mat 和一个整数阈值 threshold。

请你返回元素总和小于或等于阈值的正方形区域的最大边长；如果没有这样的正方形区域，则返回 0 。
 

示例 1：

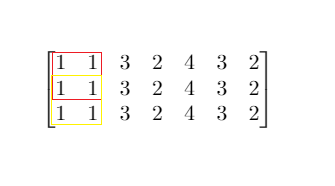
输入：mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
输出：2
解释：总和小于或等于 4 的正方形的最大边长为 2，如图所示。

示例 2：

输入：mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
输出：0

示例 3：

输入：mat = [[1,1,1,1],[1,0,0,0],[1,0,0,0],[1,0,0,0]], threshold = 6
输出：3

示例 4：

输入：mat = [[18,70],[61,1],[25,85],[14,40],[11,96],[97,96],[63,45]], threshold = 40184
输出：2

 

提示：

• 1 <= m, n <= 300
• m == mat.length
• n == mat[i].length
• 0 <= mat[i][j] <= 10000
• 0 <= threshold <= 10^5

通过代码

高赞题解

解法一 前缀和

思路

遍历所有可能的正方形区域，具体的算法流程是：1.考虑正方形的边长从 1 到 $Min(M,N)$（M 为矩阵长度，N 为矩阵宽度）2.考虑正方形右下角的坐标从 (0, 0) 到 (M, N) 3.判断正方形是否存在（可能会超出边界，通过左上角坐标判断），如果存在则验证该正方形区域的元素总和。

下面引入二维前缀和的计算方法，通过预处理可以在 $O(1)$ 时间内计算出一块区域内元素的总和。

首先是预处理，在 $O(N^2)$ 时间内计算出二维前缀和 dp[i][j]：从 (0, 0) 到 (i, j) 内元素的总和。

已知 dp[i][j] 必定包含一个元素 mat[i][j]，假设我们已经计算出部分前缀和 dp[x][y]（x < i 且 y < j），那么 dp[i][j] = mat[i][j] + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1]。

下面通过一组动画来理解这个过程（图片较大，请点击左下角播放）：

我们需要计算黑色虚线区域即 dp[i][j]，先加上右下角元素mat[i][j]，接着加上mat[i][j]上方区域的前缀和dp[i - 1][j]以及左边区域的前缀和dp[i][j - 1]，但左上角一块区域被加了两次，因此还要再扣去这块区域dp[i - 1][j - 1]。

<,,,>

预处理完二维前缀和，我们可以逆向这个过程，计算出某一块特定区域内元素总和。例如计算下面的红色区域，其右下角坐标为 (i, j)，长度和宽度为 k，则可以将绿色区域 dp[i][j] 减去红色区域相邻的上方区域dp[i - k][j]以及相邻的左边区域dp[i][j - k]，最后补上被多减一次的左上方区域dp[i - k][j - k]。

图示（图片较大，请点击左下角播放）：

<,,,,>

代码

class Solution {
    public int maxSideLength(int[][] mat, int threshold) {
        int m = mat.length, n = mat[0].length;
        int[][] dp = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                dp[i][j] = mat[i - 1][j - 1] + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];
            }
        }
        int ans = 0;
        for (int k = 1; k <= Math.min(m, n); k++) {
            for (int i = 1; i <= m; i++) {
                for (int j = 1; j <= n; j++) {
                    if (i - k < 0 || j - k < 0) {
                        continue;
                    }
                    int tmp = dp[i][j] - dp[i - k][j] - dp[i][j - k] + dp[i - k][j - k];
                    if (tmp <= threshold) {
                        ans = Math.max(ans, k);
                    }
                }
            }
        }
        return ans;
    }
}

复杂度分析

• 时间复杂度：$O(min(M, N) * M * N)$，其中 M 为矩阵长度，N 为矩阵宽度。

解法二 前缀和 + 二分

思路

查找的正方形的边长越长，其计算出来的元素总和越大。

我们可以二分正方形的边长，在满足阈值条件下尽可能地扩大正方形的边长，其等价于在升序数组中查找一个小于等于 k 的最大元素。

二分的具体思路：

• 控制 l 到 h 都是可能可能的值
• 如果 mid 满足阈值条件，则 l = mid，l 可能是答案，不能直接舍去。
• 如果 mid 不满足阈值条件，则 h = mid - 1。
• 当 l = h 或 l + 1 = h 时跳出循环（小提示：l = mid 可能造成死循环，通过 l + 1 == h 条件跳出），判断 l 和 h 两个是最优解。

代码

class Solution {
    int m, n;
    int[][] dp;
    public int maxSideLength(int[][] mat, int threshold) {
        m = mat.length;
        n = mat[0].length;
        dp = new int[m + 1][n + 1];
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                dp[i][j] = mat[i - 1][j - 1] + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];
            }
        }
        int l = 0, h = Math.min(m, n);
        while (l <= h) {
            int mid = l + (h - l) / 2;
            if (l == h || l + 1 == h) {
                break;
            }
            if (help(mid, threshold)) {
                l = mid;
            } else {
                h = mid - 1;
            }
        }
        if (help(h, threshold)) {
            return h;
        } else {
            return l;
        }
    }
    public boolean help(int k, int threshold) {
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (i - k < 0 || j - k < 0) {
                    continue;
                }
                if (dp[i][j] - dp[i - k][j] - dp[i][j - k] + dp[i - k][j - k] <= threshold) {
                    return true;
                }
            }
        }
        return false;
    }
}

复杂度分析

• 时间复杂度：$O(log(min(M, N)) * M * N)$，其中 M 为矩阵长度，N 为矩阵宽度。

---

如果该题解对你有帮助，点个赞再走呗~

统计信息

通过次数	提交次数	AC比率
6379	13446	47.4%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言