原文链接: https://leetcode-cn.com/problems/sum-of-nodes-with-even-valued-grandparent

英文原文

Given the root of a binary tree, return the sum of values of nodes with an even-valued grandparent. If there are no nodes with an even-valued grandparent, return 0.

A grandparent of a node is the parent of its parent if it exists.

 

Example 1:

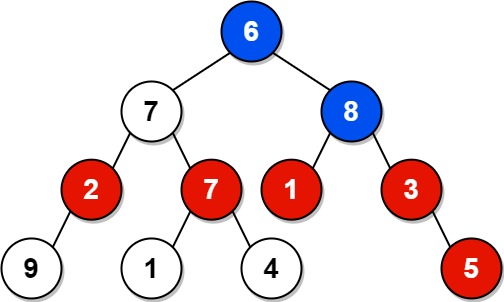
Input: root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
Output: 18
Explanation: The red nodes are the nodes with even-value grandparent while the blue nodes are the even-value grandparents.

Example 2:

Input: root = [1]
Output: 0

 

Constraints:

• The number of nodes in the tree is in the range [1, 104].
• 1 <= Node.val <= 100

中文题目

给你一棵二叉树，请你返回满足以下条件的所有节点的值之和：

• 该节点的祖父节点的值为偶数。（一个节点的祖父节点是指该节点的父节点的父节点。）

如果不存在祖父节点值为偶数的节点，那么返回 0 。

 

示例：

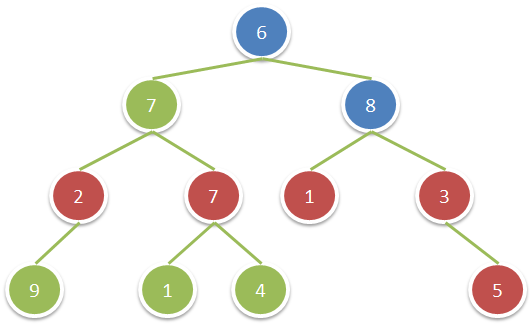
输入：root = [6,7,8,2,7,1,3,9,null,1,4,null,null,null,5]
输出：18
解释：图中红色节点的祖父节点的值为偶数，蓝色节点为这些红色节点的祖父节点。

 

提示：

• 树中节点的数目在 1 到 10^4 之间。
• 每个节点的值在 1 到 100 之间。

通过代码

高赞题解

方法一：深度优先搜索

我们可以通过深度优先搜索找出所有满足题目要求的节点。

具体地，在进行搜索时，搜索状态除了当前节点之外，还需要存储该节点的祖父节点和父节点，即三元组 (grandparent, parent, node)。如果节点 grandparent 的值为偶数，那么就将节点 node 的值加入答案。在这之后，我们继续搜索节点 node 的左孩子 (parent, node, node.left) 以及右孩子 (parent, node, node.right)，直到搜索结束。

[sol1-C++]
class Solution {
private:
    int ans = 0;
    
public:
    void dfs(TreeNode* grandparent, TreeNode* parent, TreeNode* node) {
        if (!node) {
            return;
        }
        if (grandparent->val % 2 == 0) {
            ans += node->val;
        }
        dfs(parent, node, node->left);
        dfs(parent, node, node->right);
    }
    
    int sumEvenGrandparent(TreeNode* root) {
        if (root->left) {
            dfs(root, root->left, root->left->left);
            dfs(root, root->left, root->left->right);
        }
        if (root->right) {
            dfs(root, root->right, root->right->left);
            dfs(root, root->right, root->right->right);
        }
        return ans;
    }
};

[sol1-Python3]
class Solution:
    def sumEvenGrandparent(self, root: TreeNode) -> int:
        ans = 0

        def dfs(grandparent, parent, node):
            if not node:
                return
            if grandparent.val % 2 == 0:
                nonlocal ans
                ans += node.val
            dfs(parent, node, node.left)
            dfs(parent, node, node.right)
        
        if root.left:
            dfs(root, root.left, root.left.left)
            dfs(root, root.left, root.left.right)
        if root.right:
            dfs(root, root.right, root.right.left)
            dfs(root, root.right, root.right.right)
        
        return ans

然而这种搜索状态的表示方法不够通用。在上面的代码中，我们需要使用两次 if 进行四次搜索函数的调用，才能完成树中所有节点的搜索。那么如何将代码写得更加通用和美观呢？

我们想一想为什么需要在代码中使用两次 if 进行四次搜索：由于根节点没有父节点，根节点的子节点没有祖父节点，那么搜索状态中的grandparent 和 parent 无法进行表示，因此我们必须从根节点的孙子节点（即子节点的子节点）开始搜索。而我们发现，在搜索状态三元组 (grandparent, parent, node) 中，grandparent 和 parent 这两项我们只使用了它的值，而不使用节点本身，因此我们可以在搜索状态中用值来替换这些节点。

我们可以假设根节点有一个虚拟的祖父节点和父节点，它们的值都为 1。在搜索时，我们使用三元组 (gp_val, p_val, node) 表示搜索状态，其中 gp_val 和 p_val 分别表示祖父节点和父节点的值，node 表示当前节点。这样以来，我们就可以直接从状态 (1, 1, root) 开始直接对根节点进行搜索了。

[sol2-C++]
class Solution {
private:
    int ans = 0;
    
public:
    void dfs(int gp_val, int p_val, TreeNode* node) {
        if (!node) {
            return;
        }
        if (gp_val % 2 == 0) {
            ans += node->val;
        }
        dfs(p_val, node->val, node->left);
        dfs(p_val, node->val, node->right);
    }
    
    int sumEvenGrandparent(TreeNode* root) {
        dfs(1, 1, root);
        return ans;
    }
};

[sol2-Python3]
class Solution:
    def sumEvenGrandparent(self, root: TreeNode) -> int:
        ans = 0

        def dfs(gp_val, p_val, node):
            if not node:
                return
            if gp_val % 2 == 0:
                nonlocal ans
                ans += node.val
            dfs(p_val, node.val, node.left)
            dfs(p_val, node.val, node.right)
        
        dfs(1, 1, root)
        return ans

复杂度分析

• 时间复杂度：$O(N)$，其中 $N$ 是树中的节点个数。

• 空间复杂度：$O(H)$，其中 $H$ 是树的高度。

方法二：广度优先搜索

我们也可以换一种思考方式。既然要找出祖父节点的值为偶数的节点，我们不如找到所有值为偶数的节点，并对这些节点的孙子节点（即子节点的子节点）统计答案。

这样我们就可以使用广度优先搜索遍历整棵树，当我们找到一个值为偶数的节点时，我们将该节点的所有孙子节点的值加入答案。

[sol3-C++]
class Solution {
public:
    int sumEvenGrandparent(TreeNode* root) {
        queue<TreeNode*> q;
        q.push(root);
        int ans = 0;
        while (!q.empty()) {
            TreeNode* node = q.front();
            q.pop();
            if (node->val % 2 == 0) {
                if (node->left) {
                    if (node->left->left) {
                        ans += node->left->left->val;
                    }
                    if (node->left->right) {
                        ans += node->left->right->val;
                    }
                }
                if (node->right) {
                    if (node->right->left) {
                        ans += node->right->left->val;
                    }
                    if (node->right->right) {
                        ans += node->right->right->val;
                    }
                }
            }
            if (node->left) {
                q.push(node->left);
            }
            if (node->right) {
                q.push(node->right);
            }
        }
        return ans;
    }
};

[sol3-Python3]
class Solution:
    def sumEvenGrandparent(self, root: TreeNode) -> int:
        q = collections.deque([root])
        ans = 0
        while len(q) > 0:
            node = q.popleft()
            if node.val % 2 == 0:
                if node.left:
                    if node.left.left:
                        ans += node.left.left.val
                    if node.left.right:
                        ans += node.left.right.val
                if node.right:
                    if node.right.left:
                        ans += node.right.left.val
                    if node.right.right:
                        ans += node.right.right.val
            if node.left:
                q.append(node.left)
            if node.right:
                q.append(node.right)
        return ans

复杂度分析

• 时间复杂度：$O(N)$，其中 $N$ 是树中的节点个数。

• 空间复杂度：$O(N)$。

统计信息

通过次数	提交次数	AC比率
13256	16359	81.0%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言