原文链接: https://leetcode-cn.com/problems/sort-the-matrix-diagonally

英文原文

A matrix diagonal is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix's end. For example, the matrix diagonal starting from mat[2][0], where mat is a 6 x 3 matrix, includes cells mat[2][0], mat[3][1], and mat[4][2].

Given an m x n matrix mat of integers, sort each matrix diagonal in ascending order and return the resulting matrix.

 

Example 1:

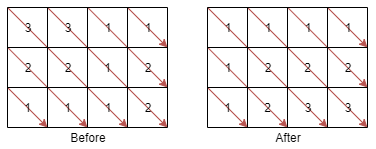
Input: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
Output: [[1,1,1,1],[1,2,2,2],[1,2,3,3]]

Example 2:

Input: mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
Output: [[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 100
• 1 <= mat[i][j] <= 100

中文题目

矩阵对角线 是一条从矩阵最上面行或者最左侧列中的某个元素开始的对角线，沿右下方向一直到矩阵末尾的元素。例如，矩阵 mat 有 6 行 3 列，从 mat[2][0] 开始的 矩阵对角线 将会经过 mat[2][0]、mat[3][1] 和 mat[4][2] 。

给你一个 m * n 的整数矩阵 mat ，请你将同一条 矩阵对角线 上的元素按升序排序后，返回排好序的矩阵。

 

示例 1：

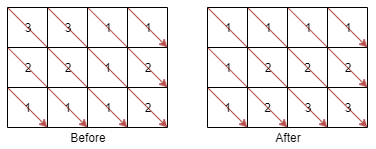
输入：mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
输出：[[1,1,1,1],[1,2,2,2],[1,2,3,3]]

示例 2：

输入：mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
输出：[[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]

 

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 100
• 1 <= mat[i][j] <= 100

通过代码

高赞题解

利用左对角线元素 坐标 i-j 相等的特性（右对角线元素 i+j 相等）
把同一斜边的元素放到一个数组里排序
再放回去

class Solution {
public:
    vector<vector<int>> diagonalSort(vector<vector<int>>& mat) {
        int n = mat.size(), m = mat[0].size();
        unordered_map<int, vector<int>> vs;
        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j)
                vs[i - j].emplace_back(mat[i][j]);
        }
        for (auto& v : vs) sort(v.second.rbegin(), v.second.rend());

        for (int i = 0; i < n; ++i) {
            for (int j = 0; j < m; ++j) {
                mat[i][j] = vs[i - j].back();
                vs[i - j].pop_back();
            }
        }
        return mat;
    }
};

统计信息

通过次数	提交次数	AC比率
7276	9427	77.2%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言