原文链接: https://leetcode-cn.com/problems/clone-graph

英文原文

Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a value (int) and a list (List[Node]) of its neighbors.

class Node {
    public int val;
    public List<Node> neighbors;
}

 

Test case format:

For simplicity, each node's value is the same as the node's index (1-indexed). For example, the first node with val == 1, the second node with val == 2, and so on. The graph is represented in the test case using an adjacency list.

An adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

 

Example 1:

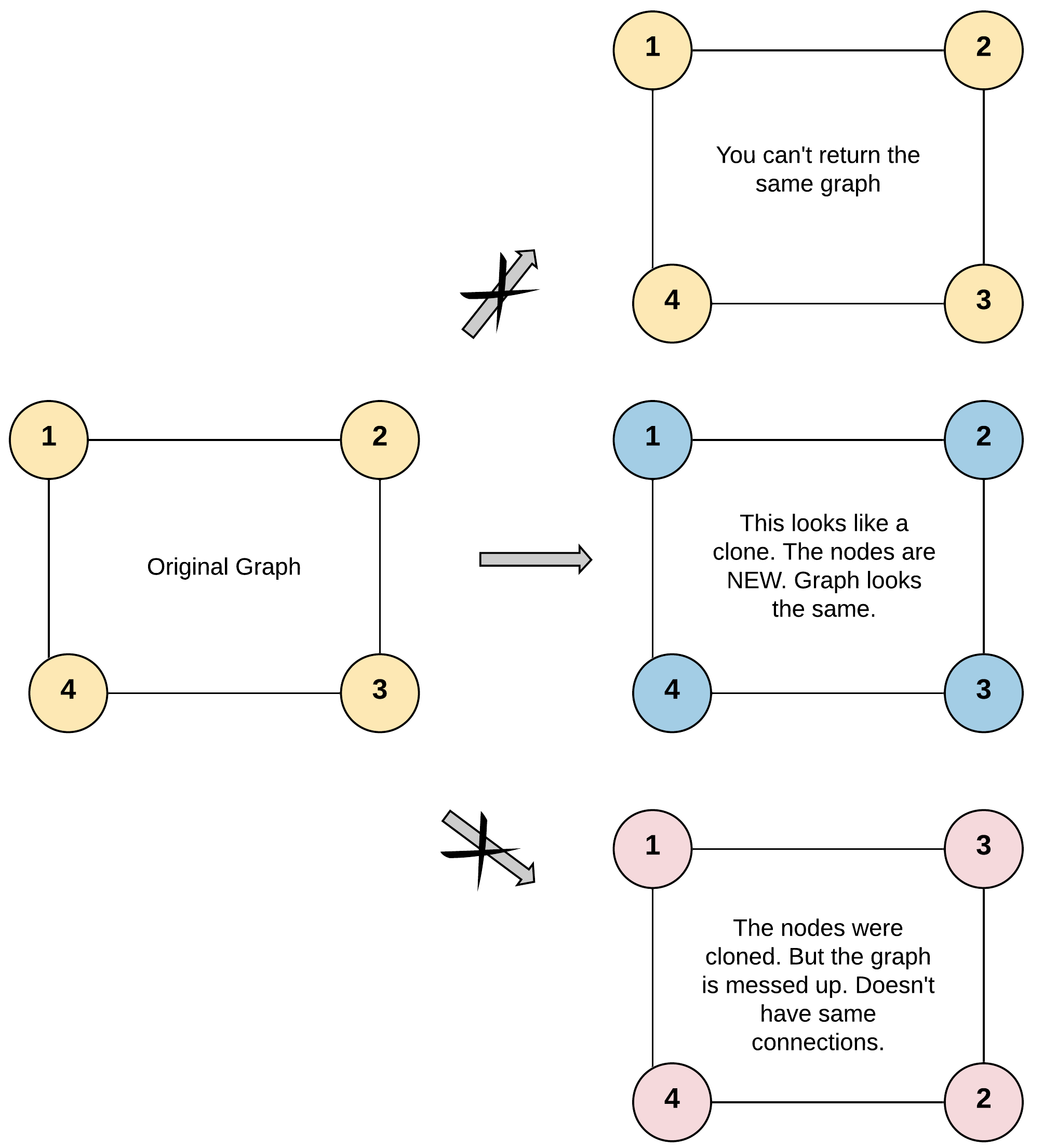
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2:

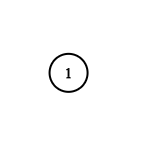
Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3:

Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.

Example 4:

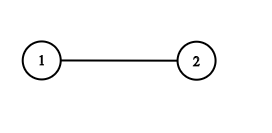
Input: adjList = [[2],[1]]
Output: [[2],[1]]

 

Constraints:

• The number of nodes in the graph is in the range [0, 100].
• 1 <= Node.val <= 100
• Node.val is unique for each node.
• There are no repeated edges and no self-loops in the graph.
• The Graph is connected and all nodes can be visited starting from the given node.

中文题目

给你无向 连通 图中一个节点的引用，请你返回该图的 深拷贝（克隆）。

图中的每个节点都包含它的值 val（int） 和其邻居的列表（list[Node]）。

class Node {
    public int val;
    public List<Node> neighbors;
}

 

测试用例格式：

简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为 1（val = 1），第二个节点值为 2（val = 2），以此类推。该图在测试用例中使用邻接列表表示。

邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。

给定节点将始终是图中的第一个节点（值为 1）。你必须将 给定节点的拷贝 作为对克隆图的引用返回。

 

示例 1：

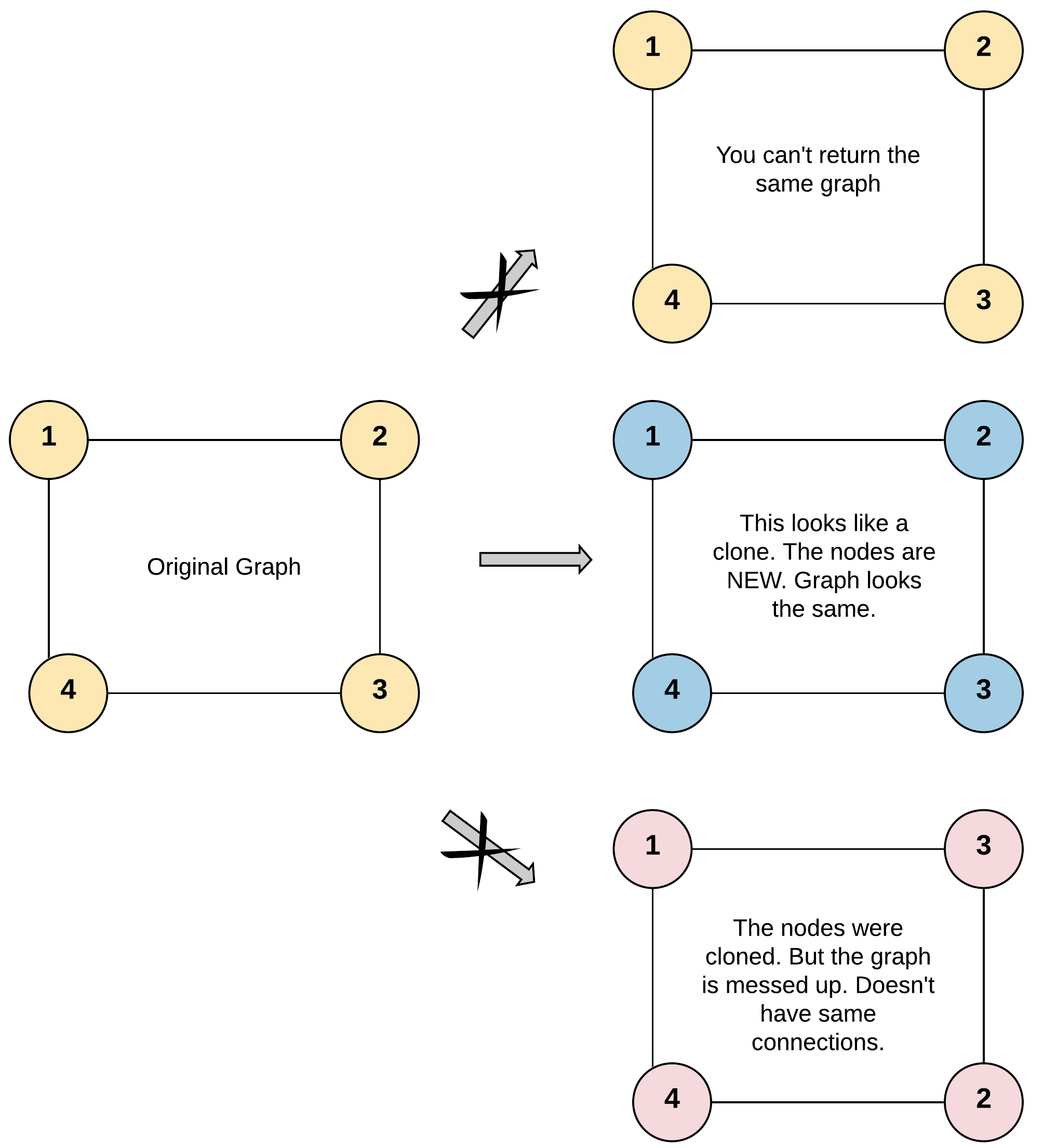
输入：adjList = [[2,4],[1,3],[2,4],[1,3]]
输出：[[2,4],[1,3],[2,4],[1,3]]
解释：
图中有 4 个节点。
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

示例 2：

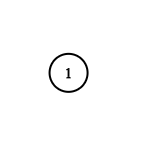
输入：adjList = [[]]
输出：[[]]
解释：输入包含一个空列表。该图仅仅只有一个值为 1 的节点，它没有任何邻居。

示例 3：

输入：adjList = []
输出：[]
解释：这个图是空的，它不含任何节点。

示例 4：

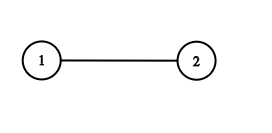
输入：adjList = [[2],[1]]
输出：[[2],[1]]

 

提示：

1. 节点数不超过 100 。
2. 每个节点值 Node.val 都是唯一的，1 <= Node.val <= 100。
3. 无向图是一个简单图，这意味着图中没有重复的边，也没有自环。
4. 由于图是无向的，如果节点 p 是节点 q 的邻居，那么节点 q 也必须是节点 p 的邻居。
5. 图是连通图，你可以从给定节点访问到所有节点。

通过代码

高赞题解

解题思路:

这道题就是遍历整个图，所以遍历时候要记录已经访问点，我们用一个字典记录。

所以，遍历方法就有两种。

思路一:DFS (深度遍历)

思路二:BFS (广度遍历)

!!! 大家重点掌握，后面图遍历都和这个有关系！

代码:

思路一:

[1]

class Solution:

    def cloneGraph(self, node: 'Node') -> 'Node':

        lookup = {}



        def dfs(node):

            #print(node.val)

            if not node: return

            if node in lookup:

                return lookup[node]

            clone = Node(node.val, [])

            lookup[node] = clone

            for n in node.neighbors:

                clone.neighbors.append(dfs(n))

            

            return clone



        return dfs(node)

[1]

class Solution {

    public Node cloneGraph(Node node) {

        Map<Node, Node> lookup = new HashMap<>();

        return dfs(node, lookup);

    }



    private Node dfs(Node node, Map<Node,Node> lookup) {

        if (node == null) return null;

        if (lookup.containsKey(node)) return lookup.get(node);

        Node clone = new Node(node.val, new ArrayList<>());

        lookup.put(node, clone);

        for (Node n : node.neighbors)clone.neighbors.add(dfs(n,lookup));

        return clone;

    }

}

思路二:

[2]

class Solution:

    def cloneGraph(self, node: 'Node') -> 'Node':

        from collections import deque

        lookup = {}



        def bfs(node):

            if not node: return

            clone = Node(node.val, [])

            lookup[node] = clone

            queue = deque()

            queue.appendleft(node)

            while queue:

                tmp = queue.pop()

                for n in tmp.neighbors:

                    if n not in lookup:

                        lookup[n] = Node(n.val, [])

                        queue.appendleft(n)

                    lookup[tmp].neighbors.append(lookup[n])

            return clone



        return bfs(node)

[2]

class Solution {

    public Node cloneGraph(Node node) {

        if (node == null) return null;

        Map<Node, Node> lookup = new HashMap<>();

        Node clone = new Node(node.val, new ArrayList<>());

        lookup.put(node, clone);

        Deque<Node> queue = new LinkedList<>();

        queue.offer(node);

        while (!queue.isEmpty()) {

            Node tmp = queue.poll();

            for (Node n : tmp.neighbors) {

                if (!lookup.containsKey(n)) {

                    lookup.put(n, new Node(n.val, new ArrayList<>()));

                    queue.offer(n);

                }

                lookup.get(tmp).neighbors.add(lookup.get(n));

            }

        }

        return clone;

    }

}

统计信息

通过次数	提交次数	AC比率
77338	114126	67.8%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
复制带随机指针的链表	中等