原文链接: https://leetcode-cn.com/problems/maximum-product-of-splitted-binary-tree

英文原文

Given the root of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.

Return the maximum product of the sums of the two subtrees. Since the answer may be too large, return it modulo 109 + 7.

Note that you need to maximize the answer before taking the mod and not after taking it.

 

Example 1:

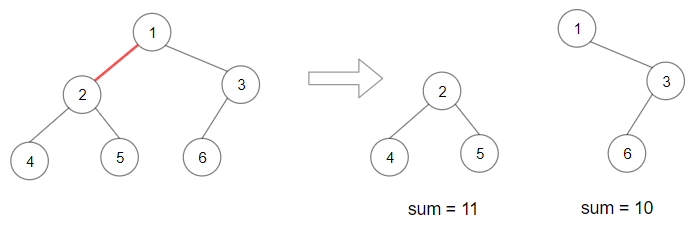
Input: root = [1,2,3,4,5,6]
Output: 110
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)

Example 2:

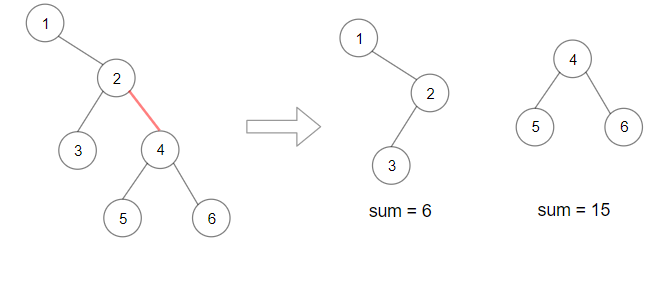
Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90
Explanation: Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)

Example 3:

Input: root = [2,3,9,10,7,8,6,5,4,11,1]
Output: 1025

Example 4:

Input: root = [1,1]
Output: 1

 

Constraints:

• The number of nodes in the tree is in the range [2, 5 * 104].
• 1 <= Node.val <= 104

中文题目

给你一棵二叉树，它的根为 root 。请你删除 1 条边，使二叉树分裂成两棵子树，且它们子树和的乘积尽可能大。

由于答案可能会很大，请你将结果对 10^9 + 7 取模后再返回。

 

示例 1：

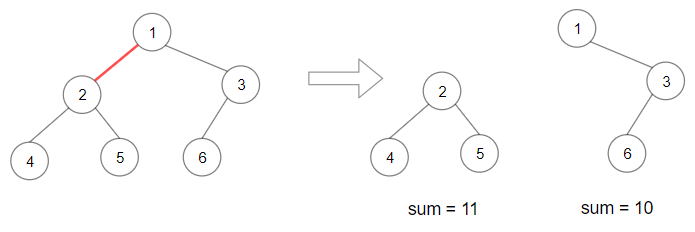
输入：root = [1,2,3,4,5,6]
输出：110
解释：删除红色的边，得到 2 棵子树，和分别为 11 和 10 。它们的乘积是 110 （11*10）

示例 2：

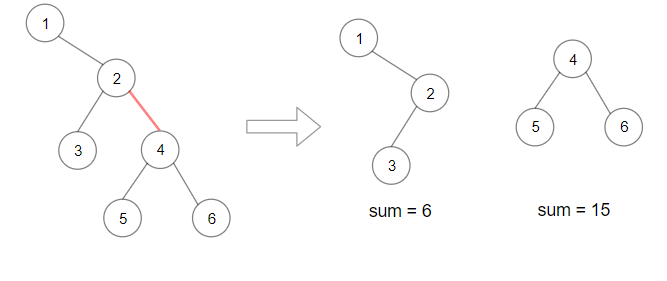
输入：root = [1,null,2,3,4,null,null,5,6]
输出：90
解释：移除红色的边，得到 2 棵子树，和分别是 15 和 6 。它们的乘积为 90 （15*6）

示例 3：

输入：root = [2,3,9,10,7,8,6,5,4,11,1]
输出：1025

示例 4：

输入：root = [1,1]
输出：1

 

提示：

• 每棵树最多有 50000 个节点，且至少有 2 个节点。
• 每个节点的值在 [1, 10000] 之间。

通过代码

高赞题解

解题思路

1. 后序遍历得到分别以各个节点为根的子树总和
2. 去掉一条边的乘积 = 子树总和 * （总和 - 子树总和），取最大值
3. 不能提前取模。比如 1e9 + 7（取模后为0） 和 1e9 + 6（取模后不变），提前取模会导致错误

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    vector<long> sums;
    static const int mod = 1e9 + 7;
    int maxProduct(TreeNode* root) {
        postOrder(root);
        long res = -1;
        for (int i = 0; i < sums.size() - 1; ++i) {
            // 取最大值时不能取模，应该用long型存结果
            res = max(res, sums[i] * (sums.back() - sums[i]));
        }
        return (int)(res % mod);
    }

    long postOrder(TreeNode* root) {
        if (root == nullptr) return 0;
        long res = root->val + postOrder(root->left) + postOrder(root->right);
        sums.push_back(res);
        return res;
    }
};

统计信息

通过次数	提交次数	AC比率
8669	21666	40.0%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言