原文链接: https://leetcode-cn.com/problems/angle-between-hands-of-a-clock

英文原文

Given two numbers, hour and minutes. Return the smaller angle (in degrees) formed between the hour and the minute hand.

 

Example 1:

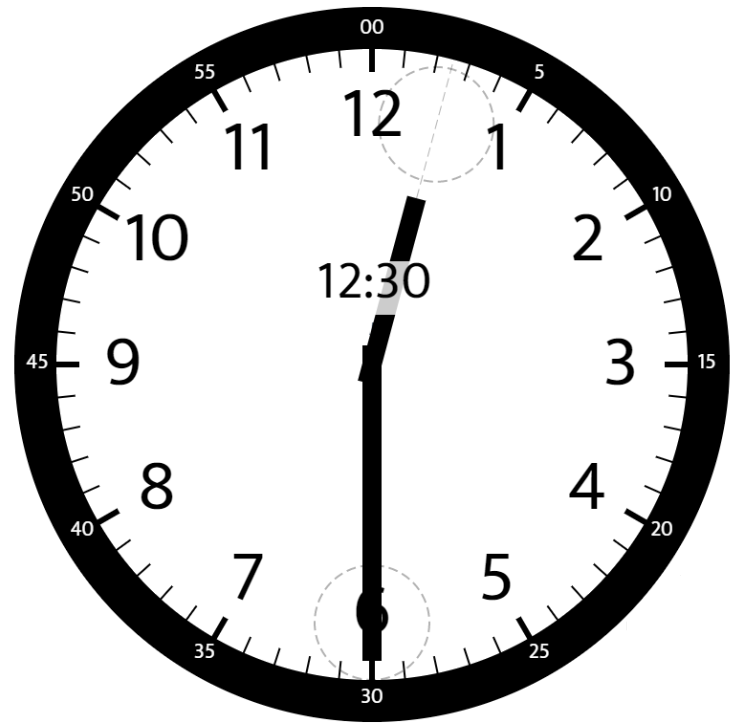
Input: hour = 12, minutes = 30
Output: 165

Example 2:

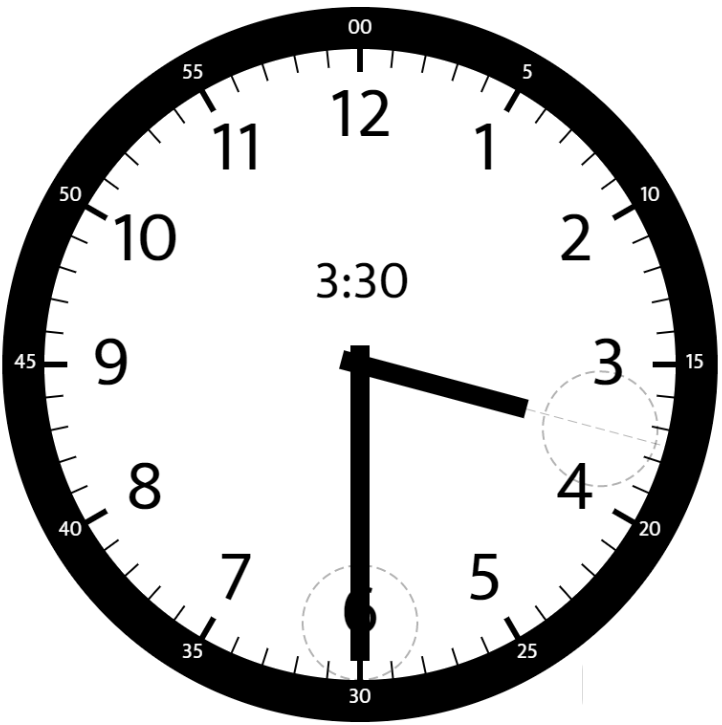
Input: hour = 3, minutes = 30
Output: 75

Example 3:

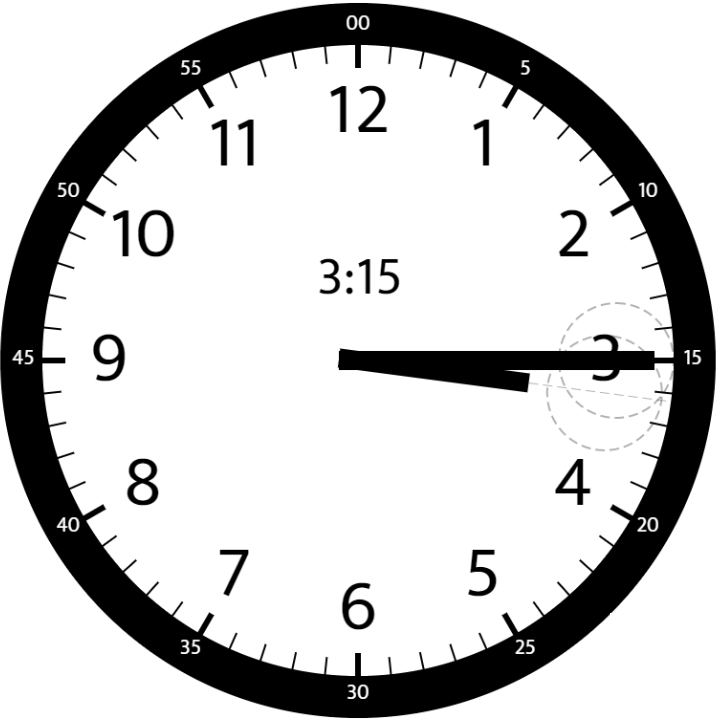
Input: hour = 3, minutes = 15
Output: 7.5

Example 4:

Input: hour = 4, minutes = 50
Output: 155

Example 5:

Input: hour = 12, minutes = 0
Output: 0

 

Constraints:

• 1 <= hour <= 12
• 0 <= minutes <= 59
• Answers within 10^-5 of the actual value will be accepted as correct.

中文题目

给你两个数 hour 和 minutes 。请你返回在时钟上，由给定时间的时针和分针组成的较小角的角度（60 单位制）。

 

示例 1：

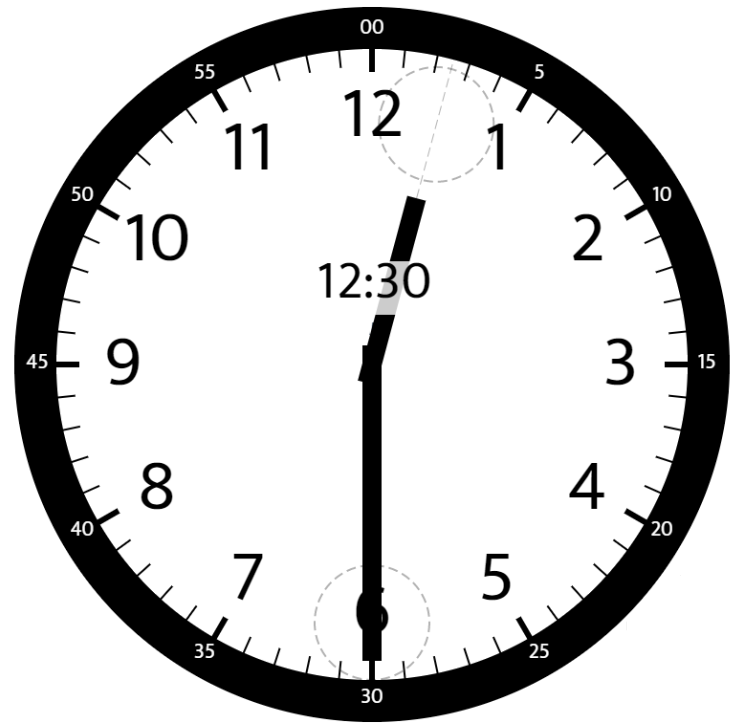
输入：hour = 12, minutes = 30
输出：165

示例 2：

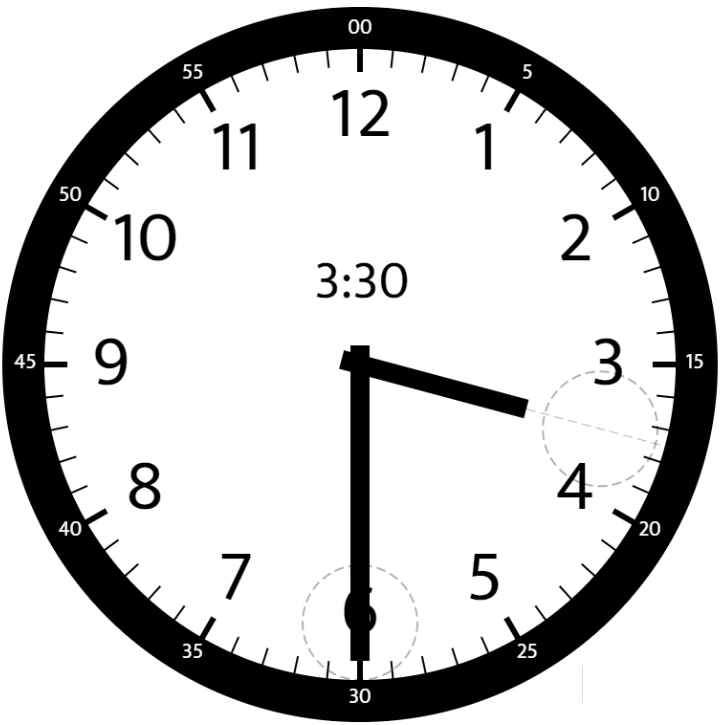
输入：hour = 3, minutes = 30
输出；75

示例 3：

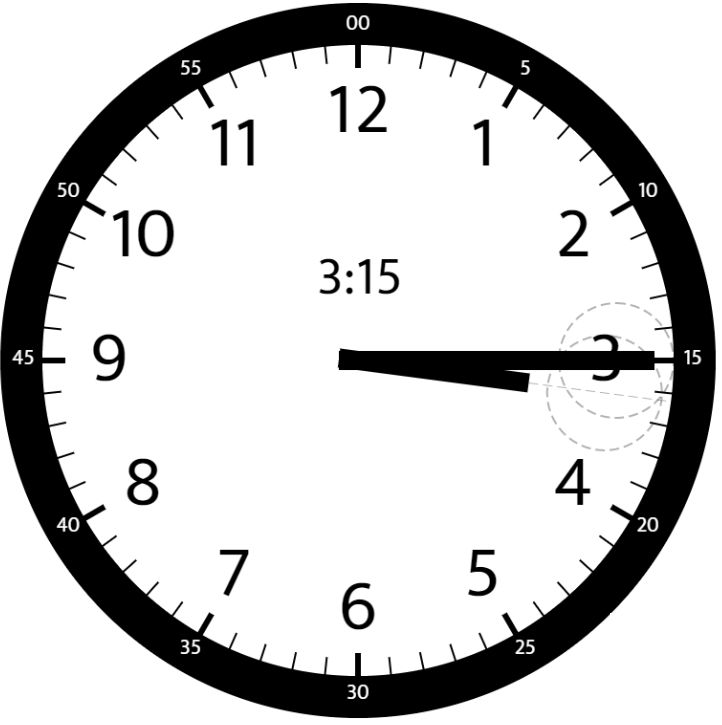
输入：hour = 3, minutes = 15
输出：7.5

示例 4：

输入：hour = 4, minutes = 50
输出：155

示例 5：

输入：hour = 12, minutes = 0
输出：0

 

提示：

• 1 <= hour <= 12
• 0 <= minutes <= 59
• 与标准答案误差在 10^-5 以内的结果都被视为正确结果。

通过代码

官方题解

方法一：数学

其思想是分别计算 0 点垂线与每个指针之间的角度。答案是这两个角度的差。

分针的角度：
我们从分针开始，整个圆 $360°$ 有 60 分钟。分针指针移动一分钟的角度是 $1 \text{ min} = 360° / 60 = 6°$。

现在可以很容易地找到 0 点垂直线和分钟指针之间的角度：$\text{minutes_angle} = \text{minutes} \times 6°$。

时针的角度：
与分针的角度相似，整个圆 $360°$ 有 12 个小时，因此每个小时 $1 \text{h} = 360° / 12 = 30°$。

则时针的角度为：$\text{hour_angle} = \text{hour} \times 30°$。

由于 12 点的角度实际为 0，则需要修改表达式为：$\text{hour_angle} = (\text{hour mod } 12) \ \times 30°$。

在分钟指针大于 0 的情况下，必须考虑到时针指针额外的移动：它不在整数值之间跳跃，是跟着分针移动。

$$
\text{hour_angle} = \left(\text{hour mod } 12 + \text{minutes} / 60 \right)\times 30°
$$

算法：

• 初始化常数：one_min_angle = 6，one_hour_angle = 30。
• 分针指针与 0 点垂线的角度为：minutes_angle = one_min_angle * minutes。
• 时针指针与 0 点垂线的角度为：hour_angle = (hour % 12 + minutes / 60) * one_hour_angle。
• 得到差：diff = abs(hour_angle - minutes_angle)。
• 返回最小的角度：min(diff, 360 - diff)。

[solution1-Python]
class Solution:
    def angleClock(self, hour: int, minutes: int) -> float:
        one_min_angle = 6
        one_hour_angle = 30
        
        minutes_angle = one_min_angle * minutes
        hour_angle = (hour % 12 + minutes / 60) * one_hour_angle
        
        diff = abs(hour_angle - minutes_angle)
        return min(diff, 360 - diff)

[solution1-Java]
class Solution {
  public double angleClock(int hour, int minutes) {
    int oneMinAngle = 6;
    int oneHourAngle = 30;

    double minutesAngle = oneMinAngle * minutes;
    double hourAngle = (hour % 12 + minutes / 60.0) * oneHourAngle;

    double diff = Math.abs(hourAngle - minutesAngle);
    return Math.min(diff, 360 - diff);
  }
}

[solution1-C++]
class Solution {
  public:
  double angleClock(int hour, int minutes) {
    int oneMinAngle = 6;
    int oneHourAngle = 30;

    double minutesAngle = oneMinAngle * minutes;
    double hourAngle = (hour % 12 + minutes / 60.0) * oneHourAngle;

    double diff = abs(hourAngle - minutesAngle);
    return min(diff, 360 - diff);
  }
};

[solution1-Go]
func angleClock(hour int, minutes int) float64 {
    var oneMinAngle, oneHourAngle, minutesAngle, hourAngle, diff float64;
    oneMinAngle = 6;
    oneHourAngle = 30;

    minutesAngle = oneMinAngle * float64(minutes);
    hourAngle = (float64(hour % 12) + float64(minutes) / 60.0) * oneHourAngle;

    diff = math.Abs(hourAngle - minutesAngle);
    return math.Min(diff, 360 - diff);
}

复杂度分析

• 时间复杂度：$\mathcal{O}(1)$。
• 空间复杂度：$\mathcal{O}(1)$。

统计信息

通过次数	提交次数	AC比率
6460	10852	59.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言