原文链接: https://leetcode-cn.com/problems/maximum-number-of-events-that-can-be-attended

英文原文

Given an array of events where events[i] = [startDayi, endDayi]. Every event i starts at startDayi and ends at endDayi.

You can attend an event i at any day d where startTimei <= d <= endTimei. Notice that you can only attend one event at any time d.

Return the maximum number of events you can attend.

 

Example 1:

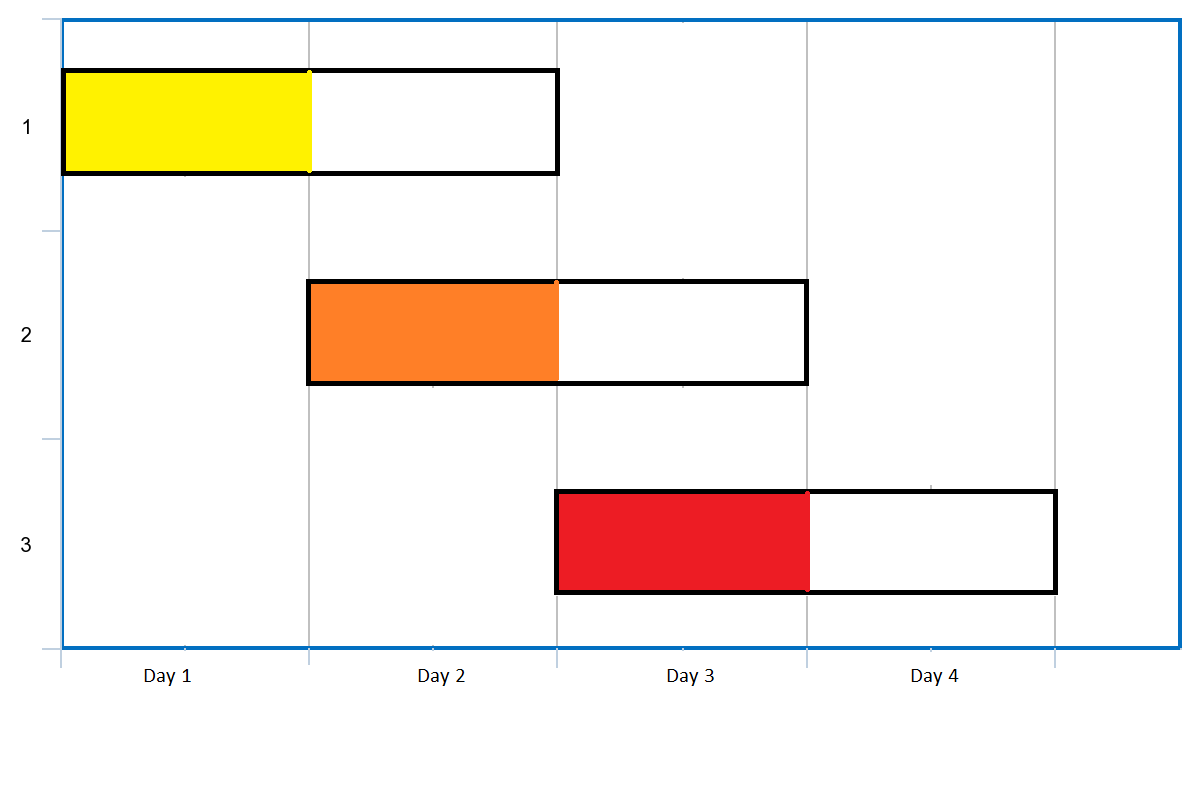
Input: events = [[1,2],[2,3],[3,4]]
Output: 3
Explanation: You can attend all the three events.
One way to attend them all is as shown.
Attend the first event on day 1.
Attend the second event on day 2.
Attend the third event on day 3.

Example 2:

Input: events= [[1,2],[2,3],[3,4],[1,2]]
Output: 4

Example 3:

Input: events = [[1,4],[4,4],[2,2],[3,4],[1,1]]
Output: 4

Example 4:

Input: events = [[1,100000]]
Output: 1

Example 5:

Input: events = [[1,1],[1,2],[1,3],[1,4],[1,5],[1,6],[1,7]]
Output: 7

 

Constraints:

• 1 <= events.length <= 105
• events[i].length == 2
• 1 <= startDayi <= endDayi <= 105

中文题目

给你一个数组 events，其中 events[i] = [startDayi, endDayi] ，表示会议 i 开始于 startDayi ，结束于 endDayi 。

你可以在满足 startDayi <= d <= endDayi 中的任意一天 d 参加会议 i 。注意，一天只能参加一个会议。

请你返回你可以参加的 最大 会议数目。

 

示例 1：

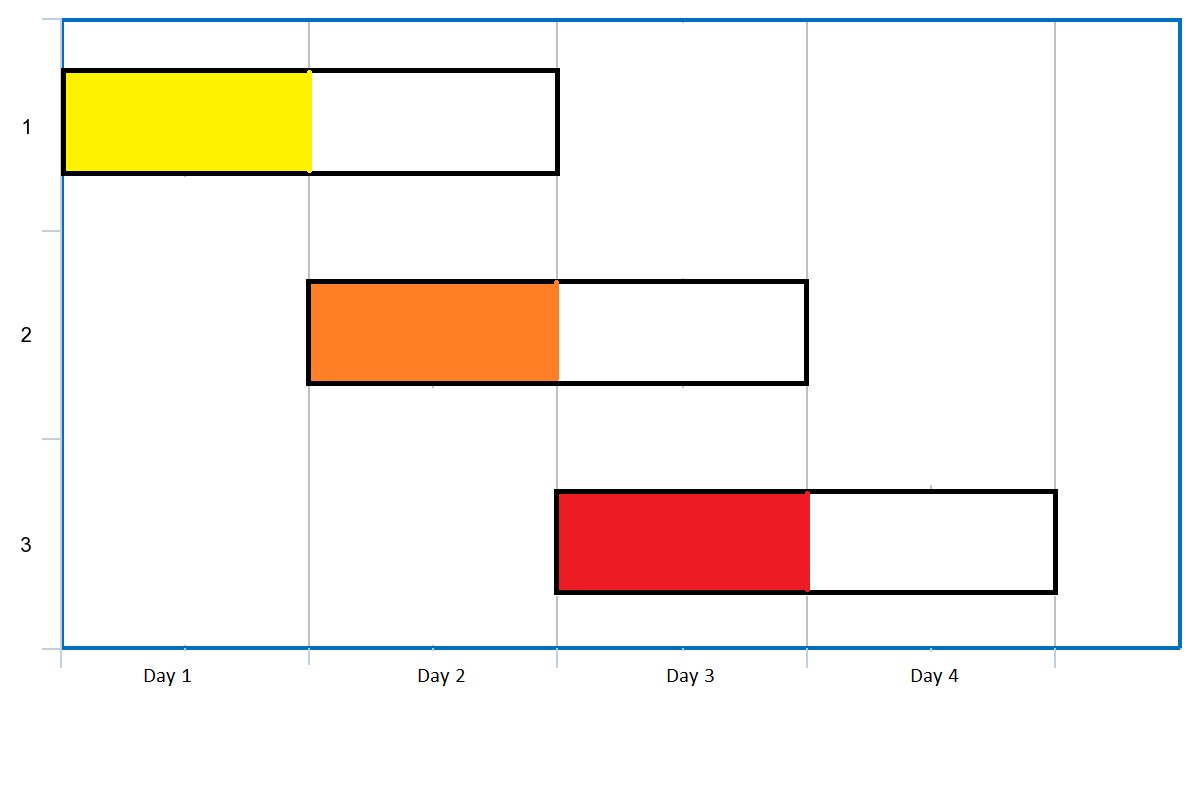
输入：events = [[1,2],[2,3],[3,4]]
输出：3
解释：你可以参加所有的三个会议。
安排会议的一种方案如上图。
第 1 天参加第一个会议。
第 2 天参加第二个会议。
第 3 天参加第三个会议。

示例 2：

输入：events= [[1,2],[2,3],[3,4],[1,2]]
输出：4

示例 3：

输入：events = [[1,4],[4,4],[2,2],[3,4],[1,1]]
输出：4

示例 4：

输入：events = [[1,100000]]
输出：1

示例 5：

输入：events = [[1,1],[1,2],[1,3],[1,4],[1,5],[1,6],[1,7]]
输出：7

 

提示：

• 1 <= events.length <= 10^5
• events[i].length == 2
• 1 <= events[i][0] <= events[i][1] <= 10^5

通过代码

高赞题解

这是一道典型的扫描算法题。由于每个时间点最多参加一个会议，我们可以从1开始遍历所有时间。

对于每一个时间点，所有在当前时间及之前时间开始，并且在当前时间还未结束的会议都是可参加的。显然，在所有可参加的会议中，选择结束时间最早的会议是最优的，因为其他会议还有更多的机会可以去参加。

怎样动态获得当前结束时间最早的会议呢？我们可以使用一个小根堆记录所有当前可参加会议的结束时间。在每一个时间点，我们首先将当前时间点开始的会议加入小根堆，再把当前已经结束的会议移除出小根堆（因为已经无法参加了），然后从剩下的会议中选择一个结束时间最早的去参加。

为了快速获得当前时间点开始的会议，我们以$O(N)$时间预处理得到每个时间点开始的会议的序号。

算法总的时间复杂度为$O(T\log N)$（这里的$T$为时间范围）。

参考代码

const int MAX = 1e5 + 1;

class Solution {
public:
    int maxEvents(vector<vector<int>>& events) {
        vector<vector<int>> left(MAX);
        for (int i = 0; i < events.size(); ++i)
            left[events[i][0]].emplace_back(i);
        
        int ans = 0;
        priority_queue<int, vector<int>, greater<>> pq;
        for (int i = 1; i < MAX; ++i) {
            for (int j : left[i])
                pq.push(events[j][1]);
            while (!pq.empty() && pq.top() < i)
                pq.pop();
            if (!pq.empty()) {
                pq.pop();
                ans++;
            }
        }
        return ans;
    }
};

统计信息

通过次数	提交次数	AC比率
12101	42248	28.6%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言