原文链接: https://leetcode-cn.com/problems/validate-binary-tree-nodes

英文原文

You have n binary tree nodes numbered from 0 to n - 1 where node i has two children leftChild[i] and rightChild[i], return true if and only if all the given nodes form exactly one valid binary tree.

If node i has no left child then leftChild[i] will equal -1, similarly for the right child.

Note that the nodes have no values and that we only use the node numbers in this problem.

 

Example 1:

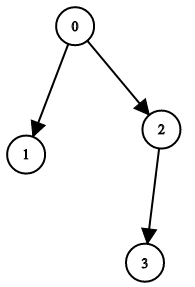
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
Output: true

Example 2:

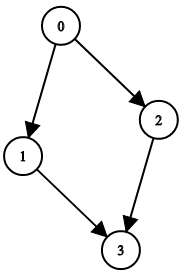
Input: n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
Output: false

Example 3:

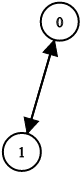
Input: n = 2, leftChild = [1,0], rightChild = [-1,-1]
Output: false

Example 4:

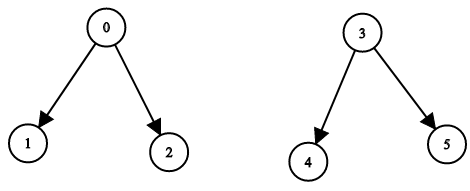
Input: n = 6, leftChild = [1,-1,-1,4,-1,-1], rightChild = [2,-1,-1,5,-1,-1]
Output: false

 

Constraints:

• 1 <= n <= 104
• leftChild.length == rightChild.length == n
• -1 <= leftChild[i], rightChild[i] <= n - 1

中文题目

二叉树上有 n 个节点，按从 0 到 n - 1 编号，其中节点 i 的两个子节点分别是 leftChild[i] 和 rightChild[i]。

只有 所有 节点能够形成且 只 形成 一颗 有效的二叉树时，返回 true；否则返回 false。

如果节点 i 没有左子节点，那么 leftChild[i] 就等于 -1。右子节点也符合该规则。

注意：节点没有值，本问题中仅仅使用节点编号。

 

示例 1：

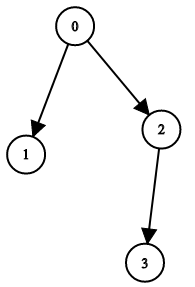
输入：n = 4, leftChild = [1,-1,3,-1], rightChild = [2,-1,-1,-1]
输出：true

示例 2：

输入：n = 4, leftChild = [1,-1,3,-1], rightChild = [2,3,-1,-1]
输出：false

示例 3：

输入：n = 2, leftChild = [1,0], rightChild = [-1,-1]
输出：false

示例 4：

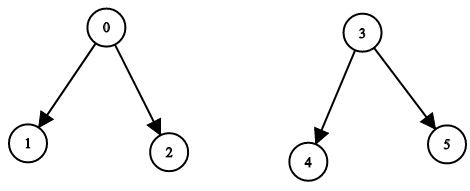
输入：n = 6, leftChild = [1,-1,-1,4,-1,-1], rightChild = [2,-1,-1,5,-1,-1]
输出：false

 

提示：

• 1 <= n <= 10^4
• leftChild.length == rightChild.length == n
• -1 <= leftChild[i], rightChild[i] <= n - 1

通过代码

高赞题解

解题思路：

• 首先我们思考什么是树，树就是无环的连通图！怎么检测是否存在环和计算连通分支数？当然是用并查集啦！
• 除了检测环和连通分支数，我们还需要进行一些特殊的判断，例如一个孩子存在多个父亲，一个父亲的存在两个相同的孩子。
• 各位力扣老爷，公审天皇，传播自由花费巨大，还请各位立刻捐赠20个赞，以便我军再战。

  class Solution {
      // 并查集用的集合列表
      List<Integer> p = new ArrayList<>();
      // 用于统计不相交的连通分支个数
      int cnt;
      public boolean validateBinaryTreeNodes(int n, int[] leftChild, int[] rightChild) {
          // 用于标记各个孩子的父节点
          int[] father = new int[n];
          // 初始化
          Arrays.fill(father, -1);
          // 初始化并查集集合状态
          for(int i = 0; i < n; i++) p.add(i);
          // 初始化分支数
          cnt = n;
          // 遍历所有节点
          for(int i = 0; i < n; i++) {
              // 如果节点存在两个孩子，而且两个孩子相同，那么显然是错误的二叉树
              if(leftChild[i] == rightChild[i] && leftChild[i] != -1) return false;
              // 合并两个孩子
              if(!merge(father, i, leftChild[i]) || !merge(father, i, rightChild[i])) return false;
          }
  
          // 如果最后所有的节点组成一个连通分支，才是一棵树
          if(cnt == 1) return true;
          return false;
  
      }
      // 和并父亲和孩子节点，并判断逻辑
      private boolean merge(int[] father, int f, int c) {
          // 孩子是空的，直接返回
          if(c == -1) return true;
          // 孩子之前有爸爸了，就是错的
          if(father[c] != -1) return false;
          // 并查集查找两个集合的根
          int a = find(f), b = find(c);
          // 如果孩子和父亲已经存在于一个集合中，那么说明会产生环，返回错误
          if(a == b) return false;
          // 合并两个集合
          p.set(a, b);
          // 标记孩子的父亲是谁
          father[c] = f;
          // 连通分支数减一
          cnt --;
          return true;
      }
      // 并查集通用方法，找集合的根元素
      private int find(int x) {
          if(p.get(x) != x) {
              p.set(x, find(p.get(x)));
          }
          return p.get(x);
      }
  }

统计信息

通过次数	提交次数	AC比率
7918	19742	40.1%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言