1382-将二叉搜索树变平衡(Balance a Binary Search Tree)

原文链接: https://leetcode-cn.com/problems/balance-a-binary-search-tree

英文原文

Given the root of a binary search tree, return a balanced binary search tree with the same node values. If there is more than one answer, return any of them.

A binary search tree is balanced if the depth of the two subtrees of every node never differs by more than 1.

Example 1:

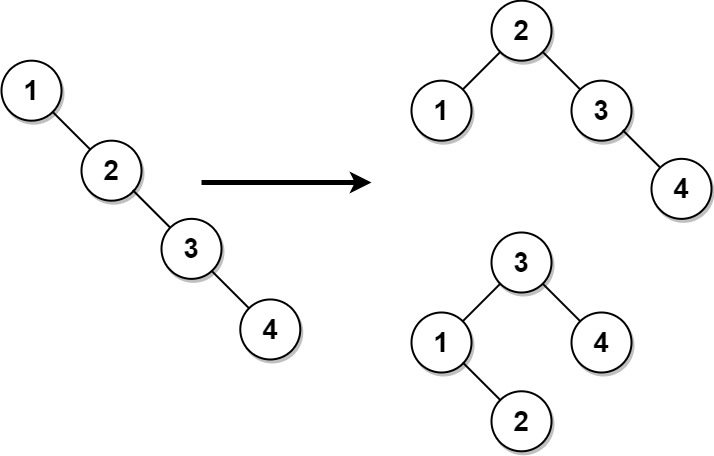
Input: root = [1,null,2,null,3,null,4,null,null]
Output: [2,1,3,null,null,null,4]
Explanation: This is not the only correct answer, [3,1,4,null,2] is also correct.

Example 2:

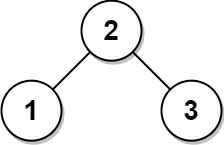
Input: root = [2,1,3]
Output: [2,1,3]

Constraints:

The number of nodes in the tree is in the range [1, 10⁴].
1 <= Node.val <= 10⁵

中文题目

给你一棵二叉搜索树，请你返回一棵 平衡后 的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。

如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是 平衡的 。

如果有多种构造方法，请你返回任意一种。

示例：

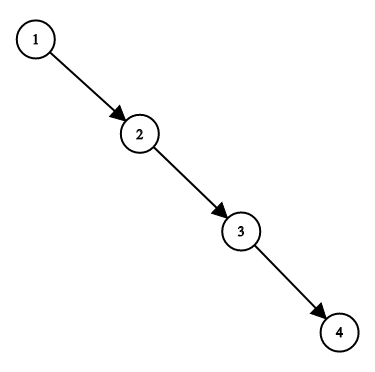
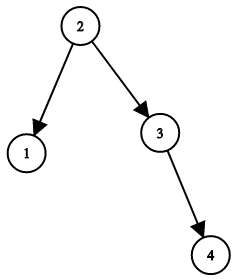
输入：root = [1,null,2,null,3,null,4,null,null]
输出：[2,1,3,null,null,null,4]
解释：这不是唯一的正确答案，[3,1,4,null,2,null,null] 也是一个可行的构造方案。

提示：

树节点的数目在 1 到 10^4 之间。
树节点的值互不相同，且在 1 到 10^5 之间。

通过代码

高赞题解

解题思路

相信看到题目后，肯定有一部分同学和我一样，认为这是要直接手撕AVL树了。这确实是一个陷阱。因为我们并没有利用到这一点：原树是一个二叉搜索树。

所以直接手撕AVL树的话，效率会偏低（但是通用性更强，一颗普通的二叉树，也可以这么玩）。

**强调，手撕AVL并不是最优解，只是通解，时间复杂度是nlog(n)**。

利用二叉搜索树的性质，中序遍历输出，然后以中间为root，递归构造树，效率更高，算是本题的最优解。

本着精益求精的指导思想，放上中序遍历构造有序数组，有序数组构造平衡二叉树的代码。手撕AVL，在这段代码之后。

public TreeNode balanceBST(TreeNode root){
        List<Integer> sortList = new ArrayList<>();
        // 中序遍历构造有序链表
        inOrder(root,sortList);
        // 有序链表构造平衡二叉树
        return buildTree(sortList,0,sortList.size()-1);
    }

    private void inOrder(TreeNode node,List<Integer> sortList){
        if (node != null){
            inOrder(node.left,sortList);
            sortList.add(node.val);
            inOrder(node.right,sortList);
        }
    }

    //有序链表构造平衡二叉树
    private TreeNode buildTree(List<Integer> sortList, int start, int end) {
        if (start > end){
            return null;
        }
        // 中间节点为root
        int mid = start + (end - start >> 1);
        TreeNode root = new TreeNode(sortList.get(mid));
        // 递归构造左右子树
        root.left = buildTree(sortList,start,mid-1);
        root.right = buildTree(sortList,mid+1,end);
        // 返回root
        return root;
    }

如果各位看官要看最优解的话，可以就此打住，下面也不浪费您的时间了

嘤嘤嘤，我不管，我就是要旋转

那好吧，我们就来手撕AVL。

如果直接在原树上调整，是非常复杂的（至少本菜鸡是这么认为的，大佬勿喷）。想想AVL树和RBT的旋转，都是在插入删除的时候进行，于是，就通过原来的二叉搜索树，重新构造一个AVL树。在插入的时候旋转。考虑的情况会少很多。

原二叉搜索树怎么遍历都行，每个节点都是新插入到AVL树中。

1.TreeNode这个结构，没有高度属性，所以我们需要一个节点高度缓存的容器，来记录每个节点的高度。
2.TreeNode没有父节点指针，所以这里采用递归的方式，进行节点的插入。

插入的过程和二叉搜索树插入过程一致，小于root，往左子树插入，大于root，往右子树插入。节点插入后，就是要根据节点的高度，动态对节点进行旋转。然后更新路径上每个节点的高度。

旋转的情况一共有4种情况：

新加入节点为 node.left 的左孩子， height(node.left) - height(node.right) > 1 。直接对node节点右旋。
新加入节点为 node.left 的右孩子， height(node.left) - height(node.right) > 1 。这时候要先对node.left左旋，调整为1的情况，再进行右旋。
新加入节点为 node.right 的右孩子， height(node.right) - height(node.left) > 1 。直接对node节点左旋。
新加入节点为 node.right 的左孩子， height(node.right) - height(node.left) > 1 。这时候要先对node.right右旋，调整为3的情况，再进行左旋。

要注意的是，节点旋转的时候，高度不是简单的+-1，而是要根据从当前节点旋转调整后的左右节点高度中获取较大值+1（本题从缓存中读取左右子树高度）。旋转高度调整完成后，返回node节点时候，也要重新计算一下新的高度，其高度为左右子树最大值+1。

旋转代码

/**
 * node节点左旋
 * @param node node
 * @param nodeHeight node高度缓存
 * @return 旋转后的当前节点
 */
private TreeNode rotateLeft(TreeNode node,Map<TreeNode,Integer> nodeHeight){
    // ---旋转进行指针调整
    TreeNode right = node.right;
    node.right = right.left;
    right.left = node;
    // ---高度更新
    // 先更新node节点的高度，这个时候node是right节点的左孩子
    int newNodeHeight = getCurNodeNewHeight(node,nodeHeight);
    // 更新node节点高度
    nodeHeight.put(node,newNodeHeight);
    // newNodeHeight是现在right节点左子树高度。
    // 原理一样，取现在right左右子树最大高度+1
    int newRightHeight = Math.max(newNodeHeight,nodeHeight.getOrDefault(right.right,0)) + 1;
    // 更新原right节点高度
    nodeHeight.put(right,newRightHeight);
    return right;
}

//获取当前节点的新高度
private int getCurNodeNewHeight(TreeNode node,Map<TreeNode,Integer> nodeHeight){
    // node节点的高度，为现在node左右子树最大高度+1
    return Math.max(nodeHeight.getOrDefault(node.left,0),nodeHeight.getOrDefault(node.right,0)) + 1;
}

节点插入后调整代码

// 往左子树插入
node.left = insert(root.left,val,nodeHeight);
// 如果左右子树高度差超过1，进行旋转调整
if (nodeHeight.getOrDefault(node.left,0) - nodeHeight.getOrDefault(node.right,0) > 1){
    if (val > node.left.val){
        // 插入在左孩子右边，左孩子先左旋
        node.left = rotateLeft(node.left,nodeHeight);
    }
    // 节点右旋
    node = rotateRight(node,nodeHeight);
}

代码

class Solution {
    public TreeNode balanceBST(TreeNode root) {
        if (root == null){
            return null;
        }
        // node节点的高度缓存
        Map<TreeNode,Integer> nodeHeight = new HashMap<>();
        TreeNode newRoot = null;
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode node = root;
        // 先序遍历插入（其实用哪个遍历都行）
        while(node != null || !stack.isEmpty()){
            if (node != null){
                // 新树插入
                newRoot = insert(newRoot,node.val,nodeHeight);
                stack.push(node);
                node = node.left;
            }else {
                node = stack.pop();
                node = node.right;
            }
        }
        return newRoot;
    }

    /**
     * 新节点插入
     * @param root root
     * @param val 新加入的值
     * @param nodeHeight 节点高度缓存
     * @return 新的root节点
     */
    private TreeNode insert(TreeNode root,int val,Map<TreeNode,Integer> nodeHeight){
        if (root == null){
            root = new TreeNode(val);
            nodeHeight.put(root,1);// 新节点的高度
            return root;
        }
        TreeNode node = root;
        int cmp = val - node.val;
        if (cmp < 0){
            // 左子树插入
            node.left = insert(root.left,val,nodeHeight);
            // 如果左右子树高度差超过1，进行旋转调整
            if (nodeHeight.getOrDefault(node.left,0) - nodeHeight.getOrDefault(node.right,0) > 1){
                if (val > node.left.val){
                    // 插入在左孩子右边，左孩子先左旋
                    node.left = rotateLeft(node.left,nodeHeight);
                }
                // 节点右旋
                node = rotateRight(node,nodeHeight);
            }
        }else if (cmp > 0){
            // 右子树插入
            node.right = insert(root.right,val,nodeHeight);
            // 如果左右子树高度差超过1，进行旋转调整
            if (nodeHeight.getOrDefault(node.right,0) - nodeHeight.getOrDefault(node.left,0) > 1){
                if (val < node.right.val){
                    // 插入在右孩子左边，右孩子先右旋
                    node.right = rotateRight(node.right,nodeHeight);
                }
                // 节点左旋
                node = rotateLeft(node,nodeHeight);
            }
        }else {
            // 一样的节点，啥都没发生
            return node;
        }
        // 获取当前节点新高度
        int height =  getCurNodeNewHeight(node,nodeHeight);
        // 更新当前节点高度
        nodeHeight.put(node,height);
        return node;
    }

    /**
     * node节点左旋
     * @param node node
     * @param nodeHeight node高度缓存
     * @return 旋转后的当前节点
     */
    private TreeNode rotateLeft(TreeNode node,Map<TreeNode,Integer> nodeHeight){
        // ---指针调整
        TreeNode right = node.right;
        node.right = right.left;
        right.left = node;
        // ---高度更新
        // 先更新node节点的高度，这个时候node是right节点的左孩子
        int newNodeHeight = getCurNodeNewHeight(node,nodeHeight);
        // 更新node节点高度
        nodeHeight.put(node,newNodeHeight);
        // newNodeHeight是现在right节点左子树高度，原理一样，取现在right左右子树最大高度+1
        int newRightHeight = Math.max(newNodeHeight,nodeHeight.getOrDefault(right.right,0)) + 1;
        // 更新原right节点高度
        nodeHeight.put(right,newRightHeight);
        return right;
    }

    /**
     * node节点右旋
     * @param node node
     * @param nodeHeight node高度缓存
     * @return 旋转后的当前节点
     */
    private TreeNode rotateRight(TreeNode node,Map<TreeNode,Integer> nodeHeight){
        // ---指针调整
        TreeNode left = node.left;
        node.left = left.right;
        left.right = node;
        // ---高度更新
        // 先更新node节点的高度，这个时候node是right节点的左孩子
        int newNodeHeight = getCurNodeNewHeight(node,nodeHeight);
        // 更新node节点高度
        nodeHeight.put(node,newNodeHeight);
        // newNodeHeight是现在left节点右子树高度，原理一样，取现在right左右子树最大高度+1
        int newLeftHeight = Math.max(newNodeHeight,nodeHeight.getOrDefault(left.left,0)) + 1;
        // 更新原left节点高度
        nodeHeight.put(left,newLeftHeight);
        return left;
    }

    /**
     * 获取当前节点的新高度
     * @param node node
     * @param nodeHeight node高度缓存
     * @return 当前node的新高度
     */
    private int getCurNodeNewHeight(TreeNode node,Map<TreeNode,Integer> nodeHeight){
        // node节点的高度，为现在node左右子树最大高度+1
        return Math.max(nodeHeight.getOrDefault(node.left,0),nodeHeight.getOrDefault(node.right,0)) + 1;
    }
}

统计信息

通过次数	提交次数	AC比率
12029	17173	70.0%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途