原文链接: https://leetcode-cn.com/problems/check-if-there-is-a-valid-path-in-a-grid

英文原文

Given a m x n grid. Each cell of the grid represents a street. The street of grid[i][j] can be:

• 1 which means a street connecting the left cell and the right cell.
• 2 which means a street connecting the upper cell and the lower cell.
• 3 which means a street connecting the left cell and the lower cell.
• 4 which means a street connecting the right cell and the lower cell.
• 5 which means a street connecting the left cell and the upper cell.
• 6 which means a street connecting the right cell and the upper cell.

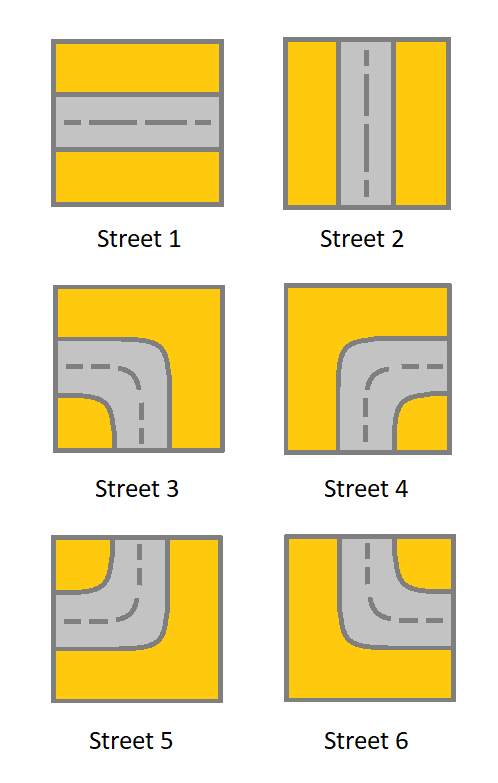
You will initially start at the street of the upper-left cell (0,0). A valid path in the grid is a path which starts from the upper left cell (0,0) and ends at the bottom-right cell (m - 1, n - 1). The path should only follow the streets.

Notice that you are not allowed to change any street.

Return true if there is a valid path in the grid or false otherwise.

 

Example 1:

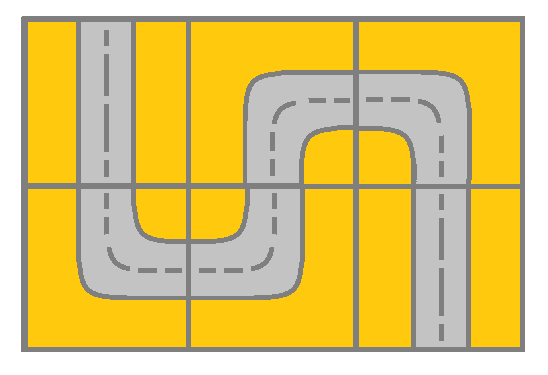
Input: grid = [[2,4,3],[6,5,2]]
Output: true
Explanation: As shown you can start at cell (0, 0) and visit all the cells of the grid to reach (m - 1, n - 1).

Example 2:

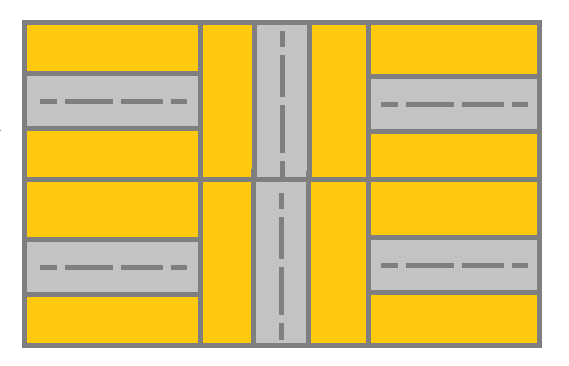
Input: grid = [[1,2,1],[1,2,1]]
Output: false
Explanation: As shown you the street at cell (0, 0) is not connected with any street of any other cell and you will get stuck at cell (0, 0)

Example 3:

Input: grid = [[1,1,2]]
Output: false
Explanation: You will get stuck at cell (0, 1) and you cannot reach cell (0, 2).

Example 4:

Input: grid = [[1,1,1,1,1,1,3]]
Output: true

Example 5:

Input: grid = [[2],[2],[2],[2],[2],[2],[6]]
Output: true

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• 1 <= grid[i][j] <= 6

中文题目

给你一个 m x n 的网格 grid。网格里的每个单元都代表一条街道。grid[i][j] 的街道可以是：

• 1 表示连接左单元格和右单元格的街道。
• 2 表示连接上单元格和下单元格的街道。
• 3 表示连接左单元格和下单元格的街道。
• 4 表示连接右单元格和下单元格的街道。
• 5 表示连接左单元格和上单元格的街道。
• 6 表示连接右单元格和上单元格的街道。

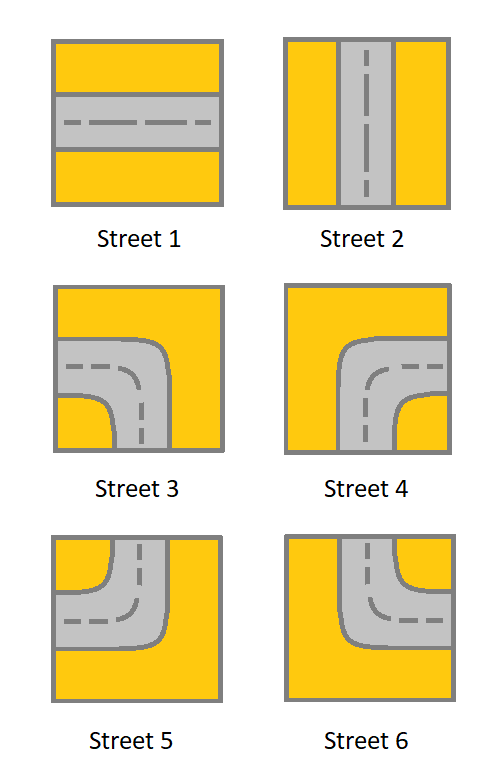
你最开始从左上角的单元格 (0,0) 开始出发，网格中的「有效路径」是指从左上方的单元格 (0,0) 开始、一直到右下方的 (m-1,n-1) 结束的路径。该路径必须只沿着街道走。

注意：你 不能 变更街道。

如果网格中存在有效的路径，则返回 true，否则返回 false 。

 

示例 1：

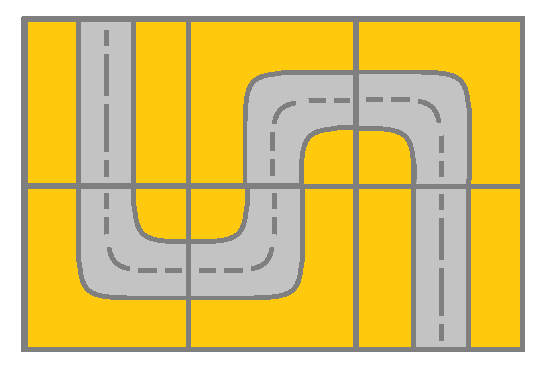
输入：grid = [[2,4,3],[6,5,2]]
输出：true
解释：如图所示，你可以从 (0, 0) 开始，访问网格中的所有单元格并到达 (m - 1, n - 1) 。

示例 2：

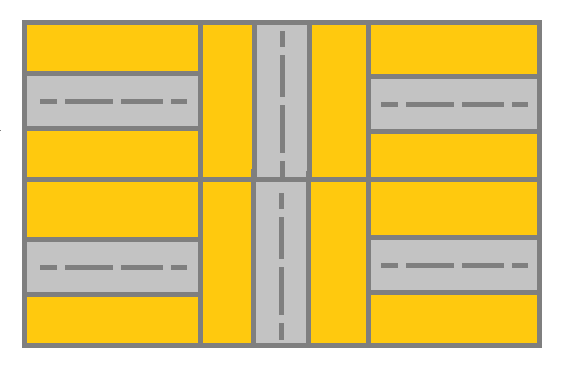
输入：grid = [[1,2,1],[1,2,1]]
输出：false
解释：如图所示，单元格 (0, 0) 上的街道没有与任何其他单元格上的街道相连，你只会停在 (0, 0) 处。

示例 3：

输入：grid = [[1,1,2]]
输出：false
解释：你会停在 (0, 1)，而且无法到达 (0, 2) 。

示例 4：

输入：grid = [[1,1,1,1,1,1,3]]
输出：true

示例 5：

输入：grid = [[2],[2],[2],[2],[2],[2],[6]]
输出：true

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• 1 <= grid[i][j] <= 6

通过代码

高赞题解

解题思路：

通过构建pipe数组，将每个拼图转化为四个方向上的移动限制图。

例：

pipe[3][2]=3，代表3号拼图可以由向上的方向进入其中，并转向左方向继续前进。

pipe[5][3]=-1，代表5号拼图不可以由向左的方向进入其中。

其中0代表向下、1代表向右、2代表向上、3代表向左、-1代表不可走

这之后问题就变成了一个简单的DFS了

class Solution {
    int m,n,dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};//0下、1右、2上、3左
    int pipe[7][4]={{-1,-1,-1,-1},{-1,1,-1,3},{0,-1,2,-1},{-1,0,3,-1},{-1,-1,1,0},{3,2,-1,-1},{1,-1,-1,2}};
    //记录各个拼图块路径的方向，0、1、2、3代表方向，-1代表不可走。
    bool dfs(int x,int y,int dir,vector<vector<int>>& grid){//(x,y,当前方向,地图)
        if(x==m-1&&y==n-1) return 1;//到达终点
        int xx=x+dx[dir];
        int yy=y+dy[dir];//得到下一个准备走的坐标
        if(xx<0||yy<0||xx>=m||yy>=n)return 0;//越界
        int nxt=grid[xx][yy];//得到下一块拼图的编号
        if(pipe[nxt][dir]!=-1)return dfs(xx,yy,pipe[nxt][dir],grid);//如果当前方向可走，则方向改变，继续走。
        return 0;//无法走，返回0
    }
    public:
    bool hasValidPath(vector<vector<int>>& grid) {    
        m=grid.size();
        n=grid[0].size();
        int sta=grid[0][0];//起点的拼图编号
        for(int i=0;i<4;++i)//朝着四个方向都试一下
            if(pipe[sta][i]!=-1)//当前方向可以走
                if(dfs(0,0,pipe[sta][i],grid))//沿着当前方向搜索
                    return 1;//拼图都有两个方向可以走，只要沿着一个初始方向走通就可以。
        return 0;
    }
};

3.23 updata

之前是加了vis数组判断是否访问过的，之后感觉没啥用，就删掉了，发现也能过题目，便没再多想。

这里很感谢@study11 @xm9304同学的质疑

同时很感谢@mapleking同学的指正。

之后，再@LeetCode加一下测试用例。

class Solution {
    int m,n,dx[4]={1,0,-1,0},dy[4]={0,1,0,-1};//0下、1右、2上、3左
    int pipe[7][4]={
        {-1,-1,-1,-1},
        {-1,1,-1,3},
        {0,-1,2,-1},
        {-1,0,3,-1},
        {-1,-1,1,0},
        {3,2,-1,-1},
        {1,-1,-1,2}
    };
    //记录各个拼图块路径的方向，0、1、2、3代表方向，-1代表不可走。
    bool vis[302][302];
    bool dfs(int x,int y,int dir,vector<vector<int>>& grid){//(x,y,当前方向,地图)
        vis[x][y]=1;
        if(x==m-1&&y==n-1) return 1;//到达终点
        int xx=x+dx[dir];
        int yy=y+dy[dir];//得到下一个准备走的坐标
        if(xx<0||yy<0||xx>=m||yy>=n)return 0;//越界
        int nxt=grid[xx][yy];//得到下一块拼图的编号
        if(pipe[nxt][dir]!=-1&&!vis[xx][yy])
            return dfs(xx,yy,pipe[nxt][dir],grid);//如果当前方向可走，则方向改变，继续走。
        return 0;//无法走，返回0
    }
    public:
    bool hasValidPath(vector<vector<int>>& grid) {    
        m=grid.size();
        n=grid[0].size();
        memset(vis,0,sizeof(vis));
        int sta=grid[0][0];//起点的拼图编号
        for(int i=0;i<4;++i)//朝着四个方向都试一下
            if(pipe[sta][i]!=-1)//当前方向可以走
                if(dfs(0,0,pipe[sta][i],grid))//沿着当前方向搜索
                    return 1;//拼图都有两个方向可以走，只要沿着一个初始方向走通就可以。
        return 0;
    }
};

统计信息

通过次数	提交次数	AC比率
6860	17077	40.2%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言