原文链接: https://leetcode-cn.com/problems/count-submatrices-with-all-ones

英文原文

Given an m x n binary matrix mat, return the number of submatrices that have all ones.

 

Example 1:

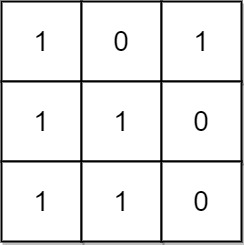
Input: mat = [[1,0,1],[1,1,0],[1,1,0]]
Output: 13
Explanation: 
There are 6 rectangles of side 1x1.
There are 2 rectangles of side 1x2.
There are 3 rectangles of side 2x1.
There is 1 rectangle of side 2x2. 
There is 1 rectangle of side 3x1.
Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.

Example 2:

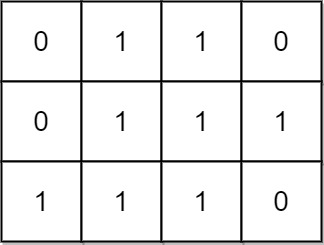
Input: mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]]
Output: 24
Explanation: 
There are 8 rectangles of side 1x1.
There are 5 rectangles of side 1x2.
There are 2 rectangles of side 1x3. 
There are 4 rectangles of side 2x1.
There are 2 rectangles of side 2x2. 
There are 2 rectangles of side 3x1. 
There is 1 rectangle of side 3x2. 
Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.

 

Constraints:

• 1 <= m, n <= 150
• mat[i][j] is either 0 or 1.

中文题目

给你一个只包含 0 和 1 的 rows * columns 矩阵 mat ，请你返回有多少个 子矩形 的元素全部都是 1 。

 

示例 1：

输入：mat = [[1,0,1],
            [1,1,0],
            [1,1,0]]
输出：13
解释：
有 6 个 1x1 的矩形。
有 2 个 1x2 的矩形。
有 3 个 2x1 的矩形。
有 1 个 2x2 的矩形。
有 1 个 3x1 的矩形。
矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。

示例 2：

输入：mat = [[0,1,1,0],
            [0,1,1,1],
            [1,1,1,0]]
输出：24
解释：
有 8 个 1x1 的子矩形。
有 5 个 1x2 的子矩形。
有 2 个 1x3 的子矩形。
有 4 个 2x1 的子矩形。
有 2 个 2x2 的子矩形。
有 2 个 3x1 的子矩形。
有 1 个 3x2 的子矩形。
矩形数目总共 = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24 。

示例 3：

输入：mat = [[1,1,1,1,1,1]]
输出：21

示例 4：

输入：mat = [[1,0,1],[0,1,0],[1,0,1]]
输出：5

 

提示：

• 1 <= rows <= 150
• 1 <= columns <= 150
• 0 <= mat[i][j] <= 1

通过代码

高赞题解

解题思路

矩阵里每个点(i.j)统计他这行左边到他这个位置最多有几个连续的1，存为left[i][j]。然后对于每个点(i.j)，我们固定子矩形的右下角为(i.j)，利用left从该行i向上寻找子矩阵左上角为第k行的矩阵个数。每次将子矩阵个数加到答案中即可。
时间复杂度O(nnm)，空间复杂度O(nm)。

代码

class Solution {
public:
    int numSubmat(vector<vector<int>>& mat) {
        int n = mat.size();
        int m = mat[0].size();
        vector<vector<int> > left(n,vector<int>(m));
        int now = 0;
        for(int i=0;i<n;i++){
            now = 0;
            for(int j=0;j<m;j++){
                if(mat[i][j] == 1) now ++;
                else now = 0;
                left[i][j] = now;
            }
        }
        int ans = 0,minx;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                minx = 0x3f3f3f3f;
                for(int k=i;k>=0;k--){
                    minx = min(left[k][j],minx);
                    ans += minx;
                }
            }
        }
        return ans;
    }
};

统计信息

通过次数	提交次数	AC比率
7790	13004	59.9%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言