1519-子树中标签相同的节点数(Number of Nodes in the Sub-Tree With the Same Label)
发表于：2021-12-03 | 分类： 中等
字数统计: 2.5k | 阅读时长: 12分钟 | 阅读量：

原文链接: https://leetcode-cn.com/problems/number-of-nodes-in-the-sub-tree-with-the-same-label

英文原文

Given a tree (i.e. a connected, undirected graph that has no cycles) consisting of n nodes numbered from 0 to n - 1 and exactly n - 1 edges. The root of the tree is the node 0, and each node of the tree has a label which is a lower-case character given in the string labels (i.e. The node with the number i has the label labels[i]).

The edges array is given on the form edges[i] = [ai, bi], which means there is an edge between nodes ai and bi in the tree.

Return an array of size n where ans[i] is the number of nodes in the subtree of the ith node which have the same label as node i.

A subtree of a tree T is the tree consisting of a node in T and all of its descendant nodes.

 

Example 1:

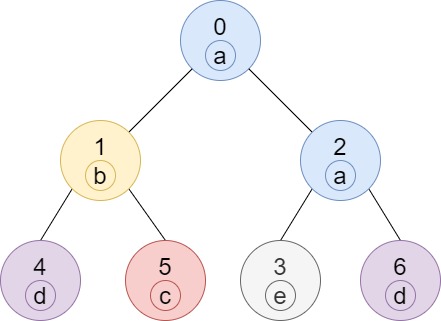
Input: n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
Output: [2,1,1,1,1,1,1]
Explanation: Node 0 has label 'a' and its sub-tree has node 2 with label 'a' as well, thus the answer is 2. Notice that any node is part of its sub-tree.
Node 1 has a label 'b'. The sub-tree of node 1 contains nodes 1,4 and 5, as nodes 4 and 5 have different labels than node 1, the answer is just 1 (the node itself).

Example 2:

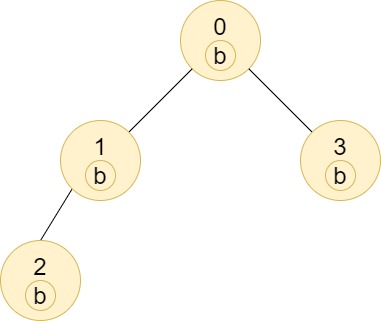
Input: n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
Output: [4,2,1,1]
Explanation: The sub-tree of node 2 contains only node 2, so the answer is 1.
The sub-tree of node 3 contains only node 3, so the answer is 1.
The sub-tree of node 1 contains nodes 1 and 2, both have label 'b', thus the answer is 2.
The sub-tree of node 0 contains nodes 0, 1, 2 and 3, all with label 'b', thus the answer is 4.

Example 3:

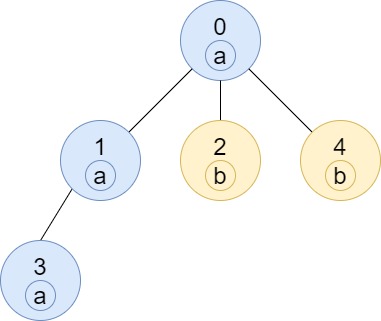
Input: n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
Output: [3,2,1,1,1]

Example 4:

Input: n = 6, edges = [[0,1],[0,2],[1,3],[3,4],[4,5]], labels = "cbabaa"
Output: [1,2,1,1,2,1]

Example 5:

Input: n = 7, edges = [[0,1],[1,2],[2,3],[3,4],[4,5],[5,6]], labels = "aaabaaa"
Output: [6,5,4,1,3,2,1]

 

Constraints:

  • 1 <= n <= 10^5
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • labels.length == n
  • labels is consisting of only of lower-case English letters.

中文题目

给你一棵树（即，一个连通的无环无向图），这棵树由编号从 0  到 n - 1 的 n 个节点组成，且恰好有 n - 1 条 edges 。树的根节点为节点 0 ，树上的每一个节点都有一个标签，也就是字符串 labels 中的一个小写字符（编号为 i 的 节点的标签就是 labels[i] ）

边数组 edges 以 edges[i] = [ai, bi] 的形式给出，该格式表示节点 ai 和 bi 之间存在一条边。

返回一个大小为 n 的数组，其中 ans[i] 表示第 i 个节点的子树中与节点 i 标签相同的节点数。

树 T 中的子树是由 T 中的某个节点及其所有后代节点组成的树。

 

示例 1：

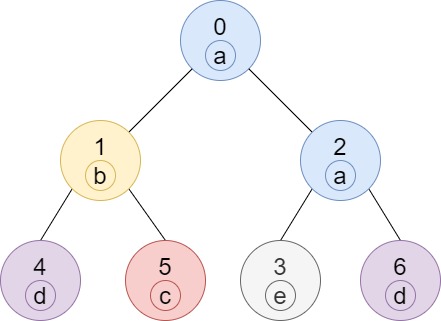
输入：n = 7, edges = [[0,1],[0,2],[1,4],[1,5],[2,3],[2,6]], labels = "abaedcd"
输出：[2,1,1,1,1,1,1]
解释：节点 0 的标签为 'a' ，以 'a' 为根节点的子树中，节点 2 的标签也是 'a' ，因此答案为 2 。注意树中的每个节点都是这棵子树的一部分。
节点 1 的标签为 'b' ，节点 1 的子树包含节点 1、4 和 5，但是节点 4、5 的标签与节点 1 不同，故而答案为 1（即，该节点本身）。

示例 2：

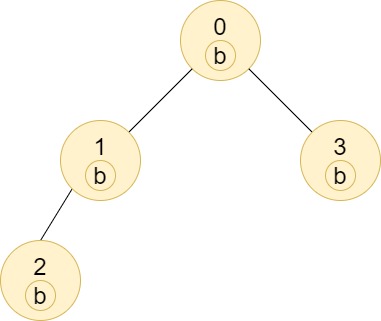
输入：n = 4, edges = [[0,1],[1,2],[0,3]], labels = "bbbb"
输出：[4,2,1,1]
解释：节点 2 的子树中只有节点 2 ，所以答案为 1 。
节点 3 的子树中只有节点 3 ，所以答案为 1 。
节点 1 的子树中包含节点 1 和 2 ，标签都是 'b' ，因此答案为 2 。
节点 0 的子树中包含节点 0、1、2 和 3，标签都是 'b'，因此答案为 4 。

示例 3：

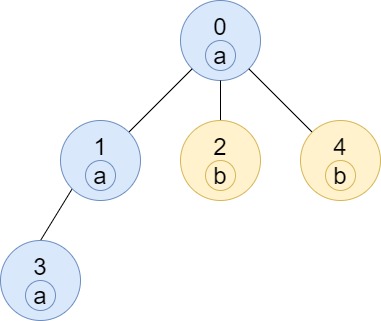
输入：n = 5, edges = [[0,1],[0,2],[1,3],[0,4]], labels = "aabab"
输出：[3,2,1,1,1]

示例 4：

输入：n = 6, edges = [[0,1],[0,2],[1,3],[3,4],[4,5]], labels = "cbabaa"
输出：[1,2,1,1,2,1]

示例 5：

输入：n = 7, edges = [[0,1],[1,2],[2,3],[3,4],[4,5],[5,6]], labels = "aaabaaa"
输出：[6,5,4,1,3,2,1]

 

提示：

  • 1 <= n <= 10^5
  • edges.length == n - 1
  • edges[i].length == 2
  • 0 <= ai, bi < n
  • ai != bi
  • labels.length == n
  • labels 仅由小写英文字母组成

通过代码

高赞题解

题目说明

给你一棵树, 但实际上一个连通的无环无向图，注意，这是一个无向图，可以看做以 0 作为根节点的树（后面有个错误，就是关于 0 是根节点这个问题）

以某个点 i 为根节点，得到 i 的子树中与 i 具有相同标签的子树个数
image.png

由于我们需要知道子树的情况，再将子树情况返回给根节点，因此我们使用后序遍历，将子树处理完，将所有的子节点的所有标签 组成数组 返回给根节点

由于只存在 26 个字母，因此我们可以使用一个 26 大小的 int 型数组存储标签

上图的 4 节点，它是叶子节点，因此它的子树加上它所有存在的标签结果是

a b c d e f g h i j k l m n o p q r s t u v w x y z
0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

将这个数组返回给 1 节点

上图的 5 节点，它是叶子节点，因此它的子树加上它所有存在的标签结果是

a b c d e f g h i j k l m n o p q r s t u v w x y z
0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

将这个数组返回给 1 节点

比如上图的 1 节点，我们接收它的子节点，即 4 和 5 返回的数组，综合它们的结果，然后加上自身标签，得到的数组就是 

a b c d e f g h i j k l m n o p q r s t u v w x y z
0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

将这个数组，返回给 1 的父节点 0

代码

class Solution {
    public int[] countSubTrees(int n, int[][] edges, String labels) {
        /*
            后序遍历
        */
        List<Integer>[] points = new List[n];
        for(int i = 0; i < n; i++){
            points[i] = new ArrayList<>();
        }
        //记录某个节点的子节点
        for(int[] p : edges){
            //单向添加，只需要知道某个节点的子节点即可
            points[p[0]].add(p[1]);
        }

        //记录每个节点对应的标签
        int[] ls = new int[n];
        for(int i = 0; i < n; i++){
            ls[i] = labels.charAt(i) - 'a';
        }

        res = new int[n];
        //0 是根节点，从 0 出发
        dfs(0, points, ls);
        return res;
    }
    int[] res;
    private int[] dfs(int i, List<Integer>[] points, int[] ls){
        int[] curLs = new int[26];
        //自身标签数 + 1
        curLs[ls[i]]++;
        for(int child : points[i]){
            int[] childLs = dfs(child, points, ls);
            for(int k = 0; k < 26; k++){
                curLs[k] += childLs[k];
            }
        }
        res[i] = curLs[ls[i]];
        //将标签结果返回给父节点
        return curLs;
    }
}

错误产生

当然，本来以为上面可以过了，不过出现了这么一个用例

输入：
4
[[0,2],[0,3],[1,2]]
"aeed"
输出：
[1,0,1,1]
预期：
[1,1,2,1]

我们可以看出，它的图形是这样的
image.png
即这样看的话， 2 存在两个父节点，0 和 1，我们上面只添加了每个节点的子节点，然后默认一个节点只有一个父节点，从 0 开始 dfs
所以导致 1 节点对应的结果为 0,因为我们没有遍历到 1

然后继续修改代码，不再只是遍历 0 号节点，而是遍历所有节点
当某个节点的结果为 0 时，表示它没有遍历过（因为如果遍历过了，那么结果至少为 1，即它本身）

for(int i = 0; i < n; i++){
    if(res[i] == 0){
        dfs(i, points, ls);
    }
}

但还是错在原来那个用例

输入：
4
[[0,2],[0,3],[1,2]]
"aeed"
输出：
[1,2,1,1]
预期：
[1,1,2,1]

这次 1 节点 和 2 节点的结果反了， 节点 2 的结果为 2， 而 节点 1 的结果为 1
这表示 2 是把 1 当作子节点的，即
image.png

因此，我们不能再单单按照 [1, 2] 的顺序将 1 当作 2 的父节点
题目说的无向图的意思就出来了，[1, 2] 不意味着 1 是 2 的父节点，而是存在一条连通的路
这里是 0 能到 2，所以我们应该从 2 出发，真正的路径是 2 -> 1
因此，我们需要进行双向添加

for(int[] p : edges){
    points[p[0]].add(p[1]);
    points[p[1]].add(p[0]);
}

使用一个 visited 数组，记录遍历过程中判断节点是否已经遍历过

最终代码

class Solution {
    public int[] countSubTrees(int n, int[][] edges, String labels) {
        /*
            后序遍历
        */
        List<Integer>[] points = new List[n];
        for(int i = 0; i < n; i++){
            points[i] = new ArrayList<>();
        }
        for(int[] p : edges){
            points[p[0]].add(p[1]);
            points[p[1]].add(p[0]);
        }

        int[] ls = new int[n];
        for(int i = 0; i < n; i++){
            ls[i] = labels.charAt(i) - 'a';
        }

        res = new int[n];
        visited = new boolean[n];
        visited[0] = true;
        dfs(0, points, ls);
        return res;
    }
    int[] res;
    boolean[] visited;
    private int[] dfs(int i, List<Integer>[] points, int[] ls){
        int[] curLs = new int[26];
        //添加自身节点
        curLs[ls[i]]++;
        for(int child : points[i]){
            /*
                判断是否已经遍历过该节点，如果遍历过，那么跳过
                因为这是无向图, 1 可以到 2，2 也可以到 1，因此，当 1 到 2 的时候，我们需要记录 1 已经访问
                这样，从 2 出发，就不会再到 1 了
            */
            if(visited[child]){
                continue;
            }
            visited[child] = true;
            int[] childLs = dfs(child, points, ls);
            for(int k = 0; k < 26; k++){
                curLs[k] += childLs[k];
            }
        }
        res[i] = curLs[ls[i]];
        return curLs;
    }
}

统计信息

通过次数 提交次数 AC比率
5628 18784 30.0%

提交历史

提交时间 提交结果 执行时间 内存消耗 语言
深度优先搜索 广度优先搜索 树
上一篇:
1518-换酒问题(Water Bottles)
下一篇:
1520-最多的不重叠子字符串(Maximum Number of Non-Overlapping Substrings)
本文目录
本文目录
    •
    本站总访问量： 次 |
    Copyright © 2020 - 2021 枫奇丶宛南 | Powered by Hexo | Theme Bamboo