原文链接: https://leetcode-cn.com/problems/minimum-swaps-to-arrange-a-binary-grid

英文原文

Given an n x n binary grid, in one step you can choose two adjacent rows of the grid and swap them.

A grid is said to be valid if all the cells above the main diagonal are zeros.

Return the minimum number of steps needed to make the grid valid, or -1 if the grid cannot be valid.

The main diagonal of a grid is the diagonal that starts at cell (1, 1) and ends at cell (n, n).

 

Example 1:

Input: grid = [[0,0,1],[1,1,0],[1,0,0]]
Output: 3

Example 2:

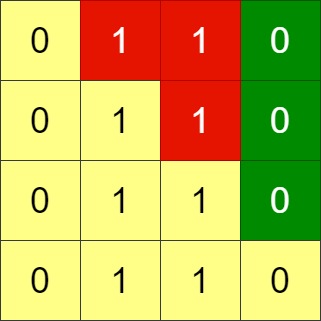
Input: grid = [[0,1,1,0],[0,1,1,0],[0,1,1,0],[0,1,1,0]]
Output: -1
Explanation: All rows are similar, swaps have no effect on the grid.

Example 3:

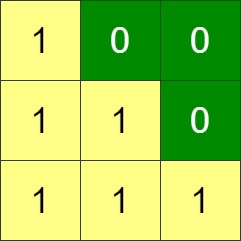
Input: grid = [[1,0,0],[1,1,0],[1,1,1]]
Output: 0

 

Constraints:

• n == grid.length == grid[i].length
• 1 <= n <= 200
• grid[i][j] is either 0 or 1

中文题目

给你一个 n x n 的二进制网格 grid，每一次操作中，你可以选择网格的 相邻两行 进行交换。

一个符合要求的网格需要满足主对角线以上的格子全部都是 0 。

请你返回使网格满足要求的最少操作次数，如果无法使网格符合要求，请你返回 -1 。

主对角线指的是从 (1, 1) 到 (n, n) 的这些格子。

 

示例 1：

输入：grid = [[0,0,1],[1,1,0],[1,0,0]]
输出：3

示例 2：

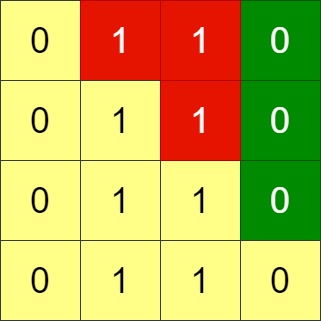
输入：grid = [[0,1,1,0],[0,1,1,0],[0,1,1,0],[0,1,1,0]]
输出：-1
解释：所有行都是一样的，交换相邻行无法使网格符合要求。

示例 3：

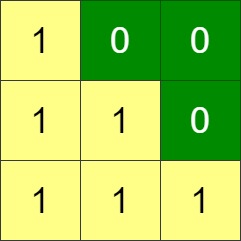
输入：grid = [[1,0,0],[1,1,0],[1,1,1]]
输出：0

 

提示：

• n == grid.length
• n == grid[i].length
• 1 <= n <= 200
• grid[i][j] 要么是 0 要么是 1 。

通过代码

高赞题解

解题思路：

这道题看似花里胡哨，转换一下类似一道排序。

要想实现对角线以上格子全是 $0$，那么我们只需要记录，每一行从后往前遍历，连续0的个数。
并且，（假设是 n x n 网格）

• 第一行是后缀 $0$必须大于等于 n - 1
• 第二行后缀 $0$ 必须大于等于 n - 2
• ……
• 0
  发现了这个规律之后，我们就可以根据贪心来找数了。

贪心的思路：

• 从第一行开始，如果该行的后缀 $0$ 满足条件，那么直接跳过进入下一行（因为需要的后缀 $0$ 个数是从大到小的顺序，所以不必担心前面的会抢后面的）
• 如果该行后缀 $0$ 个数不满足条件，那么就往下遍历找到最先（贪心，这是最小次数）满足条件的行，一行一行换上来，记录交换的次数（因为题目条件是只能相邻行之间交换，即使换的途中，中间某一行出现了符合的情况，若其上一行不满足后缀 $0$ 个数，我们还是得移动）
• 如果找不到满足条件的后缀0，那么就返回 -1。
  

  []
  class Solution {
  public:
      int minSwaps(vector<vector<int>>& grid) {
          int n = grid.size(); //网格规模
          vector<int> a; //记录每一行后缀0个数的数组
          for(int i = 0; i < n; i++)
          {
              int count = 0;
              for(int j = n - 1; j >= 0; j--)
              {
                  if(grid[i][j] == 0) count++; //数每一行的后缀0
                  else break;
              }
              a.push_back(count); 
          }
          int count = 0; //交换次数
          for(int i = 0; i < n - 1; i++)
          {
              if(a[i] >= n - i - 1) continue;//满足条件，该行直接跳过
              else{//不满足条件
                  int j = i; //用新参数遍历找满足条件的后缀0
                  for(; j < n; j++)
                  {
                      if(a[j] >= n - i - 1) break;
                  }
                  if(j == n) return -1; //找不到，直接返回-1
                  for(; j > i; j--) //找到了最先满足条件的后缀0个数 
                  {
                      swap(a[j], a[j - 1]); //每一行交换上去
                      count++; //记录交换次数
                  }
              }
          }
          return count;
      }
  };

统计信息

通过次数	提交次数	AC比率
4193	9470	44.3%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言