原文链接: https://leetcode-cn.com/problems/magnetic-force-between-two-balls
英文原文
In the universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has n empty baskets, the ith basket is at position[i], Morty has m balls and needs to distribute the balls into the baskets such that the minimum magnetic force between any two balls is maximum.
Rick stated that magnetic force between two different balls at positions x and y is |x - y|.
Given the integer array position and the integer m. Return the required force.
Example 1:
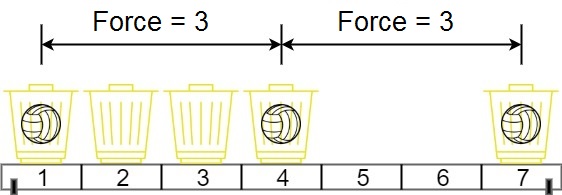
Input: position = [1,2,3,4,7], m = 3 Output: 3 Explanation: Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs [3, 3, 6]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
Example 2:
Input: position = [5,4,3,2,1,1000000000], m = 2 Output: 999999999 Explanation: We can use baskets 1 and 1000000000.
Constraints:
n == position.length2 <= n <= 1051 <= position[i] <= 109- All integers in
positionare distinct. 2 <= m <= position.length
中文题目
在代号为 C-137 的地球上,Rick 发现如果他将两个球放在他新发明的篮子里,它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子,第 i 个篮子的位置在 position[i] ,Morty 想把 m 个球放到这些篮子里,使得任意两球间 最小磁力 最大。
已知两个球如果分别位于 x 和 y ,那么它们之间的磁力为 |x - y| 。
给你一个整数数组 position 和一个整数 m ,请你返回最大化的最小磁力。
示例 1:
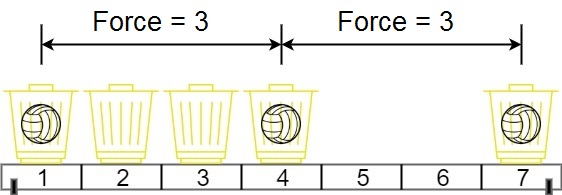
输入:position = [1,2,3,4,7], m = 3 输出:3 解释:将 3 个球分别放入位于 1,4 和 7 的三个篮子,两球间的磁力分别为 [3, 3, 6]。最小磁力为 3 。我们没办法让最小磁力大于 3 。
示例 2:
输入:position = [5,4,3,2,1,1000000000], m = 2 输出:999999999 解释:我们使用位于 1 和 1000000000 的篮子时最小磁力最大。
提示:
n == position.length2 <= n <= 10^51 <= position[i] <= 10^9- 所有
position中的整数 互不相同 。 2 <= m <= position.length
通过代码
高赞题解
思路:二分搜索
题意求最大化最小,类似这样的求最大化最小值、最小化最大值等都可以用二分搜索解决。
实现细节:
首先要找到二分搜索的边界,根据题意,要返回的是最小磁力,所以第一步要找到最小磁力的最小可能取值和最大可能取值。
对于最小可能取值,当然就是给定数组中距离最近的两个位置之间的磁力,所以对数组进行排序,并遍历数组找到相邻两个位置的最小距离。
对于最大可能取值,一共有m个球,所以有 m - 1 个间隔,最大的可能取值便是最平均的取值,所以根据给定数组最大值与最小值之差与间隔数的比值计算出平均距离,就是给定的最大可能取值。
这里给定简单证明,假设有 k 个间隔,给定数组规定的篮子间最大距离为 x,那么最小磁力的最大可能取值是 x / k,假设有某一可能取值 y 大于最大可能取值,那么所有距离都一定大于等于 y,此时假设 k 个间隔距离均为 y,总距离 ky > k * x / k = x,也大于给定的最大距离,所以不成立。
确定好了边界后,每次二分搜索时需要判断当前计算值是否满足条件,这里我们引入 check 函数,对当前计算出的最小磁力进行验证。验证过程使用贪心算法,遍历数组,若找到两位置之间距离大于等于最小磁力,则计数值加 1,最后只需要判断总计数值是否大于等于给定间隔数 m - 1 即可。
例如,示例 1 中,假设我们当前二分搜索计算出的距离为 2,那么我们遍历数组,假设第一个位置为 1,那么下一个找到的位置应该是 3,因为 3 - 1 >= 2,计数值加 1;再下面找到的是 7,因为 7 - 3 >= 2,计数值加 1。此时数组遍历完成,总计数值为 2,而给定间隔数 m - 1 = 2,满足条件,说明最小磁力为 2 是可以做到的。但如果我们当前计算出的距离为 4,那么第一个位置为 1,找到的第二个位置就只能是 7,数组遍历完成总计数值为 1,小于给定间隔数,说明最小磁力为 4 是不成立的。
在判断计算值满足条件与否之后,我们要对二分搜索边界进行转化,由于题目要求的是最大化的最小磁力,所以若当前计算出的最小磁力满足条件,我们要将左边界右移,去判断稍大一点的数值是否满足条件;若当前计算出的最小磁力不满足条件,我们要将右边界左移,判断稍小的数值是否满足条件。
由于每次满足条件后左边界右移,所以左边界的左边一个数值是一定满足条件的,所以最后返回值为 l - 1,具体返回值根据边界移动的判定规则进行判断。
代码:
[]class Solution { public: bool check(int x, vector<int>& a, int m) { int cnt = 0; int target = a[0] + x; for(int i = 0; i < a.size() - 1; i++) { if(a[i] < target && a[i + 1] >= target) { cnt++; target = a[i + 1] + x; } } return cnt >= m - 1; } int maxDistance(vector<int>& a, int m) { sort(a.begin(), a.end()); int len = a.size(); int diff = a[len - 1] - a[0]; // 最大间隔 int mn = INT_MAX; // 记录最小间隔 for(int i = 0; i < len - 1; i++) { if(mn > a[i + 1] - a[i]) { mn = a[i + 1] - a[i]; } } if(m == 2) { // 这里特判了m = 2的情况,也可以归到底下的代码中。 return diff; } else { int l = mn, r = diff / (m - 1); // 确定左右边界 while(l <= r) { // 二分搜索 int mid = (l + r) / 2; // printf("l = %d, r = %d, mid = %d\n", l, r, mid); if(check(mid, a, m)) { l = mid + 1; } else { r = mid - 1; } } return l - 1; } } };
复杂度分析:
数组排序时间复杂度 $O(NlgN)$,二分搜索复杂度为 $O(lgN)$,每次进行 check 需要遍历数组,复杂度 $O(N)$,所以二分整体复杂度也为 $O(NlgN)$,故时间复杂度为 $O(NlgN)$;
维护了几个变量,空间复杂度为 $O(1)$。
关注GTAlgorithm,专注周赛、面经题解分享,陪大家一起攻克算法难关~
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 9496 | 18522 | 51.3% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




