原文链接: https://leetcode-cn.com/problems/number-of-sets-of-k-non-overlapping-line-segments

英文原文

Given n points on a 1-D plane, where the ith point (from 0 to n-1) is at x = i, find the number of ways we can draw exactly k non-overlapping line segments such that each segment covers two or more points. The endpoints of each segment must have integral coordinates. The k line segments do not have to cover all n points, and they are allowed to share endpoints.

Return the number of ways we can draw k non-overlapping line segments. Since this number can be huge, return it modulo 109 + 7.

 

Example 1:

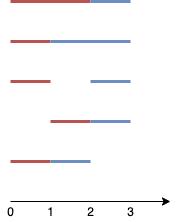
Input: n = 4, k = 2
Output: 5
Explanation: 
The two line segments are shown in red and blue.
The image above shows the 5 different ways {(0,2),(2,3)}, {(0,1),(1,3)}, {(0,1),(2,3)}, {(1,2),(2,3)}, {(0,1),(1,2)}.

Example 2:

Input: n = 3, k = 1
Output: 3
Explanation: The 3 ways are {(0,1)}, {(0,2)}, {(1,2)}.

Example 3:

Input: n = 30, k = 7
Output: 796297179
Explanation: The total number of possible ways to draw 7 line segments is 3796297200. Taking this number modulo 109 + 7 gives us 796297179.

Example 4:

Input: n = 5, k = 3
Output: 7

Example 5:

Input: n = 3, k = 2
Output: 1

 

Constraints:

• 2 <= n <= 1000
• 1 <= k <= n-1

中文题目

给你一维空间的 n 个点，其中第 i 个点（编号从 0 到 n-1）位于 x = i 处，请你找到 恰好 k 个不重叠 线段且每个线段至少覆盖两个点的方案数。线段的两个端点必须都是 整数坐标 。这 k 个线段不需要全部覆盖全部 n 个点，且它们的端点 可以 重合。

请你返回 k 个不重叠线段的方案数。由于答案可能很大，请将结果对 109 + 7 取余 后返回。

 

示例 1：

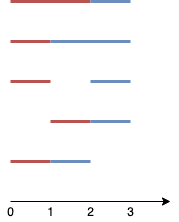
输入：n = 4, k = 2
输出：5
解释：
如图所示，两个线段分别用红色和蓝色标出。
上图展示了 5 种不同的方案 {(0,2),(2,3)}，{(0,1),(1,3)}，{(0,1),(2,3)}，{(1,2),(2,3)}，{(0,1),(1,2)} 。

示例 2：

输入：n = 3, k = 1
输出：3
解释：总共有 3 种不同的方案 {(0,1)}, {(0,2)}, {(1,2)} 。

示例 3：

输入：n = 30, k = 7
输出：796297179
解释：画 7 条线段的总方案数为 3796297200 种。将这个数对 109 + 7 取余得到 796297179 。

示例 4：

输入：n = 5, k = 3
输出：7

示例 5：

输入：n = 3, k = 2
输出：1

 

提示：

• 2 <= n <= 1000
• 1 <= k <= n-1

通过代码

高赞题解

方法一：动态规划

思路与算法

记 $f[i][j]$ 表示使用 0 .. i 的点构造了 $j$ 条线段的方案数。我们需要区分第 $j$ 条线段的右端点是否就是 $i$，因此可以考虑把 $f[i][j]$ 拆分成两个状态：

• $f[i][j][0]$ 表示第 $j$ 条线段的右端点不是 $i$，也就是说我们没有办法继续延长第 $j$ 条线段；

• $f[i][j][1]$ 表示第 $j$ 条线段的右端点就是 $i$，也就是说我们可以选择是否继续延长第 $j$ 条线段。

如何进行状态转移呢？

首先考虑 $f[i][j][0]$，因为第 $j$ 条线段的右端点不是 $i$，因此第 $i$ 个点没有用上，那么 0 .. i-1 的点构造了 $j$ 条线段，即

$$
f[i][j][0] = f[i-1][j][0] + f[i-1][j][1]
$$

再考虑 $f[i][j][1]$，因为第 $j$ 条线段的右端点就是 $i$，因此有两种情况：

• 第 $j$ 条线段长度为 $1$，那么 0 .. i-1 的点构造了 $j-1$ 条线段，即

  $$
  f[i][j][1] = f[i-1][j-1][0] + f[i-1][j-1][1]
  $$

• 第 $j$ 条线段长度大于 $1$，那么删去第 $j$ 条线段 i-1 .. i 的这一部分，0 .. i-1 的点仍然构造了 $j$ 条线段，并且点 $i-1$ 是属于第 $j$ 条线段的，即

  $$
  f[i][j][1] = f[i-1][j][1]
  $$

加上边界条件 $f[0][0][0] = 1$，最终答案即为 $f[n-1][k][0] + f[n-1][k][1]$。

注意事项

力扣对 C++ 不是很友好，编译时只开 -O1 优化，所以直接拿 vector<> 定义三维数组很容易超时。下面给出两种解决方法。

代码

第一种是定义数组，每次动态规划之前记得清空一下。

[sol11-C++]
class Solution {
private:
    static constexpr int mod = 1000000007;
    int f[1000][1001][2];

public:
    int numberOfSets(int n, int k) {
        memset(f, 0, sizeof(f));
        f[0][0][0] = 1;
        for (int i = 1; i < n; ++i) {
            for (int j = 0; j <= k; ++j) {
                f[i][j][0] = (f[i - 1][j][0] + f[i - 1][j][1]) % mod;
                f[i][j][1] = f[i - 1][j][1];
                if (j > 0) {
                    f[i][j][1] += f[i - 1][j - 1][0];
                    f[i][j][1] %= mod;
                    f[i][j][1] += f[i - 1][j - 1][1];
                    f[i][j][1] %= mod;
                }
            }
        }
        return (f[n - 1][k][0] + f[n - 1][k][1]) % mod;
    }
};

第二种是使用 vector<> 定义 pair<int, int> 的二维数组。

[sol12-C++]
class Solution {
private:
    static constexpr int mod = 1000000007;
public:
    int numberOfSets(int n, int k) {
        vector<vector<pair<int, int>>> f(n, vector<pair<int, int>>(k + 1));
        f[0][0].first = 1;
        for (int i = 1; i < n; ++i) {
            for (int j = 0; j <= k; ++j) {
                f[i][j].first = (f[i - 1][j].first + f[i - 1][j].second) % mod;
                f[i][j].second = f[i - 1][j].second;
                if (j > 0) {
                    f[i][j].second += f[i - 1][j - 1].first;
                    f[i][j].second %= mod;
                    f[i][j].second += f[i - 1][j - 1].second;
                    f[i][j].second %= mod;
                }
            }
        }
        return (f[n - 1][k].first + f[n - 1][k].second) % mod;
    }
};

复杂度分析

• 时间复杂度：$O(nk)$。

• 空间复杂度：$O(nk)$。

方法二：组合数学

思路与算法

本方法参考自某不愿透露姓名的太阳神。

题目等价于求出满足

$$
0 \leq l_1 < r_1 \leq l_2 < r_2 \leq \cdots \leq l_k < r_k < n
$$

的 $(l_1, \cdots, l_k, r_1, \cdots, r_k)$ 的数目。

令 $l’_i = l_i + (i-1)$ 以及 $r’_i = r_i + (i-1)$，$(l’_1, \cdots, l’_k, r’_1, \cdots, r’_k)$ 与 $(l_1, \cdots, l_k, r_1, \cdots, r_k)$ 逐一对应，并且满足

$$
0 \leq l’_1 < r’_1 < l’_2 < r’_2 < \cdots < l’_k < r’_k < n+k-1
$$

此时就可以使用组合求解方案数了，即在 $[0, n+k-1)$ 共 $n+k-1$ 个数中选择 $2k$ 个，因此答案为

$$
\binom{n+k-1}{2k}
$$

代码

[sol2-Python3]
class Solution:
    def numberOfSets(self, n: int, k: int) -> int:
        return math.comb(n + k - 1, k * 2) % (10**9 + 7)

复杂度分析

• 时间复杂度：用了 Python 的高精度，就当是 $O(k)$ 吧。

• 空间复杂度：$O(1)$。

统计信息

通过次数	提交次数	AC比率
1865	4226	44.1%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言