1631-最小体力消耗路径(Path With Minimum Effort)
发表于：2021-12-03 | 分类： 中等
字数统计: 644 | 阅读时长: 3分钟 | 阅读量：

原文链接: https://leetcode-cn.com/problems/path-with-minimum-effort

英文原文

You are a hiker preparing for an upcoming hike. You are given heights, a 2D array of size rows x columns, where heights[row][col] represents the height of cell (row, col). You are situated in the top-left cell, (0, 0), and you hope to travel to the bottom-right cell, (rows-1, columns-1) (i.e., 0-indexed). You can move up, down, left, or right, and you wish to find a route that requires the minimum effort.

A route's effort is the maximum absolute difference in heights between two consecutive cells of the route.

Return the minimum effort required to travel from the top-left cell to the bottom-right cell.

 

Example 1:

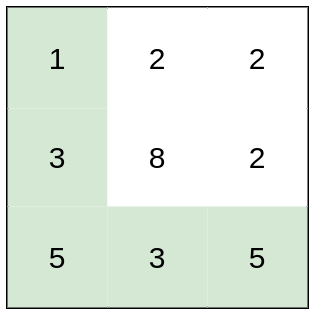
Input: heights = [[1,2,2],[3,8,2],[5,3,5]]
Output: 2
Explanation: The route of [1,3,5,3,5] has a maximum absolute difference of 2 in consecutive cells.
This is better than the route of [1,2,2,2,5], where the maximum absolute difference is 3.

Example 2:

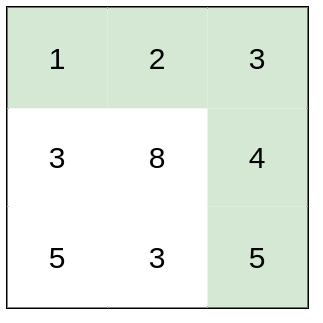
Input: heights = [[1,2,3],[3,8,4],[5,3,5]]
Output: 1
Explanation: The route of [1,2,3,4,5] has a maximum absolute difference of 1 in consecutive cells, which is better than route [1,3,5,3,5].

Example 3:

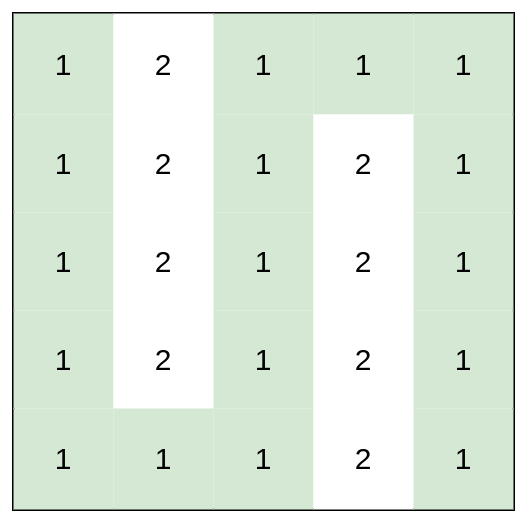
Input: heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
Output: 0
Explanation: This route does not require any effort.

 

Constraints:

  • rows == heights.length
  • columns == heights[i].length
  • 1 <= rows, columns <= 100
  • 1 <= heights[i][j] <= 106

中文题目

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往 上，下，左，右 四个方向之一移动，你想要找到耗费 体力 最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

 

示例 1：

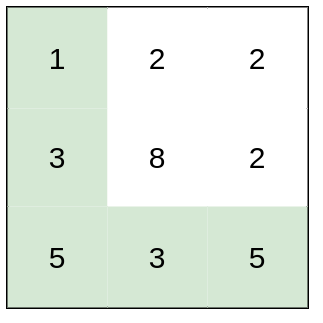
输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

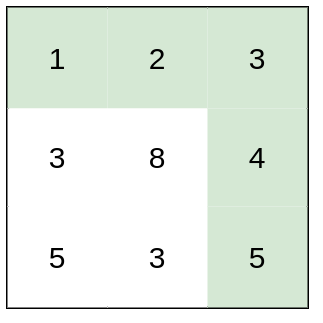
输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

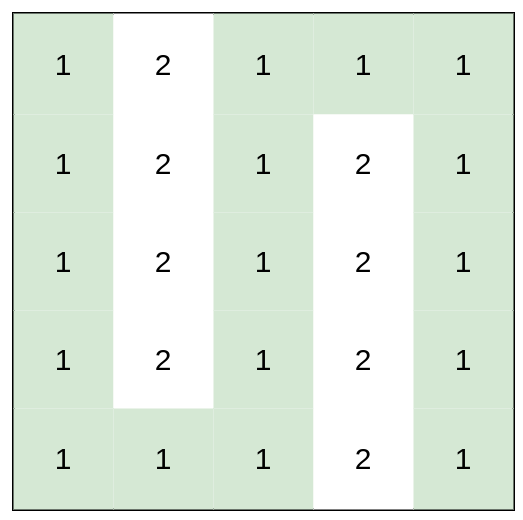
输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

 

提示：

  • rows == heights.length
  • columns == heights[i].length
  • 1 <= rows, columns <= 100
  • 1 <= heights[i][j] <= 106

通过代码

高赞题解

前言

本题实际上即为：

  • 将每个格子抽象成图中的一个点；

  • 将每两个相邻的格子之间连接一条边，长度为这两个格子本身权值的差的绝对值；

  • 需要找到一条从左上角到右下角的「最短路径」，其中路径的长度定义为路径上所有边的权值的最大值。

这也是一道比较经典的题目了，常用的方法有如下几种：

  • 「二分答案」：我们可以对最短路径的长度进行二分。当我们二分枚举到的长度为 $x$ 时，我们只保留所有长度 $\leq x$ 的边。随后从左上角开始进行搜索（深度优先搜索、广度优先搜索）均可，只需要判断是否能够到达右下角即可。

    如果能够到达右下角，我们就可以减小 $x$ 的值，反之增大 $x$ 的值。

  • 「并查集」：我们可以将所有边按照长度进行排序并依次添加进并查集，直到左上角和右下角连通为止。

  • 「最短路」：我们可以使用任一单源最短路径的算法（例如 Dijkstra 算法），只需要在维护当前路径长度时，将其修改为题目中的定义即可。

方法一：二分答案

[sol1-C++]
class Solution {
private:
    static constexpr int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
        int m = heights.size();
        int n = heights[0].size();
        int left = 0, right = 999999, ans = 0;
        while (left <= right) {
            int mid = (left + right) / 2;
            queue<pair<int, int>> q;
            q.emplace(0, 0);
            vector<int> seen(m * n);
            seen[0] = 1;
            while (!q.empty()) {
                auto [x, y] = q.front();
                q.pop();
                for (int i = 0; i < 4; ++i) {
                    int nx = x + dirs[i][0];
                    int ny = y + dirs[i][1];
                    if (nx >= 0 && nx < m && ny >= 0 && ny < n && !seen[nx * n + ny] && abs(heights[x][y] - heights[nx][ny]) <= mid) {
                        q.emplace(nx, ny);
                        seen[nx * n + ny] = 1;
                    }
                }
            }
            if (seen[m * n - 1]) {
                ans = mid;
                right = mid - 1;
            }
            else {
                left = mid + 1;
            }
        }
        return ans;
    }
};

方法二：并查集

[sol2-C++]
class UF {
public:
    vector<int> fa;
    vector<int> sz;
    int n;
    int comp_cnt;
    
public:
    UF(int _n): n(_n), comp_cnt(_n), fa(_n), sz(_n, 1) {
        iota(fa.begin(), fa.end(), 0);
    }
    
    int findset(int x) {
        return fa[x] == x ? x : fa[x] = findset(fa[x]);
    }
    
    void unite(int x, int y) {
        x = findset(x);
        y = findset(y);
        if (x == y) {
            return;
        }
        if (sz[x] < sz[y]) {
            swap(x, y);
        }
        fa[y] = x;
        sz[x] += sz[y];
        --comp_cnt;
    }
    
    bool connected(int x, int y) {
        x = findset(x);
        y = findset(y);
        return x == y;
    }
};

struct Edge {
    int x, y, z;
    Edge(int _x, int _y, int _z): x(_x), y(_y), z(_z) {}
    bool operator< (const Edge& that) const {
        return z < that.z;
    }
};

class Solution {
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
        int m = heights.size();
        int n = heights[0].size();
        vector<Edge> edges;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                int id = i * n + j;
                if (i > 0) {
                    edges.emplace_back(id - n, id, abs(heights[i][j] - heights[i - 1][j]));
                }
                if (j > 0) {
                    edges.emplace_back(id - 1, id, abs(heights[i][j] - heights[i][j - 1]));
                }
            }
        }
        
        sort(edges.begin(), edges.end());
        UF uf(m * n);
        for (const auto& edge: edges) {
            uf.unite(edge.x, edge.y);
            if (uf.connected(0, m * n - 1)) {
                return edge.z;
            }
        }
        return 0;
    }
};

方法三：最短路

[sol3-C++]
struct Dist {
    int x, y, z;
    Dist(int _x, int _y, int _z): x(_x), y(_y), z(_z) {}
    bool operator< (const Dist& that) const {
        return z > that.z;
    }
};

class Solution {
private:
    static constexpr int dirs[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    
public:
    int minimumEffortPath(vector<vector<int>>& heights) {
        int m = heights.size();
        int n = heights[0].size();
        
        priority_queue<Dist> q;
        vector<int> seen(m * n);
        vector<int> dist(m * n, INT_MAX);
        q.emplace(0, 0, 0);
        dist[0] = 0;
        while (!q.empty()) {
            auto [x, y, z] = q.top();
            q.pop();
            if (seen[x * n + y]) {
                continue;
            }
            seen[x * n + y] = 1;
            dist[x * n + y] = z;
            for (int i = 0; i < 4; ++i) {
                int nx = x + dirs[i][0];
                int ny = y + dirs[i][1];
                if (nx >= 0 && nx < m && ny >= 0 && ny < n && !seen[nx * n + ny]) {
                    q.emplace(nx, ny, max(z, abs(heights[x][y] - heights[nx][ny])));
                }
            }
        }
        return dist[m * n - 1];
    }
};

统计信息

通过次数 提交次数 AC比率
26710 54067 49.4%

提交历史

提交时间 提交结果 执行时间 内存消耗 语言
数组 深度优先搜索 广度优先搜索 二分查找 矩阵 堆（优先队列） 并查集
上一篇:
1630-等差子数组(Arithmetic Subarrays)
下一篇:
1652-拆炸弹(Defuse the Bomb)
本文目录
本文目录
    •
    本站总访问量： 次 |
    Copyright © 2020 - 2021 枫奇丶宛南 | Powered by Hexo | Theme Bamboo