原文链接: https://leetcode-cn.com/problems/where-will-the-ball-fall

英文原文

You have a 2-D grid of size m x n representing a box, and you have n balls. The box is open on the top and bottom sides.

Each cell in the box has a diagonal board spanning two corners of the cell that can redirect a ball to the right or to the left.

• A board that redirects the ball to the right spans the top-left corner to the bottom-right corner and is represented in the grid as 1.
• A board that redirects the ball to the left spans the top-right corner to the bottom-left corner and is represented in the grid as -1.

We drop one ball at the top of each column of the box. Each ball can get stuck in the box or fall out of the bottom. A ball gets stuck if it hits a "V" shaped pattern between two boards or if a board redirects the ball into either wall of the box.

Return an array answer of size n where answer[i] is the column that the ball falls out of at the bottom after dropping the ball from the ith column at the top, or -1 if the ball gets stuck in the box.

 

Example 1:

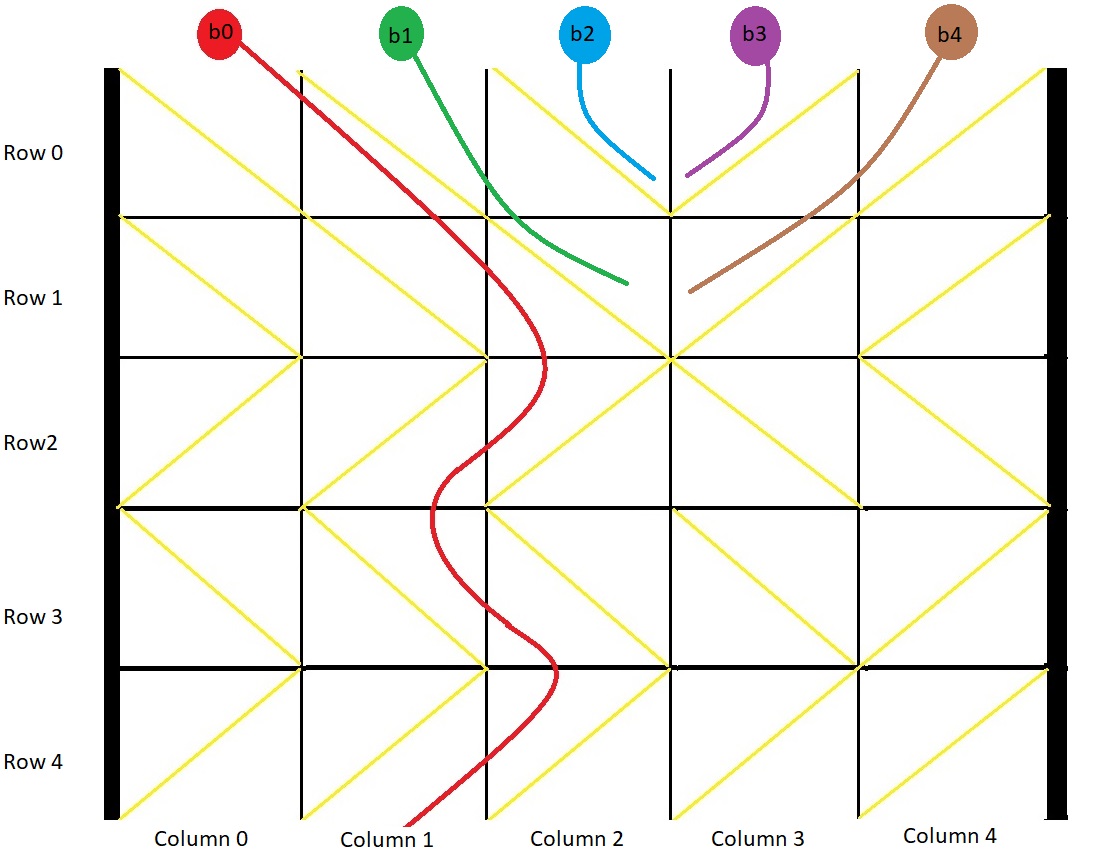
Input: grid = [[1,1,1,-1,-1],[1,1,1,-1,-1],[-1,-1,-1,1,1],[1,1,1,1,-1],[-1,-1,-1,-1,-1]]
Output: [1,-1,-1,-1,-1]
Explanation: This example is shown in the photo.
Ball b0 is dropped at column 0 and falls out of the box at column 1.
Ball b1 is dropped at column 1 and will get stuck in the box between column 2 and 3 and row 1.
Ball b2 is dropped at column 2 and will get stuck on the box between column 2 and 3 and row 0.
Ball b3 is dropped at column 3 and will get stuck on the box between column 2 and 3 and row 0.
Ball b4 is dropped at column 4 and will get stuck on the box between column 2 and 3 and row 1.

Example 2:

Input: grid = [[-1]]
Output: [-1]
Explanation: The ball gets stuck against the left wall.

Example 3:

Input: grid = [[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1],[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1]]
Output: [0,1,2,3,4,-1]

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100
• grid[i][j] is 1 or -1.

中文题目

用一个大小为 m x n 的二维网格 grid 表示一个箱子。你有 n 颗球。箱子的顶部和底部都是开着的。

箱子中的每个单元格都有一个对角线挡板，跨过单元格的两个角，可以将球导向左侧或者右侧。

• 将球导向右侧的挡板跨过左上角和右下角，在网格中用 1 表示。
• 将球导向左侧的挡板跨过右上角和左下角，在网格中用 -1 表示。

在箱子每一列的顶端各放一颗球。每颗球都可能卡在箱子里或从底部掉出来。如果球恰好卡在两块挡板之间的 "V" 形图案，或者被一块挡导向到箱子的任意一侧边上，就会卡住。

返回一个大小为 n 的数组 answer ，其中 answer[i] 是球放在顶部的第 i 列后从底部掉出来的那一列对应的下标，如果球卡在盒子里，则返回 -1 。

 

示例 1：

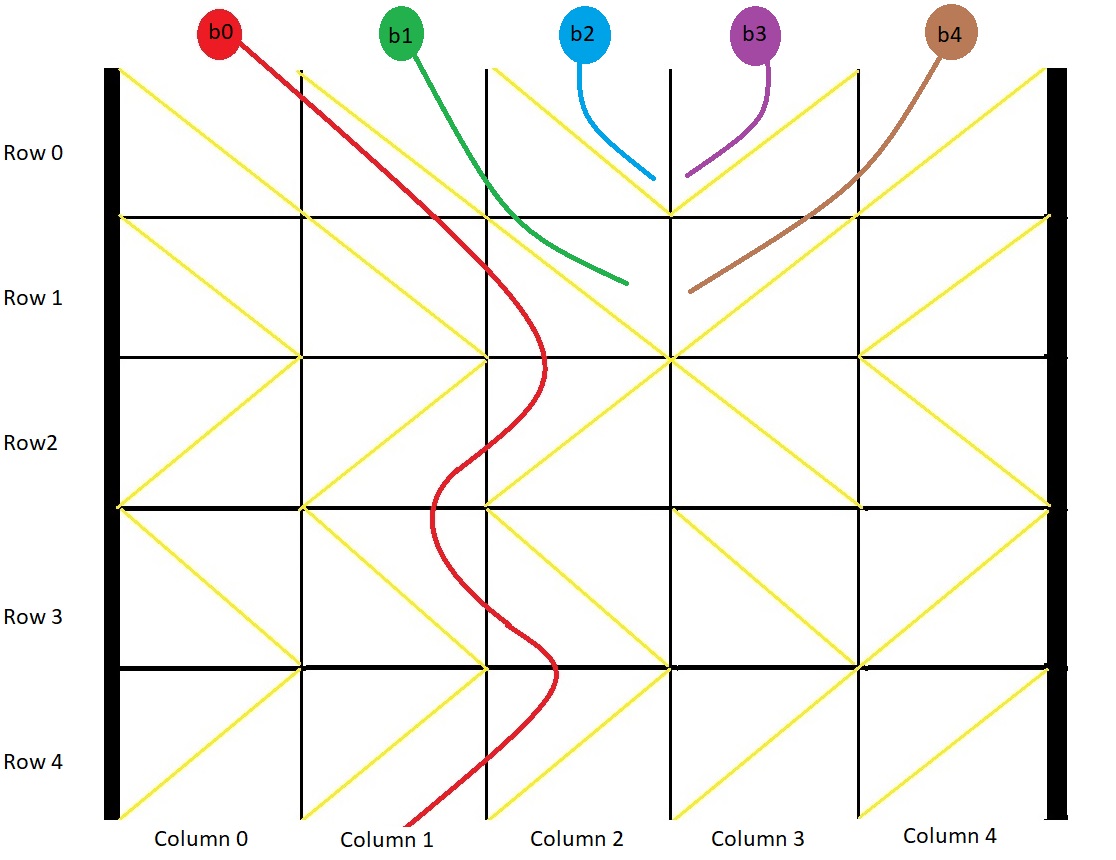
输入：grid = [[1,1,1,-1,-1],[1,1,1,-1,-1],[-1,-1,-1,1,1],[1,1,1,1,-1],[-1,-1,-1,-1,-1]]
输出：[1,-1,-1,-1,-1]
解释：示例如图：
b0 球开始放在第 0 列上，最终从箱子底部第 1 列掉出。
b1 球开始放在第 1 列上，会卡在第 2、3 列和第 1 行之间的 "V" 形里。
b2 球开始放在第 2 列上，会卡在第 2、3 列和第 0 行之间的 "V" 形里。
b3 球开始放在第 3 列上，会卡在第 2、3 列和第 0 行之间的 "V" 形里。
b4 球开始放在第 4 列上，会卡在第 2、3 列和第 1 行之间的 "V" 形里。

示例 2：

输入：grid = [[-1]]
输出：[-1]
解释：球被卡在箱子左侧边上。

示例 3：

输入：grid = [[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1],[1,1,1,1,1,1],[-1,-1,-1,-1,-1,-1]]
输出：[0,1,2,3,4,-1]

 

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 100
• grid[i][j] 为 1 或 -1

通过代码

高赞题解

解题思路

1. 考虑什么情况卡住

   1. 卡在边缘

      1. 卡左边
         
      2. 卡右边
         

   2. 卡在中间
      
      

2. 没有卡住则可以到达下一层

   1. 左拐
      

   2. 右拐
      

方法一：递归

代码

import java.util.Arrays;

class Solution {
    public int[] findBall(int[][] grid) {
        int row = grid.length;
        int col = grid[0].length;
        int[] ans = new int[col];
        for (int i = 0; i < col; i++) {
            ans[i] = out(grid, row, col, i, 0);
        }
        return ans;
    }

    private int out(int[][] grid, int row, int col, int x, int y) {
        //到达底部
        if (y == row) {
            return x;
        }

        //卡在边缘
        if (x == 0 && grid[y][x] == -1) {
            return -1;
        }
        if (x == col - 1 && grid[y][x] == 1) {
            return -1;
        }

        //卡在中间
        if (grid[y][x] == 1 && grid[y][x + 1] == -1) {
            return -1;
        }
        if (grid[y][x] == -1 && grid[y][x - 1] == 1) {
            return -1;
        }

        //到达下一层
        return out(grid, row, col, x + grid[y][x], y + 1);
    }

}

时间复杂度：$O(mn)$
空间复杂度：$O(n)$

方法二：动态规划

图解：

<,,>

小球从第一层往下掉时，每进入一层的位置都依赖于上一层掉出的位置，使用一个数组记录小球到达每一层的位置。

1. 一开始每个球在进入二维网格前的位置分别是0、1、2、3……n-1；
2. 每经过一层可以得到小球将进入的列，如果小球已经被卡住，则将列置为-1；
3. 循环所有的行，便可得到结果。

我们用 $f(x)$ 表示小球到达第x层时每个小球的下标，$f(0)$代表小球进入网格前的小球下标，我们可以列出如下式子：
$$f(0)=[0,1,2,3,……,n-1]$$
$$f(x) = f(f(x-1))$$

class Solution {
    public int[] findBall(int[][] grid) {
        int row = grid.length;
        int col = grid[0].length;
        int[] ans = new int[col];

        // 默认位置
        for (int i = 0; i < col; i++) {
            ans[i] = i;
        }

        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if (ans[j] == -1) {//忽略卡住的球
                    continue;
                }
                if (grid[i][ans[j]] == 1 && ans[j] + 1 < col && grid[i][ans[j] + 1] == 1) {
                    //右移
                    ans[j]++;
                } else if (grid[i][ans[j]] == -1 && ans[j] - 1 >= 0 && grid[i][ans[j] - 1] == -1) {
                    //左移
                    ans[j]--;
                } else {
                    //卡住
                    ans[j] = -1;
                }
            }
        }
        return ans;
    }
}

时间复杂度：$O(mn)$
空间复杂度：$O(n)$

最后再求个👍，谢谢各位大佬！

统计信息

通过次数	提交次数	AC比率
4525	7661	59.1%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言