1895-最大的幻方(Largest Magic Square)

原文链接: https://leetcode-cn.com/problems/largest-magic-square

英文原文

A k x k magic square is a k x k grid filled with integers such that every row sum, every column sum, and both diagonal sums are all equal. The integers in the magic square do not have to be distinct. Every 1 x 1 grid is trivially a magic square.

Given an m x n integer grid, return the size (i.e., the side length k) of the largest magic square that can be found within this grid.

Example 1:

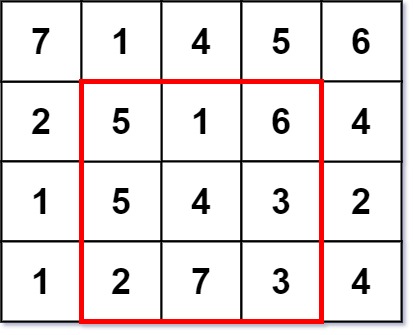
Input: grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
Output: 3
Explanation: The largest magic square has a size of 3.
Every row sum, column sum, and diagonal sum of this magic square is equal to 12.
- Row sums: 5+1+6 = 5+4+3 = 2+7+3 = 12
- Column sums: 5+5+2 = 1+4+7 = 6+3+3 = 12
- Diagonal sums: 5+4+3 = 6+4+2 = 12

Example 2:

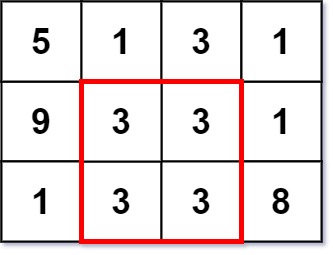
Input: grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]]
Output: 2

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 50
1 <= grid[i][j] <= 10⁶

中文题目

一个 k x k 的幻方指的是一个 k x k 填满整数的方格阵，且每一行、每一列以及两条对角线的和全部相等。幻方中的整数 不需要互不相同 。显然，每个 1 x 1 的方格都是一个幻方。

给你一个 m x n 的整数矩阵 grid ，请你返回矩阵中 最大幻方 的尺寸（即边长 k）。

示例 1：

输入：grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
输出：3
解释：最大幻方尺寸为 3 。
每一行，每一列以及两条对角线的和都等于 12 。
- 每一行的和：5+1+6 = 5+4+3 = 2+7+3 = 12
- 每一列的和：5+5+2 = 1+4+7 = 6+3+3 = 12
- 对角线的和：5+4+3 = 6+4+2 = 12

示例 2：

输入：grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]]
输出：2

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 50
1 <= grid[i][j] <= 10⁶

通过代码

高赞题解

先求每行、每列的前缀和。然后从大到小枚举尺寸 k，找到第一个符合条件的 k，然后返回即可。否则最后返回 1。

一口气撸了四种语言版本的代码 👇

Python3

class Solution:
    def largestMagicSquare(self, grid: List[List[int]]) -> int:
        m, n = len(grid), len(grid[0])
        rowsum = [[0] * (n + 1) for _ in range(m + 1)]
        colsum = [[0] * (n + 1) for _ in range(m + 1)]
        for i in range(1, m + 1):
            for j in range(1, n + 1):
                rowsum[i][j] = rowsum[i][j - 1] + grid[i - 1][j - 1]
                colsum[i][j] = colsum[i - 1][j] + grid[i - 1][j - 1]

        def check(x1, y1, x2, y2):
            val = rowsum[x1 + 1][y2 + 1] - rowsum[x1 + 1][y1]
            for i in range(x1 + 1, x2 + 1):
                if rowsum[i + 1][y2 + 1] - rowsum[i + 1][y1] != val:
                    return False
            for j in range(y1, y2 + 1):
                if colsum[x2 + 1][j + 1] - colsum[x1][j + 1] != val:
                    return False
            s, i, j = 0, x1, y1
            while i <= x2:
                s += grid[i][j]
                i += 1
                j += 1
            if s != val:
                return False
            s, i, j = 0, x1, y2
            while i <= x2:
                s += grid[i][j]
                i += 1
                j -= 1
            if s != val:
                return False
            return True

        for k in range(min(m, n), 1, -1):
            i = 0
            while i + k - 1 < m:
                j = 0
                while j + k - 1 < n:
                    i2, j2 = i + k - 1, j + k - 1
                    if check(i, j, i2, j2):
                        return k
                    j += 1
                i += 1
        return 1

Java

class Solution {
    private int[][] rowsum;
    private int[][] colsum;

    public int largestMagicSquare(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        rowsum = new int[m + 1][n + 1];
        colsum = new int[m + 1][n + 1];
        for (int i = 1; i <= m; ++i) {
            for (int j = 1; j <= n; ++j) {
                rowsum[i][j] = rowsum[i][j - 1] + grid[i - 1][j - 1];
                colsum[i][j] = colsum[i - 1][j] + grid[i - 1][j - 1];
            }
        }
        for (int k = Math.min(m, n); k > 1; --k) {
            for (int i = 0; i + k - 1 < m; ++i) {
                for (int j = 0; j + k - 1 < n; ++j) {
                    int i2 = i + k - 1, j2 = j + k - 1;
                    if (check(grid, i, j, i2, j2)) {
                        return k;
                    }
                }
            }
        }
        return 1;
    }

    private boolean check(int[][] grid, int x1, int y1, int x2, int y2) {
        int val = rowsum[x1 + 1][y2 + 1] - rowsum[x1 + 1][y1];
        for (int i = x1 + 1; i <= x2; ++i) {
            if (rowsum[i + 1][y2 + 1] - rowsum[i + 1][y1] != val) {
                return false;
            }
        }
        for (int j = y1; j <= y2; ++j) {
            if (colsum[x2 + 1][j + 1] - colsum[x1][j + 1] != val) {
                return false;
            }
        }
        int s = 0;
        for (int i = x1, j = y1; i <= x2; ++i, ++j) {
            s += grid[i][j];
        }
        if (s != val) {
            return false;
        }
        s = 0;
        for (int i = x1, j = y2; i <= x2; ++i, --j) {
            s += grid[i][j];
        }
        if (s != val) {
            return false;
        }
        return true;
    }
}

C++

class Solution {
public:
    int largestMagicSquare(vector<vector<int>> &grid) {
        int m = grid.size(), n = grid.size();
        vector<vector<int>> rowsum(m + 1, vector<int>(n + 1));
        vector<vector<int>> colsum(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; ++i)
        {
            for (int j = 1; j <= n; ++j)
            {
                rowsum[i][j] = rowsum[i][j - 1] + grid[i - 1][j - 1];
                colsum[i][j] = colsum[i - 1][j] + grid[i - 1][j - 1];
            }
        }
        for (int k = min(m, n); k > 1; --k)
        {
            for (int i = 0; i + k - 1 < m; ++i)
            {
                for (int j = 0; j + k - 1 < n; ++j)
                {
                    int i2 = i + k - 1, j2 = j + k - 1;
                    if (check(grid, rowsum, colsum, i, j, i2, j2))
                        return k;
                }
            }
        }
        return 1;
    }

    bool check(vector<vector<int>> &grid, vector<vector<int>> &rowsum, vector<vector<int>> &colsum, int x1, int y1, int x2, int y2)
    {
        int val = rowsum[x1 + 1][y2 + 1] - rowsum[x1 + 1][y1];
        for (int i = x1 + 1; i <= x2; ++i)
            if (rowsum[i + 1][y2 + 1] - rowsum[i + 1][y1] != val)
                return false;
        for (int j = y1; j <= y2; ++j)
            if (colsum[x2 + 1][j + 1] - colsum[x1][j + 1] != val)
                return false;
        int s = 0;
        for (int i = x1, j = y1; i <= x2; ++i, ++j)
            s += grid[i][j];
        if (s != val)
            return false;
        s = 0;
        for (int i = x1, j = y2; i <= x2; ++i, --j)
            s += grid[i][j];
        if (s != val)
            return false;
        return true;
    }
};

Go

func largestMagicSquare(grid [][]int) int {
	m, n := len(grid), len(grid[0])
	rowsum := make([][]int, m+1)
	colsum := make([][]int, m+1)
	for i := 0; i <= m; i++ {
		rowsum[i] = make([]int, n+1)
		colsum[i] = make([]int, n+1)
	}
	for i := 1; i < m+1; i++ {
		for j := 1; j < n+1; j++ {
			rowsum[i][j] = rowsum[i][j-1] + grid[i-1][j-1]
			colsum[i][j] = colsum[i-1][j] + grid[i-1][j-1]
		}
	}
	for k := min(m, n); k > 1; k-- {
		for i := 0; i+k-1 < m; i++ {
			for j := 0; j+k-1 < n; j++ {
				i2, j2 := i+k-1, j+k-1
				if check(grid, rowsum, colsum, i, j, i2, j2) {
					return k
				}
			}
		}
	}
	return 1
}

func check(grid, rowsum, colsum [][]int, x1, y1, x2, y2 int) bool {
	val := rowsum[x1+1][y2+1] - rowsum[x1+1][y1]
	for i := x1 + 1; i < x2+1; i++ {
		if rowsum[i+1][y2+1]-rowsum[i+1][y1] != val {
			return false
		}
	}
	for j := y1; j < y2+1; j++ {
		if colsum[x2+1][j+1]-colsum[x1][j+1] != val {
			return false
		}
	}
	s := 0
	for i, j := x1, y1; i <= x2; i, j = i+1, j+1 {
		s += grid[i][j]
	}
	if s != val {
		return false
	}
	s = 0
	for i, j := x1, y2; i <= x2; i, j = i+1, j-1 {
		s += grid[i][j]
	}
	if s != val {
		return false
	}
	return true
}

func min(a, b int) int {
	if a > b {
		return a
	}
	return b
}

欢迎 Star 关注 Doocs 开源社区 leetcode 项目：https://github.com/doocs/leetcode

统计信息

通过次数	提交次数	AC比率
2152	4015	53.6%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途