原文链接: https://leetcode-cn.com/problems/cyclically-rotating-a-grid

英文原文

You are given an m x n integer matrix grid​​​, where m and n are both even integers, and an integer k.

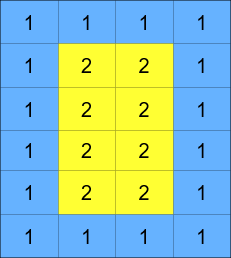
The matrix is composed of several layers, which is shown in the below image, where each color is its own layer:

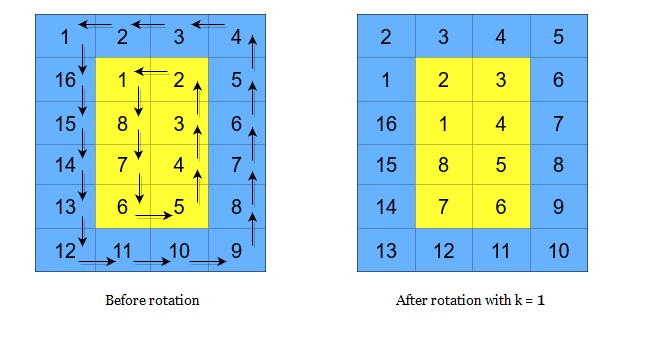
A cyclic rotation of the matrix is done by cyclically rotating each layer in the matrix. To cyclically rotate a layer once, each element in the layer will take the place of the adjacent element in the counter-clockwise direction. An example rotation is shown below:

Return the matrix after applying k cyclic rotations to it.

 

Example 1:

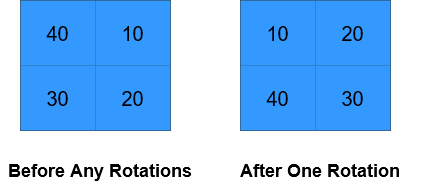
Input: grid = [[40,10],[30,20]], k = 1
Output: [[10,20],[40,30]]
Explanation: The figures above represent the grid at every state.

Example 2:

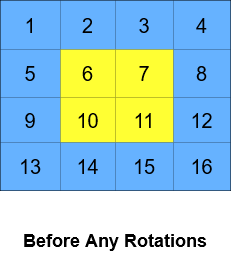
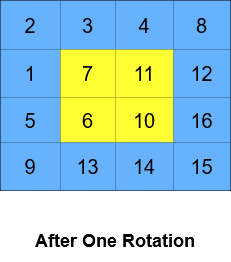
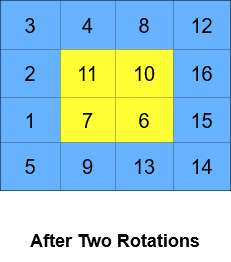
Input: grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], k = 2
Output: [[3,4,8,12],[2,11,10,16],[1,7,6,15],[5,9,13,14]]
Explanation: The figures above represent the grid at every state.

 

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 50
• Both m and n are even integers.
• 1 <= grid[i][j] <= 5000
• 1 <= k <= 109

中文题目

给你一个大小为 m x n 的整数矩阵 grid​​​ ，其中 m 和 n 都是 偶数 ；另给你一个整数 k 。

矩阵由若干层组成，如下图所示，每种颜色代表一层：

矩阵的循环轮转是通过分别循环轮转矩阵中的每一层完成的。在对某一层进行一次循环旋转操作时，层中的每一个元素将会取代其 逆时针 方向的相邻元素。轮转示例如下：

返回执行 k 次循环轮转操作后的矩阵。

 

示例 1：

输入：grid = [[40,10],[30,20]], k = 1
输出：[[10,20],[40,30]]
解释：上图展示了矩阵在执行循环轮转操作时每一步的状态。

示例 2：

输入：grid = [[1,2,3,4],[5,6,7,8],[9,10,11,12],[13,14,15,16]], k = 2
输出：[[3,4,8,12],[2,11,10,16],[1,7,6,15],[5,9,13,14]]
解释：上图展示了矩阵在执行循环轮转操作时每一步的状态。

 

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 50
• m 和 n 都是 偶数
• 1 <= grid[i][j] <= 5000
• 1 <= k <= 109

通过代码

高赞题解

解题思路

我们首先把每一层的元素按顺时针取出来，放到数组 data 中。
然后对 data 旋转 k % (data.length) 次，这里使用队列来简化。
然后再放回去就好了。
具体见程序吧。

代码

class Solution {
    public int[][] rotateGrid(int[][] grid, int k) {
        // 矩阵尺寸
        int m = grid.length, n = grid[0].length;
        // 计算一共有多少层
        int layerNumber = Math.min(m, n) / 2;
        // 逐层处理
        for (int i = 0; i < layerNumber; ++i) {
            // 计算出来当前层需要多大的数组来存放, 计算方法是当前层最大尺寸 - 内部下一层尺寸.
            int[] data = new int[(m - 2 * i) * (n - 2 * i) - (m - (i + 1) * 2) * (n - (i + 1) * 2)];
            int idx = 0;
            // 从左往右
            for (int offset = i; offset < n - i - 1; ++offset)
                data[idx++] = grid[i][offset];
            // 从上往下
            for (int offset = i; offset < m - i - 1; ++offset)
                data[idx++] = grid[offset][n - i - 1];
            // 从右往左
            for (int offset = n - i - 1; offset > i; --offset)
                data[idx++] = grid[m - i - 1][offset];
            // 从下往上
            for (int offset = m - i - 1; offset > i; --offset)
                data[idx++] = grid[offset][i];
            // 把旋转完的放回去
            Integer[] ret = rotateVector(data, k);
            idx = 0;
            // 从左往右
            for (int offset = i; offset < n - i - 1; ++offset)
                grid[i][offset] = ret[idx++];
            // 从上往下
            for (int offset = i; offset < m - i - 1; ++offset)
                grid[offset][n - i - 1] = ret[idx++];
            // 从右往左
            for (int offset = n - i - 1; offset > i; --offset)
                grid[m - i - 1][offset] = ret[idx++];
            // 从下往上
            for (int offset = m - i - 1; offset > i; --offset)
                grid[offset][i] = ret[idx++];
        }
        return grid;
    }

    private Integer[] rotateVector(int[] vector, int offset) {
        // 取余, 否则会有无用功, 超时
        offset = offset % vector.length;
        Deque<Integer> deque = new ArrayDeque<>();
        for (int item : vector) deque.add(item);
        // 旋转操作
        while (offset-- > 0) {
            deque.addLast(deque.pollFirst());
        }
        return deque.toArray(new Integer[0]);
    }
}

统计信息

通过次数	提交次数	AC比率
3348	7526	44.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言