原文链接: https://leetcode-cn.com/problems/maximum-number-of-points-with-cost
英文原文
You are given an m x n integer matrix points (0-indexed). Starting with 0 points, you want to maximize the number of points you can get from the matrix.
To gain points, you must pick one cell in each row. Picking the cell at coordinates (r, c) will add points[r][c] to your score.
However, you will lose points if you pick a cell too far from the cell that you picked in the previous row. For every two adjacent rows r and r + 1 (where 0 <= r < m - 1), picking cells at coordinates (r, c1) and (r + 1, c2) will subtract abs(c1 - c2) from your score.
Return the maximum number of points you can achieve.
abs(x) is defined as:
xforx >= 0.-xforx < 0.
Example 1:
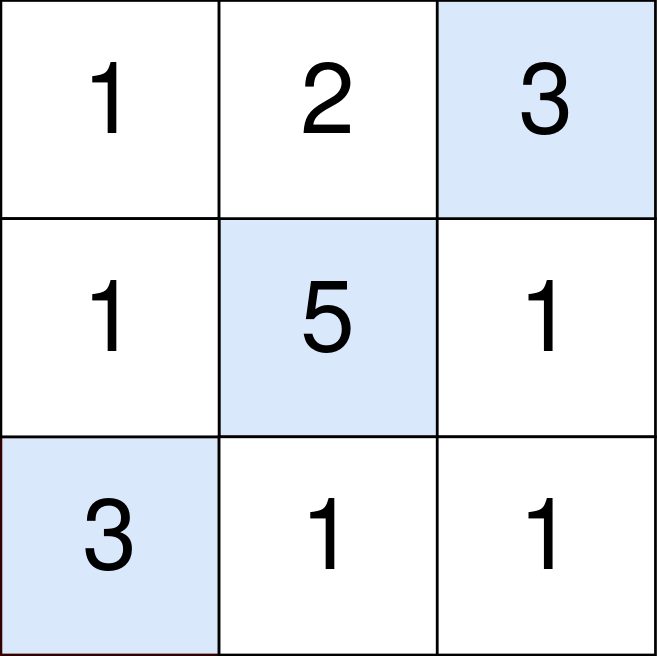
Input: points = [[1,2,3],[1,5,1],[3,1,1]] Output: 9 Explanation: The blue cells denote the optimal cells to pick, which have coordinates (0, 2), (1, 1), and (2, 0). You add 3 + 5 + 3 = 11 to your score. However, you must subtract abs(2 - 1) + abs(1 - 0) = 2 from your score. Your final score is 11 - 2 = 9.
Example 2:
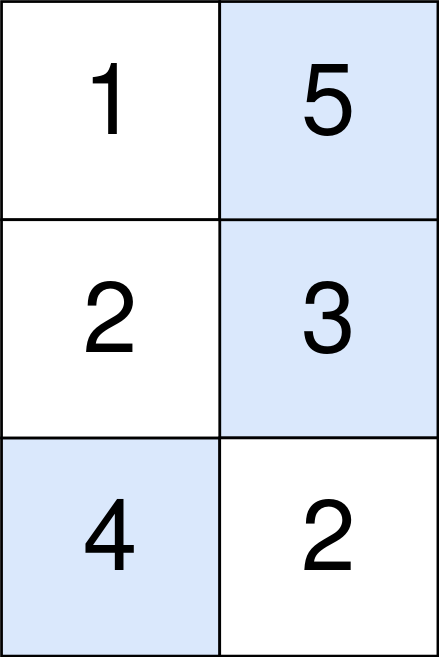
Input: points = [[1,5],[2,3],[4,2]] Output: 11 Explanation: The blue cells denote the optimal cells to pick, which have coordinates (0, 1), (1, 1), and (2, 0). You add 5 + 3 + 4 = 12 to your score. However, you must subtract abs(1 - 1) + abs(1 - 0) = 1 from your score. Your final score is 12 - 1 = 11.
Constraints:
m == points.lengthn == points[r].length1 <= m, n <= 1051 <= m * n <= 1050 <= points[r][c] <= 105
中文题目
给你一个 m x n 的整数矩阵 points (下标从 0 开始)。一开始你的得分为 0 ,你想最大化从矩阵中得到的分数。
你的得分方式为:每一行 中选取一个格子,选中坐标为 (r, c) 的格子会给你的总得分 增加 points[r][c] 。
然而,相邻行之间被选中的格子如果隔得太远,你会失去一些得分。对于相邻行 r 和 r + 1 (其中 0 <= r < m - 1),选中坐标为 (r, c1) 和 (r + 1, c2) 的格子,你的总得分 减少 abs(c1 - c2) 。
请你返回你能得到的 最大 得分。
abs(x) 定义为:
- 如果
x >= 0,那么值为x。 - 如果
x < 0,那么值为-x。
示例 1:

输入:points = [[1,2,3],[1,5,1],[3,1,1]] 输出:9 解释: 蓝色格子是最优方案选中的格子,坐标分别为 (0, 2),(1, 1) 和 (2, 0) 。 你的总得分增加 3 + 5 + 3 = 11 。 但是你的总得分需要扣除 abs(2 - 1) + abs(1 - 0) = 2 。 你的最终得分为 11 - 2 = 9 。
示例 2:

输入:points = [[1,5],[2,3],[4,2]] 输出:11 解释: 蓝色格子是最优方案选中的格子,坐标分别为 (0, 1),(1, 1) 和 (2, 0) 。 你的总得分增加 5 + 3 + 4 = 12 。 但是你的总得分需要扣除 abs(1 - 1) + abs(1 - 0) = 1 。 你的最终得分为 12 - 1 = 11 。
提示:
m == points.lengthn == points[r].length1 <= m, n <= 1051 <= m * n <= 1050 <= points[r][c] <= 105
通过代码
高赞题解
本文用 $n$ 表示行数,$m$ 表示列数。
定义 $f[i][j]$ 表示前 $i$ 行中,第 $i$ 行选择 $\textit{points}[i][j]$ 时的最大得分。通过枚举上一行的转移来源 $k$,我们有
$$
f[i][j] = \textit{points}[i][j] + \max f[i-1][k] - |k-j|
$$
由于转移是 $O(m)$ 的,所以总体复杂度是 $O(nm^2)$ 的,我们需要优化。
拆掉绝对值符号,将上式变形为
$$
f[i][j] =
\begin{cases}
\textit{points}[i][j] + \max f[i-1][k] - (j - k),&k\le j\
\textit{points}[i][j] + \max f[i-1][k] - (k - j),&k > j
\end{cases}
$$
将 $j$ 提出来,化简为
$$
f[i][j] =
\begin{cases}
\textit{points}[i][j] - j + \max f[i-1][k] + k,&k\le j\
\textit{points}[i][j] + j + \max f[i-1][k] - k,&k > j
\end{cases}
$$
由上式可知,在计算 $f[i][j]$ 时,我们需要知道位置 $j$ 左侧的 $f[i-1][k] + k$ 的最大值,以及位置 $j$ 右侧的 $f[i-1][k] - k$ 的最大值。这可以在计算完一整行 $f[i-1][]$ 之后,在计算下一行 $f[i][]$ 之前,预处理出来。
这样优化后,转移就从 $O(m)$ 降为 $O(1)$,于是时间复杂度为 $O(nm)$。
代码实现时,$f$ 的第一维可以压缩掉,且预处理过程可以只处理 $f[i-1][k] - k$ 的最大值,$f[i-1][k] + k$ 的最大值可以一边遍历 $\textit{points}[i][]$ 一边计算。
func maxPoints(points [][]int) int64 {
ans := 0
m := len(points[0])
f := make([][2]int, m)
sufMax := make([]int, m) // 后缀最大值
for i, row := range points {
if i == 0 {
for j, v := range row {
ans = max(ans, v)
f[j][0] = v + j
f[j][1] = v - j
}
} else {
preMax := math.MinInt32
for j, v := range row {
preMax = max(preMax, f[j][0])
res := max(v-j+preMax, v+j+sufMax[j]) // 左侧和右侧的最大值即为选择 points[i][j] 时的计算结果
ans = max(ans, res) // 直接更新答案,这样下面就不直接存储 res 了,改为存储 res + j 和 res - j
f[j][0] = res + j
f[j][1] = res - j
}
}
// 计算完一整行 f 后,对于每个位置 j,计算其右侧的所有 f[k] - k 的最大值
// 这可以通过倒着遍历 f 求出
sufMax[m-1] = f[m-1][1]
for j := m - 2; j >= 0; j-- {
sufMax[j] = max(sufMax[j+1], f[j][1])
}
}
return int64(ans)
}
func max(a, b int) int {
if a > b {
return a
}
return b
}统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 3337 | 13471 | 24.8% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




