原文链接: https://leetcode-cn.com/problems/describe-the-painting

英文原文

There is a long and thin painting that can be represented by a number line. The painting was painted with multiple overlapping segments where each segment was painted with a unique color. You are given a 2D integer array segments, where segments[i] = [starti, endi, colori] represents the half-closed segment [starti, endi) with colori as the color.

The colors in the overlapping segments of the painting were mixed when it was painted. When two or more colors mix, they form a new color that can be represented as a set of mixed colors.

• For example, if colors 2, 4, and 6 are mixed, then the resulting mixed color is {2,4,6}.

For the sake of simplicity, you should only output the sum of the elements in the set rather than the full set.

You want to describe the painting with the minimum number of non-overlapping half-closed segments of these mixed colors. These segments can be represented by the 2D array painting where painting[j] = [leftj, rightj, mixj] describes a half-closed segment [leftj, rightj) with the mixed color sum of mixj.

• For example, the painting created with segments = [[1,4,5],[1,7,7]] can be described by painting = [[1,4,12],[4,7,7]] because:

  <ul>
      <li><code>[1,4)</code> is colored <code>{5,7}</code> (with a sum of <code>12</code>) from both the first and second segments.</li>
      <li><code>[4,7)</code> is colored <code>{7}</code> from only the second segment.</li>
  </ul>
  </li>
  

Return the 2D array painting describing the finished painting (excluding any parts that are not painted). You may return the segments in any order.

A half-closed segment [a, b) is the section of the number line between points a and b including point a and not including point b.

 

Example 1:

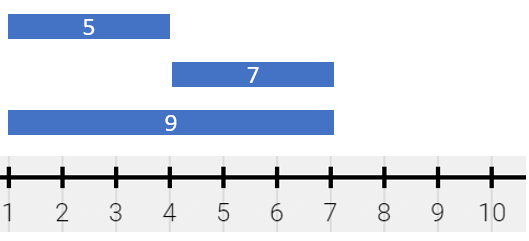
Input: segments = [[1,4,5],[4,7,7],[1,7,9]]
Output: [[1,4,14],[4,7,16]]
Explanation: The painting can be described as follows:
- [1,4) is colored {5,9} (with a sum of 14) from the first and third segments.
- [4,7) is colored {7,9} (with a sum of 16) from the second and third segments.

Example 2:

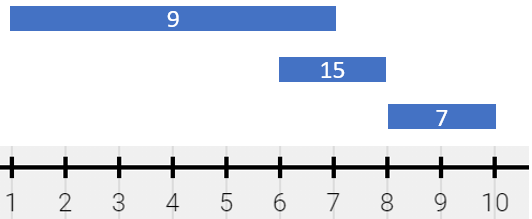
Input: segments = [[1,7,9],[6,8,15],[8,10,7]]
Output: [[1,6,9],[6,7,24],[7,8,15],[8,10,7]]
Explanation: The painting can be described as follows:
- [1,6) is colored 9 from the first segment.
- [6,7) is colored {9,15} (with a sum of 24) from the first and second segments.
- [7,8) is colored 15 from the second segment.
- [8,10) is colored 7 from the third segment.

Example 3:

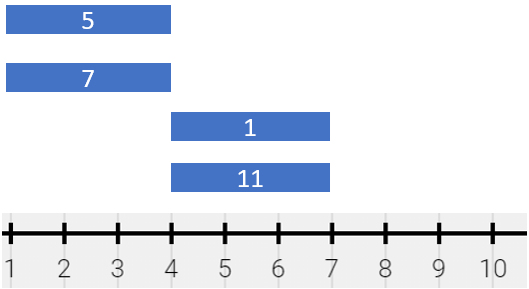
Input: segments = [[1,4,5],[1,4,7],[4,7,1],[4,7,11]]
Output: [[1,4,12],[4,7,12]]
Explanation: The painting can be described as follows:
- [1,4) is colored {5,7} (with a sum of 12) from the first and second segments.
- [4,7) is colored {1,11} (with a sum of 12) from the third and fourth segments.
Note that returning a single segment [1,7) is incorrect because the mixed color sets are different.

 

Constraints:

• 1 <= segments.length <= 2 * 104
• segments[i].length == 3
• 1 <= starti < endi <= 105
• 1 <= colori <= 109
• Each colori is distinct.

中文题目

给你一个细长的画，用数轴表示。这幅画由若干有重叠的线段表示，每个线段有 独一无二 的颜色。给你二维整数数组 segments ，其中 segments[i] = [starti, endi, colori] 表示线段为 半开区间 [starti, endi) 且颜色为 colori 。

线段间重叠部分的颜色会被 混合 。如果有两种或者更多颜色混合时，它们会形成一种新的颜色，用一个 集合 表示这个混合颜色。

• 比方说，如果颜色 2 ，4 和 6 被混合，那么结果颜色为 {2,4,6} 。

为了简化题目，你不需要输出整个集合，只需要用集合中所有元素的 和 来表示颜色集合。

你想要用 最少数目 不重叠 半开区间 来 表示 这幅混合颜色的画。这些线段可以用二维数组 painting 表示，其中 painting[j] = [leftj, rightj, mixj] 表示一个 半开区间[leftj, rightj) 的颜色 和 为 mixj 。

• 比方说，这幅画由 segments = [[1,4,5],[1,7,7]] 组成，那么它可以表示为 painting = [[1,4,12],[4,7,7]] ，因为：

  <ul>
      <li><code>[1,4)</code>&nbsp;由颜色&nbsp;<code>{5,7}</code>&nbsp;组成（和为&nbsp;<code>12</code>），分别来自第一个线段和第二个线段。</li>
      <li><code>[4,7)</code>&nbsp;由颜色 <code>{7}</code>&nbsp;组成，来自第二个线段。</li>
  </ul>
  </li>
  

请你返回二维数组 painting ，它表示最终绘画的结果（没有 被涂色的部分不出现在结果中）。你可以按 任意顺序 返回最终数组的结果。

半开区间 [a, b) 是数轴上点 a 和点 b 之间的部分，包含 点 a 且 不包含 点 b 。

 

示例 1：

输入：segments = [[1,4,5],[4,7,7],[1,7,9]]
输出：[[1,4,14],[4,7,16]]
解释：绘画借故偶可以表示为：
- [1,4) 颜色为 {5,9} （和为 14），分别来自第一和第二个线段。
- [4,7) 颜色为 {7,9} （和为 16），分别来自第二和第三个线段。

示例 2：

输入：segments = [[1,7,9],[6,8,15],[8,10,7]]
输出：[[1,6,9],[6,7,24],[7,8,15],[8,10,7]]
解释：绘画结果可以以表示为：
- [1,6) 颜色为 9 ，来自第一个线段。
- [6,7) 颜色为 {9,15} （和为 24），来自第一和第二个线段。
- [7,8) 颜色为 15 ，来自第二个线段。
- [8,10) 颜色为 7 ，来自第三个线段。

示例 3：

输入：segments = [[1,4,5],[1,4,7],[4,7,1],[4,7,11]]
输出：[[1,4,12],[4,7,12]]
解释：绘画结果可以表示为：
- [1,4) 颜色为 {5,7} （和为 12），分别来自第一和第二个线段。
- [4,7) 颜色为 {1,11} （和为 12），分别来自第三和第四个线段。
注意，只返回一个单独的线段 [1,7) 是不正确的，因为混合颜色的集合不相同。

 

提示：

• 1 <= segments.length <= 2 * 104
• segments[i].length == 3
• 1 <= starti < endi <= 105
• 1 <= colori <= 109
• 每种颜色 colori 互不相同。

通过代码

高赞题解

每一次绘画都会产生一段颜色的变化，只需要在绘画开始的地方记录颜色值增加，结束的地方记录颜色值减少，最后遍历一遍即可完成合并。

#define ll long long
class Solution {
public:
    vector<vector<long long>> splitPainting(vector<vector<int>>& segments) {
        map<int, ll> mp;
        for (const auto& v: segments) {
            int start = v[0], end = v[1], color = v[2];
            mp[start] += color;
            mp[end] -= color;
        }
        vector<vector<ll>> ans;
        ll last = 0, col = 0;
        for (const auto& p: mp) {
            if (col != 0) ans.push_back({last, p.first, col});
            last = p.first;
            col += p.second;
        }
        return ans;
    }
};

统计信息

通过次数	提交次数	AC比率
2009	4867	41.3%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言